Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions in Hindi for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4900]
Click here to view Quantitative Aptitude Questions in English
निर्देश (1-5): निम्नलिखित जानकारी को ध्यान से पढ़ें और दिए गए प्रश्नों के उत्तर दें।
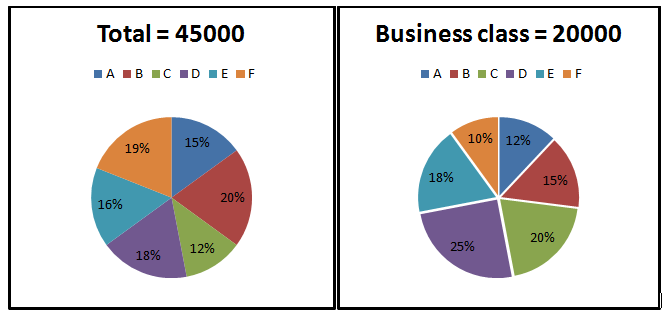
पाई चार्ट 1 तीन शहरों में (बिजनेस क्लास, इकोनॉमी क्लास और प्रीमियम क्लास) से विभिन्न शहरों में बुक किए गए टिकटों की कुल संख्या का प्रतिशत दर्शाता है।
पाई चार्ट 2 विभिन्न शहरों में बुक किए गए बिजनेस क्लास टिकटों की कुल संख्या का प्रतिशत दर्शाता है।
1) मात्रा I: उस शहर में बुक किए गए प्रीमियम क्लास के टिकट ज्ञात कीजिये, जो दिए गए शहरों में बिजनेस क्लास के अलावा बुक किए गए टिकटों की सबसे अधिक संख्या है, अगर इकोनॉमी क्लास और प्रीमियम क्लास का अनुपात 70: 61 है
मात्रा II: दिए गए शहरों में बुक किए गए बिज़नेस क्लास के टिकटों की अधिकतम संख्या ज्ञात करें
a) मात्रा I> मात्रा II
b) मात्रा I < मात्रा II
c) मात्रा I >= मात्रा II
d) मात्रा I <= मात्रा II
e) मात्रा I = मात्रा II (या) संबंध निर्धारित नहीं किया जा सकता है
2) D और F के शहरों में बुक किए गए कुल बिजनेस क्लास के टिकटों और एक ही शहरों में बिजनेस क्लास के अलावा कुल बुक किए गए टिकट के बीच अंतर ज्ञात कीजिये?
a) 2450
b) 2440
c) 2650
d) 2560
e) 2540
3) महिलाओं व पुरुषों की संख्या का अनुपात क्या है जो B और F शहरों में बिजनेस क्लास के टिकटों को एक साथ बुक करते हैं?
कथन I: यदि शहरों में B से F की श्रेणी में बुक की गई महिला वर्ग टिकटों की संख्या का अनुपात 5: 3 है
कथन II: यदि शहरों में B से F के लिए बुक किए गए बिजनेस क्लास टिकट के पुरुषों की संख्या का अनुपात 5: 4 है
a) केवल I
b) केवल II
c) या तो I या II
d) दोनों पर्याप्त नहीं हैं
e) दोनों पर्याप्त हैं
4) शहर A और B में एक साथ बिजनेस क्लास के अलावा बुक किए गए टिकटों की कुल संख्या लगभग सभी शहरों में C और E में बुक किए गए बिजनेस क्लास के टिकटों की कुल संख्या का कितना प्रतिशत है?
a) 152%
b) 124%
c) 104%
d) 136%
e) 183%
5) D और F शहरों में बुक किए गए प्रीमियम क्लास टिकटों की कुल संख्या का अनुपात समान शहरों में बुक किए गए इकोनॉमी क्लास टिकटों की कुल संख्या का अनुपात क्या है?
कथन I: शहर D में बुक किए गए प्रीमियम क्लास के टिकटों की संख्या शहर F में बुक किए गए प्रीमियम क्लास के टिकटों की संख्या से 2050 कम है।
कथन II: शहर F में बुक किए गए इकोनॉमी क्लास के टिकटों की संख्या शहर D में बुक किए गए इकोनॉमी क्लास के टिकटों की संख्या से 1400 अधिक है।
कथन III: शहर F में बुक किए गए प्रीमियम क्लास के टिकटों की संख्या उसी शहर में बुक किए गए इकोनॉमी क्लास के टिकटों की संख्या से 450 कम है।
a) दोनो कथनों में से कोई भी
b) केवल II और III एक साथ
c) केवल I और III एक साथ
d) दोनों विकल्प (b) और (c)
e) सभी कथन पर्याप्त नहीं हैं
निर्देश (6 – 8): निम्नलिखित जानकारी को ध्यानपूर्वक पढ़ें और दिए गए प्रश्नों को उत्तर दें।
अभि, भवन और चार्ली ने क्रमशः रु 40000, रु 60000 और रु 70000 के निवेश के साथ एक व्यवसाय शुरू किया और पहली तिमाही के अंत में, उन्होंने 1: 2: 1 के अनुपात में अतिरिक्त राशि का निवेश किया। दूसरी तिमाही के अंत में, उन्होंने 4: 1: 10 के अनुपात में अतिरिक्त राशि का निवेश किया। तीसरी तिमाही के अंत में, उन्होंने 3: 2: 3 के अनुपात में अतिरिक्त राशि का निवेश किया।
6) अगर दूसरी तिमाही के अंत में अभि और भवन का लाभ अनुपात 9: 14 है, तो चार्ली द्वारा पहली तिमाही के अंत में निवेश की गई अतिरिक्त राशि ज्ञात कीजिए?
a) 15000 रूपये
b) 12000 रूपये
c) 10000 रूपये
d) 16000 रूपये
e) 18000 रूपये
7) अगर अभि द्वारा पहली तिमाही, दूसरी तिमाही और तीसरी तिमाही के अंत में निवेश की गई अतिरिक्त राशि का अनुपात 5: 2: 3 है, तो चार्ली द्वारा निवेश की गई अतिरिक्त राशि का अनुपात ज्ञात कीजिए?
a) 5: 3: 5
b) 3: 5: 5
c) 4: 3: 5
d) 5: 5: 3
e) निर्धारित नहीं किया जा सकता है
8) तीसरी तिमाही के अंत में अभि, भवन और चार्ली का लाभ अनुपात ज्ञात कीजिए?
कथन I: यदि पहली तिमाही के अंत में चार्ली द्वारा निवेश की गई अतिरिक्त राशि और दूसरी तिमाही की राशि समान है।
कथन II: यदि पहली तिमाही के अंत में भवन द्वारा निवेश की गई अतिरिक्त राशि दूसरी तिमाही की तुलना में 1000 रुपये अधिक है।
a) दोनों पर्याप्त हैं
b) दोनों पर्याप्त नहीं हैं
c) या तो I या II
d) केवल II
e) केवल I
9) रवि ने क्रमशः दो स्कीमों A और B में रु ._____ और रु ._____ का निवेश किया। स्कीम A में दो साल के लिए सालाना 10% चक्रवृद्धि ब्याज मिलता है। स्कीम B में 3 साल के लिए 20% साधारण ब्याज मिलता है। स्कीम A में प्राप्त ब्याज रूपये योजना B में प्राप्त ब्याज से 900 कम है
निम्नलिखित में से कौन सा प्रश्नों में दिए गए दो रिक्त को संतुष्ट करता है?
- 10000 रूपये, 5000 रूपये
- 12000 रूपये, 7500 रूपये
- 15000 रूपये, 8000 रूपये
a) केवल I
b) केवल II
c) केवल III
d) दोनों विकल्प a) और c)
e) दोनों विकल्प b) और c)
10) अकेले बिमन 25 दिनों में काम पूरा कर सकते हैं। सोहन की मदद से वह __________ दिनों में काम पूरा कर सकता है। सोहन और मिलन एक साथ 10 दिनों में काम पूरा कर सकते हैं। मिलन अकेले _______________ दिनों में काम पूरा कर सकता है।
निम्नलिखित में से कौन सा प्रश्न में दिए गए दो रिक्त को संतुष्ट करता है?
a) 157/11, 15
b) 10, 30
c) 100/9, 20
d) 12, 25
e) इनमे से कोई नहीं
Answers :
दिशा-निर्देश (1-5):
1) उत्तर: b)
मात्रा I: उस शहर में बुक किए गए प्रीमियम क्लास के टिकट ज्ञात कीजिये, जो दिए गए शहरों में बिजनेस क्लास के अलावा बुक किए गए टिकटों की सबसे अधिक संख्या है, अगर इकोनॉमी क्लास और प्रीमियम क्लास का अनुपात 70: 61 है
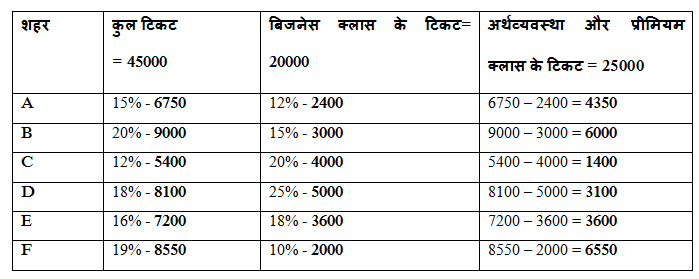
उपरोक्त तालिका से, शहर F ने सबसे अधिक टिकट बिजनेस क्लास के अलावा बुक किए
आवश्यक कुल = 6550 * (61/131) = 3050
मात्रा II: दिए गए शहरों में बुक किए गए बिज़नेस क्लास के टिकटों की उच्चतम संख्या ज्ञात कीजिये।
आवश्यक कुल = 5000 = शहर D
मात्रा I <मात्रा II
2) उत्तर: c)
आवश्यक अंतर = (3100+6550) – (5000+2000)
= 9650 – 7000 = 2650
3) उत्तर: e)
बिज़नेस क्लास के टिकट शहर B में बुक किए गए= (15/100) * 20000
= 3000
बिजनेस क्लास के टिकट F शहर में बुक किए गए हैं= (10/100) * 20000
= 2000
कथन I से,
शहरों में महिलाओं के बुक किए गए बिजनेस क्लास टिकटों की संख्या का अनुपात F = 5x: 3x है
कथन II से,
शहरों में C से F पर बुक किए गए बिजनेस क्लास टिकट के पुरुषों की संख्या का अनुपात= 5y: 4y
कथन I और II से,
शहर C में,
5y + 5x = 3000 —- (1)
शहर में F,
4y + 3x = 2000 —– (2)
समीकरण (1) * 4 – (2) * 5
(20y + 20x) – (20y + 15x) = 12000 – 10000
=> 5x = 2000
=> x = 400
दिए गए प्रश्न को उत्तर देने के लिए दोनों समीकरण एक साथ आवश्यक हैं।
4) उत्तर: d)
एक साथ शहरों A और B में बिजनेस क्लास के अलावा अन्य टिकटों की कुल संख्या
= (4350 + 6000) = 10350
टिकटों की कुल संख्या शहरों C और E में एक साथ बिजनेस क्लास बुक की
= (4000 + 3600) = 7600
आवश्यक प्रतिशत = (10350/7600) * 100 = 136%
5) उत्तर: d)
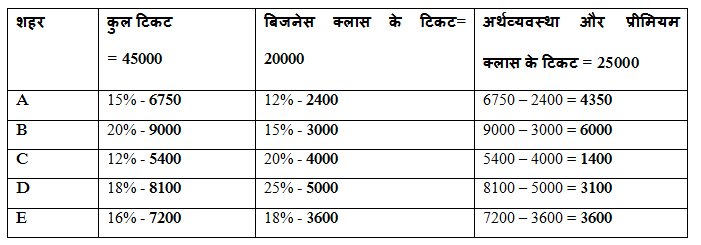
शहर में बुक किए गए प्रीमियम क्लास और इकोनॉमी क्लास के टिकटों की कुल संख्या
= 3100
शहर F में बुक किए गए प्रीमियम क्लास और इकोनॉमी क्लास के टिकटों की कुल संख्या
= 6550
आइए हम शहर में बुक किए गए प्रीमियम क्लास के टिकटों की संख्या लेते हैं क्रमशः D और F x और y हैं।
शहर में बुक किए गए इकॉनोमी क्लास के टिकटों की संख्या क्रमशः (3100-x) और (6550 – y) है।
कथन I से,
शहर में बुक किए गए प्रीमियम क्लास के टिकटों की संख्या शहर F में बुक किए गए प्रीमियम क्लास के टिकटों की संख्या से 2050 कम है।
X = y – 2050
X – y = 2050 —- (1)
कथन II से,
शहर F में बुक किए गए इकॉनोमी क्लास के टिकटों की संख्या शहर D में बुक किए गए इकोनॉमी क्लास के टिकटों की संख्या से 1400 अधिक है।
(6550 – y) = (3100 – x) + 1400
6550 – y = 3100 – x + 1400
2050 = y – x —- (2)
कथन III से,
F शहर में बुक किए गए प्रीमियम क्लास के टिकटों की संख्या उसी शहर में बुक किए गए इकोनॉमी क्लास के टिकटों की संख्या से 450 कम है।
Y = (6550 – Y) – 450
=> 2y = 6100
=> y = 3050
शहर F में बुक किए गए इकोनॉमी क्लास के टिकटों की संख्या = 3050 + 450
= 3500
I और III एक साथ,
शहर F में आरक्षित प्रीमियम श्रेणी के टिकटों की संख्या = 3050
शहर D में बुक किए गए प्रीमियम श्रेणी के टिकटों की संख्या = 3050 – 2050 = 1000
शहर D में बुक किए गए इकॉनोमी क्लास के टिकटों की संख्या = 3100 – 1000 = 2100
शहर F में बुक किए गए इकॉनोमी क्लास के टिकटों की संख्या = 3500
आवश्यक अनुपात = (3050 + 1000): (2100 + 3500)
= 4050: 5600
= 81: 112
II और III से,
शहर F में बुक किए गए इकॉनोमी क्लास के टिकटों की संख्या = 3500
शहर D में बुक किए गए इकॉनोमी क्लास के टिकटों की संख्या = 3500 – 1400
= 2100
शहर में आरक्षित प्रीमियम श्रेणी के टिकटों की संख्या F = 3050
शहर में बुक किए गए प्रीमियम श्रेणी के टिकटों की संख्या D = 3100 – 2100
= 1000
आवश्यक अनुपात = (3050 + 1000): (2100 + 3500)
= 4050: 5600
= 81: 112
इसलिए, कथन I और III एक साथ (या) कथन II और III एक साथ दिए गए प्रश्न को उत्तर देने के लिए पर्याप्त हैं।
Direction (6-8) :
6) उत्तर: c)
आइए अभि, भवन और चार्ली द्वारा निवेशित अतिरिक्त राशि क्रमशः पहली तिमाही के अंत में x, 2x और x लें।
दूसरी तिमाही के अंत में अभि और भवन का लाभ अनुपात
= > (40000*3 + (40000+x)*3): (60000 *3 + (60000+ 2x)*3) = 9/14
(120000 +120000+3x) / (180000+180000+6x) = 9/14
(240000+3x) / (360000+6x) = 9/14
(240000*14+3x*14) = (9*360000+9*6x)
3360000 + 42x = 3240000 + 54x
120000 = 54x – 42x
120000 = 12x
= > x = 10000
पहली तिमाही के अंत में चार्ली द्वारा निवेश की गई अतिरिक्त राशि = रु। 10000
7) उत्तर: d)
पहली तिमाही के अंत में, उन्होंने क्रमशः x, 2x और x अतिरिक्त राशि का निवेश किया
दूसरी तिमाही के अंत में, उन्होंने क्रमशः 4y, y और 10y अतिरिक्त राशि का निवेश किया
तीसरी तिमाही के अंत में, उन्होंने क्रमशः 3z, 2z और 3z अतिरिक्त राशि का निवेश किया
अभि द्वारा पहली तिमाही, दूसरी तिमाही और तीसरी तिमाही के अंत में क्रमशः 5 a, 2 a और 3 a में निवेश की गई अतिरिक्त राशि
5 a = एक्स
चार्ली ने पहली तिमाही (x) = 5a के अंत में अतिरिक्त राशि का निवेश किया
2 a = 4y
a = 2y
y एक / 2 =
चार्ली ने दूसरी तिमाही के अंत में अतिरिक्त राशि का निवेश किया (10y)
= 10 * (a / 2)
= 5 a
3 a = 3z
=> a = z
चार्ली ने तीसरी तिमाही (3z) = 3 a के अंत में अतिरिक्त राशि का निवेश किया
आवश्यक अनुपात = 5a: 5a: 3a = 5: 5: 3
8) उत्तर: a)
पहली तिमाही के अंत में, उन्होंने अतिरिक्त राशि क्रमशः x, 2x और x का निवेश किया
दूसरी तिमाही के अंत में, उन्होंने क्रमशः 4y, y और 10y अतिरिक्त राशि का निवेश किया
कथन I से,
यदि पहली तिमाही के अंत में चार्ली द्वारा निवेश की गई अतिरिक्त राशि और दूसरी तिमाही में समान रूप से
X = 10y —- (1)
कथन II से,
यदि पहली तिमाही के अंत में भवन द्वारा निवेश की गई अतिरिक्त राशि दूसरी तिमाही की तुलना में 1000 रुपये अधिक है
2x – y = 1000 —- (2)
समीकरण समीकरण (1) समीकरण (2) में, हम प्राप्त करते हैं
20y – y = 1000
19y = 1000
Y = 1000/19
X = 10 * (1000/19) = 10000/19
इसलिए, कथन I और II एक साथ दिए गए प्रश्न को उत्तर देने के लिए पर्याप्त हैं।
9) उत्तर: a)
दो साल के शॉर्टकट के लिए चक्रवृद्धि ब्याज,
=> x + x + x2 / 100
=> 10 + 10 + 100/100
=> 21%
आइए हम स्कीम A और B में क्रमशः निवेश करें x और y क्रमशः
योजना A में प्राप्त ब्याज = (21/100) * x
= 21x / 100
योजना B में प्राप्त ब्याज = 3 * (20/100) * y
= 60y / 100
60y / 100 – 21x / 100 = 900
विकल्पों को उपरोक्त स्थिति को पूरा करना चाहिए।
I से,
5000 * (60/100) – (21/100) * 10000 = 900
3000 – 2100 = 900
900 = 900 रु
यह विकल्प दी गई स्थिति को संतुष्ट करता है।
II से,
12000 * (60/100) – 7500 * (21/100) = 900
7200 – 1575 = 900
5625 = 900 रु
यह दी गई स्थिति को संतुष्ट नहीं करता है।
III से,
15000 * (60/100) – 8000 * (21/100) = 900
9000 – 1680 = 900
7320 = 900 रु
यह दी गई स्थिति को संतुष्ट नहीं करता है।
10) उत्तर: c)
विकल्प (A)
1 / मिलन = 1/15
1 / सोहन + 1 / मिलन = 1/10
=> 1 / सोहन + 1/15 = 1/10
=> 1 / सोहन = 1/10 – 1/15
=> 1 / सोहन = (3 – 2) / 30
=> 1 / सोहन = 1/30
बता दें, बिमन और सोहन n दिनों में काम पूरा कर सकते हैं।
n / 25 + n / 30 = 1
=> n x (6 + 5) / 150 = 1
=> n = 150/11 दिन
यह दी गई स्थिति को संतुष्ट नहीं करता है।
विकल्प (B)
1 / मिलन = 1/30
1 / सोहन + 1 / मिलन = 1/10
=> 1 / सोहन + 1/30 = 1/10
=> 1 / सोहन = 1/10 – 1/30
=> 1 / सोहन = (3 – 1) / 30
=> 1 / सोहन = 2/30
=> 1 / सोहन = 1/15
बता दें, बिमन और सोहन n दिनों में काम पूरा कर सकते हैं।
n / 25 + n / 15 = 1
=> n x (3 + 5) / 75 = 1
=> n = 75/8 दिन
यह दी गई स्थिति को संतुष्ट नहीं करता है।
विकल्प (C)
1 / मिलन = 1/20
1 / सोहन + 1 / मिलन = 1/10
=> 1 / सोहन + 1/20 = 1/10
=> 1 / सोहन = 1/10 – 1/20
=> 1 / सोहन = (2 – 1) / 20
=> 1 / सोहन = 1/20
बता दें, बिमन और सोहन n दिनों में काम पूरा कर सकते हैं।
n / 25 + n / 20 = 1
=> n x (4 + 5) / 100 = 1
=> n = 100/9 दिन
यह दी गई स्थिति को संतुष्ट करता है।
विकल्प (d)
1 / मिलन = 1/25
1 / सोहन + 1 / मिलन = 1/10
=> 1 / सोहन + 1/25 = 1/10
=> 1 / सोहन = 1/10 – 1/25
=> 1 / सोहन = (5 – 2) / 50
=> 1 / सोहन = 3/50
बता दें, बिमन और सोहन n दिनों में काम पूरा कर सकते हैं।
n / 25 + 3n / 50 = 1
=> n x (2 + 3) / 50 = 1
=> n = 50/5 = 10 दिन
यह दी गई स्थिति को संतुष्ट नहीं करता है।