Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions in Hindi for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4907]Click here to View Quantitative Aptitude Questions in English
निर्देश (1 – 5): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें:
दिए गए बार ग्राफ वर्ष 2013 – 2017 में एक कंपनी द्वारा निर्मित उत्पादों की संख्या (हजारों में) दिखाता है और लाइन ग्राफ बिना बिके उत्पादों का प्रतिशत दिखाता है।
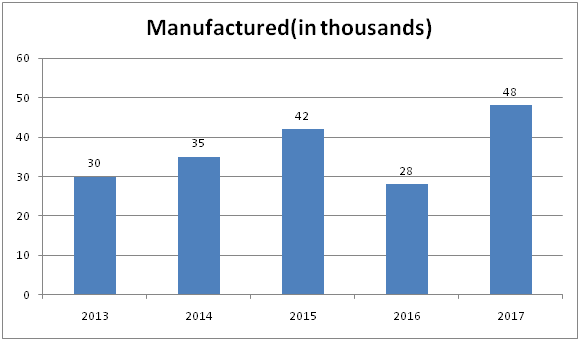
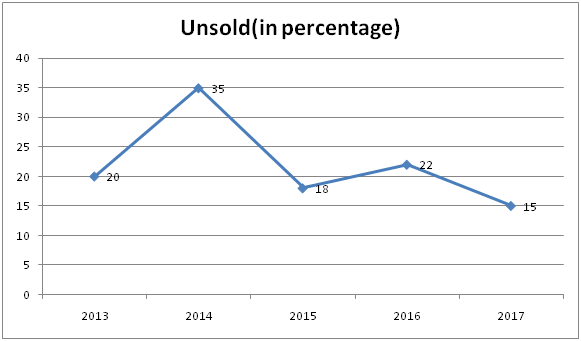
1) 2013 से 2017 के वर्षों में बेचे गए उत्पाद का औसत क्या है?
a) 28766
b) 27866
c) 28966
d) 37866
e) इनमे से कोई नहीं
2) 2017 में कंपनी के गैर-दोषपूर्ण उत्पाद और दोषपूर्ण का अनुपात क्या है?
कथन I: 2017 में कंपनी का दोषपूर्ण उत्पाद वर्ष 2015 में कंपनी के बिना बिके उत्पाद का 80% है।
कथन II: साल 2017 में कंपनी के गैर दोषपूर्ण उत्पाद साल 2013 में निर्मित उत्पाद की संख्या का आधा है।
a) केवल I
b) केवल II
c) या तो I या II पर्याप्त है
d) सभी I और II प्रश्न उत्तर के लिए आवश्यक है
e) प्रश्न सभी I और II के साथ उत्तर नहीं हो सकता है
3) 2018 में कंपनी का बिना बिके उत्पाद कितने है?
मात्रा I: वर्ष 2018 में कंपनी द्वारा निर्मित उत्पादों की संख्या 2016 में निर्मित उत्पाद का 120% है। वर्ष 2018 में बेचे और बिना बिके उत्पाद की संख्या का अनुपात 4: 3 है।
मात्रा II: वर्ष 2018 में बिना बिके उत्पाद की संख्या वर्ष 2014 में दोषपूर्ण उत्पाद की संख्या के बराबर है। और वर्ष 2014 में कंपनी का गैर दोषपूर्ण उत्पाद 2013 में बेचे गए उत्पाद की संख्या का 80% है।
a) मात्रा I > मात्रा II
b) मात्रा I ≥ मात्रा II
c) मात्रा II > मात्रा I
d) मात्रा II ≥ मात्रा I
e) मात्रा I = मात्रा II या संबंध स्थापित नहीं किया जा सकता है
4) 2014 और 2015 में बेचे और बिना बिके उत्पाद के बीच अंतर का योग वर्ष 2013, 2016 और 2017 में बेचे और बिना बिके उत्पाद की कुल संख्या की तुलना में लगभग कितने प्रतिशत अधिक है?
a) 105%
b) 93%
c) 72%
d) 66%
e) 117%
5) कंपनी 2014, 2016 और 2017 में एक साथ निर्मित उत्पादों का औसत क्या है?
a) 35000
b) 39000
c) 37000
d) 34000
e) इनमे से कोई नहीं
Directions (6 – 10): Each question contains a statement followed by मात्रा I, मात्रा II and मात्रा III. Which of the following should be placed in the blank spaces of the expression “मात्रा I__ मात्रा II ___ मात्रा III” from left to right with respect to the above statements?
6) मात्रा I: Ram borrowed the money from Prem at the rate of 12% per annum simple interest. Then Ram deposited that money from the bank of simple interest at 20%. At the end of 18 years, Ram earned the profit of Rs. 540. Find the Sum?
मात्रा II: The CI and SI on a certain sum for two years at the rate of 5 % is Rs.165 and Rs.150 respectively. Find the sum?
मात्रा III: A and B started the business by investing Rs. 4000 and Rs. 2000 respectively. After six months A withdrew Rs. 800. The total profit at the end of a year is Rs. 2800, then find the profit share of B?
a) <, <
b) <, >
c) >, >
d) =, <
e) =, >
7) मात्रा I: अनु ने 10 रूपये, 50 रूपये और 100 रूपये के नोट के रूप में 6200 रूपये हैl इन नोटों की संख्या का अनुपात 7: 5: 3 है। 50 रुपये के नोट की राशि क्या है?
मात्रा II: 2540 रुपये में एक मोबाइल बेचने के बाद अर्जित लाभ, 2326 रूपये में एक मोबाइल बेचने के बाद हानि के बराबर है। मोबाइल की लागत मूल्य क्या है?
मात्रा III: वृत्त और गोले की त्रिज्या का अनुपात 1: 2 है। गोले की घुमावदार सतह का क्षेत्रफल 61600 सेमी है। वृत्त का क्षेत्रफल ज्ञात कीजिए?
a) <, <
b) >, <
c) >, >
d) =, <
e) >, =
8) मात्रा I: वर्ष 2017 में, कोलकाता में पुरुषों और महिलाओं का अनुपात 4: 5 है। वर्ष 2018 में पुरुष जनसंख्या में 20% और महिला जनसंख्या में 10% की वृद्धि हुई। यदि वर्ष 2018 में कुल जनसंख्या 103000 थी, तो वर्ष 2018 में कोलकाता में पुरुष जनसंख्या कितनी है?
मात्रा II: एक डीलर ने 8100 रुपये मर एक सोफा खरीदा। वह अपने अंकित मूल्य पर 10% की छूट देता है और फिर भी 15% प्राप्त करता है। सोफा की अंकित कीमत ज्ञात कीजिये?
मात्रा III: यदि ब्याज की दर में 5% की वृद्धि हुई है, तो साधारण ब्याज में 5 वर्षों के लिए 12000 रुपये की वृद्धि हुई है। यदि बैंक में 10 वर्षों के लिए एक ही राशि जमा की जाती है, तो 10 वर्षों के लिए साधारण ब्याज ज्ञात कीजिये?
a) <, <
b) <, >
c) >, <
d) =, <
e) >, =
9) मात्रा I: यदि राम और सुरेश की वर्तमान आयु का अनुपात 7: 8 है। अब से 10 वर्ष बाद सुरेश और उनकी बहन का अनुपात 3: 2 है। 15 वर्ष के बाद के राम और सुरेश की आयु में अंतर 4 वर्ष है। फिर 7 साल के बाद सुरेश बहन की उम्र क्या होगी?
मात्रा II: x2 – 51x + 650 = 0
मात्रा III: 175 मीटर लंबी ट्रेन एक ही दिशा में चल रही 15 सेकंड में 100 मीटर लंबाई की एक ओर ट्रेन को पार करती है। यदि पहली ट्रेन की गति 90 किमी / घंटा है, तो दूसरी ट्रेन की गति (किमी / घंटा में) ज्ञात करें?
a) <, <
b) ≥, >
c) ≤, >
d) >, <
e) >, =
10) मात्रा I: एक आदमी शांत पानी में 20 किमी प्रति घंटे की गति से तैर सकता है। यदि नदी 12 किमी प्रति घंटे की गति से चल रही है, तो समान दूरी के लिए अनुप्रवाह जाने में 9 घंटे अधिक समय लगता है। दूरी ज्ञात कीजिये?
मात्रा II: दो ट्रेनें A और B एक ही दिशा में क्रमशः 60 किमी प्रति घंटे और x किमी प्रति घंटे की गति से चलती हैं। यदि ट्रेन A ट्रेन B को 20 सेकंड में पार करती है और ट्रेन A और ट्रेन B की लंबाई क्रमशः 80 मीटर और 120 मीटर है। फिर x का मान ज्ञात कीजिए (ट्रेन B एक तेज़ ट्रेन है)?
मात्रा III: एक व्यक्ति ने 9 घंटे में 91 किमी की दूरी तय की। उन्होंने आंशिक रूप से 6 किमी / घंटा पैदल यात्रा की और आंशिक रूप से 12 किमी / घंटा साइकिल पर यात्रा की। फिर आदमी द्वारा पैदल यात्रा की गई दूरी ज्ञात कीजिये।
a) >, >
b) <, <
c) >, <
d) <, >
e) =, >
Answers :
Direction (1-5) :
1) उत्तर: a)
2013 में = (80/100)*30000 = 24000
2014 में = (65/100)*35000 = 22750
2015 में = (82/100)*42000 = 34440
2016 में = (78/100)*28000 = 21840
2017 में = (85/100)*48000 = 40800
औसत = (24000 + 22750 + 34440 + 21840 + 40800)/5 = 28766
2) उत्तर: c)
कथन I से,
2017 में दोषपूर्ण उत्पाद = (80/100) * (18/100) * 42000 = 6048
2017 में गैर दोषपूर्ण उत्पाद = 48000 – 6048 = 41952
आवश्यक अनुपात = 6048: 41952 = 63: 437
कथन II से,
2017 में गैर दोषपूर्ण उत्पाद = 30000/2 = 15000
2017 में दोषपूर्ण उत्पाद = 48000 – 15000 = 33000
आवश्यक अनुपात = 15000: 33000 = 5: 11
या तो I या II प्रश्न के उत्तर के लिए पर्याप्त है।
3) उत्तर: c)
मात्रा I से,
उत्पाद जो 2018 में निर्मित होने जा रहा है = (120/100) * 28000 = 33600
2018 में बिना बिके उत्पाद = (3/7) * 33600 = 14400
मात्रा II से,
वर्ष 2014 में कंपनी का गैर-दोषपूर्ण उत्पाद
में बेचे गए उत्पाद की संख्या => (80/100) * 2013
=> (80/100) * 30000 * (80/100) = 19200
2014 में दोषपूर्ण उत्पाद = 35000 – 19200 = 15800
2018 में बिना बिके उत्पाद = 15800
4) उत्तर: b)
2014 में बेचे और अनसोल्ड उत्पाद का अंतर = (30/100) * 35000 = 10500
2015 में बेचे और बिना बिके उत्पाद का अंतर = (64/100) * 42000 = 26880
योग = 10500 + 26880 = 37380
2017 में बिना बिके उत्पाद = (15/100) * 48000 = 7200
2016 में बिना बिके उत्पाद = (22/100) * 28000 = 6160
2013 में बिना बिके उत्पाद = (20/100) * 30000 = 6000
कुल = 7200 + 6160 + 6000 = 19360
आवश्यक प्रतिशत = [(37380 – 19360)/19360] * 100 = 93%
5) उत्तर: c)
कंपनी 2014, 2016 और 2017 में एक साथ निर्मित उत्पादों का औसत
= (35000 + 28000 + 48000)/3 = 37000
Direction (6-10) :
6) उत्तर: b)
From मात्रा I,
(P*20*18/100) – (P*12*18/100) = 540
P*18*8 = 54000
P = 54000 / (18*8) = Rs. 375
From मात्रा II,
Difference of SI and CI = 165 – 150 = 15
Diff = Sum*(r/100)2
15 = Sum*(5/100)2
(15*100*100)/25 = Sum
Sum = 6000
From मात्रा III,
Profit ratio of A and B = (4000*6 + 3200*6) : (2000*12) = 9 : 5
B’s share = (5/14) * 2800 = Rs. 1000
मात्रा I < मात्रा II > मात्रा III
7) उत्तर: b)
मात्रा I से,
अनुपात = 7x : 5x : 3x
10*7x + 50*5x + 3x*100 = 6200
620x = 6200
X=10
50 रूपये के नोट = 10*5*50 = 2500 रूपये
मात्रा II से,
Profit = Loss
SP1 – CP = CP – SP2
2540 + 2326 = 2CP
CP = (2540 + 2326)/2 = Rs. 2433
मात्रा III से,
4*(22/7)*r*r = 61600
r =70 सेमी
व्रत की त्रिज्या = (½)*70 = 35 सेमी
व्रत का क्षेत्रफल = (22/7)*35*35 = 3850 सेमी 2
मात्रा I > मात्रा II < मात्रा III
8) उत्तर: c)
मात्रा I से
4x*(120/100 + 5x*110/100 =103000
4.8x + 5.5x = 103000
10.3x=103000
X = 10000
पुरुष जनसँख्या = 4*10000*120/100 = 48000
मात्रा II से,
सोफा की बिक्री मूल्य = 8100 * (115/100) = 9315 रूपये
अंकित मूल्य * (90/100) = 9315
सोफा का अंकित मूल्य = 9315*(100/90) = 10350 रूपये
From मात्रा III,
(P*5*(R+5)/100) – (P*5*R/100) =12000
5PR + 25P – 5PR = 120000
25P = 1200000
P = 48000
SI = 48000*10*10/100 = 48000
मात्रा I > मात्रा II < मात्रा III
9) उत्तर: c)
मात्रा I से,
राम की वर्तमान आयु = .x
सुरेश की वर्तमान आयु = 8x
सुरेश की बहन की वर्तमान आयु = y
अंतर = (8x + 15) – (7x + 15) = 4
X = 4 साल
सुरेश की उम्र = 8 * 4 = 32
10 वर्ष के बाद आयु = 32 + 10 = 42 वर्ष
सुरेश की बहन की आयु 10 वर्ष के बाद = (2/3) * 42 = 28 वर्ष
सुरेश की बहन की आयु 7 वर्ष के बाद = 28 – 3 = 25 वर्ष
मात्रा II से,
X2 – 51y + 650 = 0
(x – 26) (x – 25) = 0
X = 26, 25
मात्रा III से,
T = D / S
प्रश्न के अनुसार,
15 = (175 + 100) / [(90 – x) * (5/18)]
15 * [(90 – x) * (5/18)] = 275
[(90 – x) * (5/18)] = 275/15(90 – x) = (275/15) * (18/5)
90 – x = 66
X = 24 किमी / घंटा
दूसरी ट्रेन की गति = 24 किमी / घंटा
मात्रा I ≤ मात्रा II > मात्रा III
10) उत्तर: e)
मात्रा I से,
d/(20 – 12) – d/(20 + 12) = 9
d/8 – d/32 = 9
3d/32 = 9
d = 32*3 = 96 किमी
मात्रा II से,
200 = (x – 60)*5/18*20
36= (x – 60)
X= 96 किमी / घंटा
मात्रा III से,
बता दें कि पैदल यात्रा की दूरी x किमी
फिर साइकिल की दूरी तय की = (91 – x) किमी
अभी , (x/6) + ((91 – x)/12) = 9
(2x + 91 – x)/12 = 9
(X + 91)/12 = 9
X + 91 = 108
X = 17 किमी
मात्रा I = मात्रा II > मात्रा III