Take Free Numerical Ability Sectional Test of 35 Questions as like in the real exam to analyze your preparation level. Our Sectional Test Questions are taken as per the latest exam pattern and so it will be really useful for you to crack the prelims exam lucratively. Students who are weak in Reasoning Ability should utilize this chance constructively to accomplish a successful profession in Banking Field.
[WpProQuiz 4248]Click Here for IBPS Clerk Prelims 2018 High-Quality Mocks
Directions (Q. 1 – 5): Find the wrong term in the following number series?
1) 16830, 1530, 10710, 2140, 6426, 3213
a) 1530
b) 10710
c) 6426
d) 3213
e) 2140
2) 35560, 17781, 5929, 1487.5, 304.5
a) 17781
b) 1487.5
c) 5929
d) 304.5
e) 35560
3) 1142, 1170, 1235, 1360, 1578, 1922
a) 1360
b) 1170
c) 1235
d) 1578
e) 1922
4) 35, 147, 262, 385, 537, 769
a) 537
b) 385
c) 769
d) 147
e) 262
5) 81, 1000, 121, 1727, 169, 2744
a) 81
b) 121
c) 1727
d) 169
e) 2744
Directions (6-10): Study the following information to give the answer of the following questions.
The line graph shows the profit earned by a company over the year
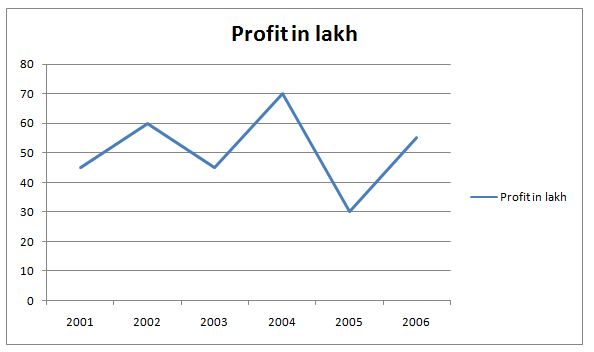
6) What is the profit percent of the company in year 2002, if the income of the company was Rs. 160 lakhs?
a) 80 %
b) 60 %
c) 100 %
d) 40 %
e) None of these
7) What is the approximate percent increase in the profit of the company in the year 2004 while comparing with the previous year?
a) 56 %
b) 52 %
c) 59 %
d) 67 %
e) 44 %
8) What is the approximate average (in lakhs) profit made by the company over the year?
a) 45
b) 51
c) 46
d) 57
e) None of these
9) What is the ratio between the profit earned by company in 2005 and 2003?
a) 3 : 2
b) 5 : 3
c) 2 : 3
d) 3 : 5
e) None of these
10) The expenditure of the company in 2006 was 40 lakhs. What is the ratio of income to the expenditure of the company in that year?
a) 8 : 13
b) 19 : 8
c) 5 : 7
d) 13 : 9
e) None of these
11) A, B and C invested capitals in the ratio 6 : 4 : 9. At the end of year they received the profits in the ratio 4 : 2 : 3. Find the ratio of time for which they contribute the capitals?
a) 4 : 2 : 3
b) 4 : 3 : 2
c) 5 : 2 : 3
d) 4 : 7 : 3
e) None of these
12) A man sold an article at loss of 15%. If it was sold at Rs. 102 more, there would have been a gain of 2 %. Find the cost price of the article?
a) Rs. 650
b) Rs. 700
c) Rs. 600
d) Rs. 800
e) None of these
13) Divide Rs. 960 among A, B and C such that A gets 2/3 of what B gets and B gets 1/5 of what C gets. Find the share of B?
a) Rs. 144
b) Rs. 196
c) Rs. 248
d) Rs. 112
e) None of these
14) A merchant purchase some banana. He purchased 4 bananas for Rs 5. He sold 5 banana for Rs 8. Find the profit percent in the whole transaction.
a) 30
b) 26
c) 32
d) 28
e) None of these
15) A man spends 40 percent of his income. His income increased by 25 percent and his expenditure also increased by 16 percent. Find the percentage increase in his saving?
a) 26
b) 19
c) 21
d) 31
e) None of these
16) Two trains 160 and 120 m long, while going in the same direction the faster train takes one minute and 10 second to pass the other completely. If they are moving in opposite direction, they pass each other completely in 7 second. Find the speed of the trains?
a) 24 m/s and 18 m/s
b) 22 m/s and 18 m/s
c) 20 m/s and 18 m/s
d) 22 m/s and 26 m/s
e) None of these
17) Sudhir can row a 42 km distance downstream in 3 hours and return the same distance in 7 hours. If the stream flows at the rate of 4 km/hr. Find the speed of sudhir in still water?
a) 4 km/hr
b) 10 km/hr
c) 6 km/hr
d) 8 km/hr
e) None of these
18) The income of Sachin and Rahul is in the ratio 11 : 6 and their expenditure is in the ratio of 5 : 2. If each saves Rs. 2000, then find their incomes?
a) Rs. 8250 and Rs. 4500
b) Rs. 8150 and Rs. 3750
c) Rs. 8300 and Rs. 3500
d) Rs. 8200 and Rs. 3950
e) None of these
19) How many different ways can the letter of the word AEROPLANE be arranged so that all the Consonants should not be together?
a) 87120
b) 86520
c) 52840
d) 86140
e) None of these
20) A woman get Rs 800 at the end of first year and Rs 856 at the end of second year on a certain amount of deposited at compound interest. Find the rate of interest?
a) 6
b) 5
c) 7
d) 8
e) 11
Directions (Q. 21 – 30) Find out the approximate value of the following questions.
21) 39.925% of 4335 + 59.784 % of 510 = ? + 432
a) 388
b) 191
c) 357
d) 219
e) 421
22) 59.88 * 14.56 + 517 + 12.812 * 17 = ?
a) 1638
b) 1428
c) 1952
d) 1548
e) 1708
23) 43126.92 ÷ 21953.55 + 522.834 + 12% of 1600 = ?
a) 527
b) 817
c) 747
d) 717
e) 857
24) (814.85 – 79.21 – (9.01)2 ÷ 3.13) % of 1198.98 = ? – 13.94
a) 8522
b) 8400
c) 8152
d) 2142
e) 7850
25) 22.22% of 54 + 62.50% of 783.96 + 120.88 * 11.02 = ?
a) 1750
b) 923
c) 1837
d) 1700
e) 2200
26) 2? * √226 – 930.22 = 246.88/7.99 + 930.05
a) 4
b) 9
c) 7
d) 10
e) 0
27) ? % of (139.89 * 8.01 – 679.96) = 329.92
a) 66
b) 75
c) 35
d) 25
e) None of these
28) 26.98 * 5.22 * (144.92 / 29.21) – (11.91 * 4.04) + 126.83 – 28.84 = ?
a) 725
b) 800
c) 765
d) 705
e) 783
29) 36.81 – ? = 1626.11 + 47.25 – 26.93 * 32.01 – 46.79 * 4.12
a) 584
b) – 516
c) 226
d) -584
e) 336
30) 25.12% of 974.89 + 34.99% of 674.95 = ? – 869.09
a) 1189
b) 1349
c) 1250
d) 1330
e) 1198
Directions (Q. 31 – 35): In each of these questions two equations (I) and (II) are given. You have to solve both the equations and give answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or no relation can be established between x and y
31)
I) X2 – 15x + 56 = 0
II) 2y2– 17y + 36 = 0
32)
I) X2 – 169 = 0
II) Y – √169 = 0
33)
I) 2x2 – 19x + 44 = 0
II) 3y2 + 20y + 25 = 0
34)
I) 2x2 -21x + 55 = 0
II) 6y2 –y – 7 = 0
35)
I) 8x2 – 49x + 45 = 0
II) 7y2 – 23y + 18 = 0
Answers:
Directions (1-5):
1) Answer: e)
The correct series is,
16830, 1530, 10710, 2142, 6426, 3213
The pattern is, ÷ 11, *7, ÷ 5, *3, ÷ 2, (Prime no’s)
The wrong term is, 2140
2) Answer: c)
The correct series is,
35560, 17781, 5930, 1487.5, 304.5
The pattern is, ÷ 2 +1, ÷ 3 +3, ÷ 4 +5, ÷ 5 +7,
The wrong term is, 5929
3) Answer: a)
The correct series is,
1142, 1170, 1235, 1361, 1578, 1922
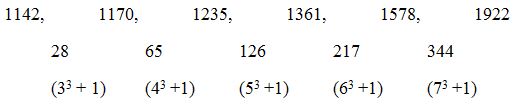
The difference is, 33 +1, 43 +1, 53 +1, 63 +1, 73 +1
The wrong term is, 1360
4) Answer: b)
The correct series is,
35, 147, 262, 386, 537, 769
112 115 124 151 232
3 9 27 81
The difference of difference is, *3
The wrong term is, 385
5) Answer: c)
The correct series is,
81, 1000, 121, 1728, 169, 2744
The pattern is, 92, 103, 112, 123, 132, 143,
The wrong term is, 1727
Directions (6-10):
6) Answer: b)
Income = Expenditure + Profit
Profit percent of the company in year 2002
= > (60 * 100) / 100 = 60 %
7) Answer: a)
Increase % = (25 * 100) / 45 = 55.55 = 56 %
8) Answer: b)
Average = (45 + 60 + 45 + 70 + 30 + 55) / 6
= 50.833
9) Answer: c)
Required ratio = 30 : 45 = 2 : 3
10) Answer: b)
Income = 40 + 55 = 95
Required ratio = 95 : 40 = 19 : 8
11) Answer: b)
TA : TB : TC = (4/6) : (2/4) : (3/9)
TA : TB : TC = 4 : 3 : 2
12) Answer: c)
Let the CP of the article be 100,
S.P = 85
To gain profit of 2 percent S.P = 187
According to the question,
(102/17) * 100 = Rs. 600
13) Answer: a)
Let B get the amount = x
A = 2x/3
C = 5x
According to the question,
(2x/3) + x + 5x = 960
X = 144
Thus the amount of B = Rs. 144
14) Answer: d)
Cost of one banana = 5/4
Selling price of one banana = 8/5
Profit % = ((8/5 – 5/4) * 100)/ (5/4) = 28 %
15) Answer: d)
Let the income of the man is 1000
His expenditure =400
Thus his saving
= > 1000 – 400 = 600
His increased income= 1250
Expenditure= 464
New saving = 1250 – 464 = 786
Percentage increase in saving
= > (186/600) * 100 = 31 %
16) Answer: b)
Let the speed of train be x and y m/s
According to the question,
Difference between the speeds of the train
= > 280/70 = 4 m/s = (x – y)
Sum of the speed of both the train
= > 280/7 = 40 m/s = (x + y)
Thus
X = 22 m/s
Y = 18 m/s
17) Answer: b)
Let the speed of sudhir in still water is x km/h and speed of stream is y km/h
According to the question,
42/(x + 4) = 3——- (I)
42/(x – 4) = 7——- (II)
According to the question,
42/(x + 4) + 42/(x – 4) = 10
42x/(x2 – 16) = 5
42x = 5x2 – 80
5x2 – 42x – 80 = 0
By solving the equation, we get,
X = 10
Speed of still water = 10 km/hr
18) Answer: a)
Let the income of Sachin and Rahul is 11x and 6x respectively,
Income – Savings = Expenditure
According to the question,
(11x – 2000)/(6x – 2000) = 5/2
22x – 4000 = 30x – 10000
8x = 6000
X = 750
Thus, the income of Sachin and Rahul is Rs. 8250 and Rs. 4500
19) Answer: a)
Number of ways so that all consonant should not be together
(9!/2!*2!) – (5!*5!)/(2!* 2!)
= 90720 – 3600
= 87120
20) Answer: c)
Interest of 800
= > (856 – 800) = 56
Rate or interest
= > (56/800) * 100 = 7 %
Directions (21-30):
21) Answer: b)
39.925% of4335 + 59.784% of 510 = ? + 432
1734 + 306 – 1849 = ?
191 = ?
22) Answer: a)
59.88 * 14.56 + 517 + 12.812 * 17 = ?
900 + 517 + 221 = ?
1638 = ?
23) Answer: d)
43126.92/21953.55 + 522.834 + 12% of 1600 = ?
2 + 523 + 192 = ?
717 = ?
24) Answer: a)
(814.85 – 79.21 – (9.01)2/3.13)% of 1198.98 = ? – 13.94
(736 – 81/ 3)% of 1200 = ? – 14
709% of 1200 + 14 = ?
8508 + 14 = ?
8522 = ?
25) Answer: c)
22.22% of 54 + 62.50% of 783.96 + 120.88 * 11.02 = ?
12 + 494 + 1331 =?
1837 = ?
26) Answer: c)
2? * √226 – 930.22 = 246.88/7.99 + 930.05
2? * 15 – 930 = 31 + 930
1891/15 = 2?
126 = 2?
? = 7
27) Answer: b)
?% of (139.89 * 8.01 – 679.96) = 329.92
?% of 440 = 330
? = 75
28) Answer: a)
26.98 * 5.22 * (144.92 / 29.21) – (11.91 * 4.04) + 126.83 – 28.84 = ?
27 * 5 * 5 – 48 + 127 – 29 = ?
675 + 127 – 48 – 29 = ?
725 = ?
29) Answer: d)
36.81 – ? = 1626.11 + 47.25 – 26.93 * 32.01 – 46.79 * 4.12
37 – ? = 1673 – 864 – 188
? = -584
30) Answer: b)
25.12% of 974.89 + 34.99% of 674.95 = ? – 869.09
244 + 236 = ? – 869
? = 1349
Directions (31-35):
31) Answer: a)
I) X2 – 15x + 56 = 0
X2 – 8x – 7x + 56 = 0
X(x – 8) – 7(x – 8) = 0
(x – 8) (x – 7) = 0
X = 8, 7
II) 2y2 – 17y + 36 = 0
2y2 – 8y – 9y + 36 = 0
2y(y – 4) – 9(y – 4) = 0
(2y -9)(y – 4) = 0
Y = 4, 9/2
32) Answer: d)
I) X2 – 169 = 0
X = 13, -13
II) Y – √169 = 0
Y = 13
33) Answer: a)
I) 2x2 – 19x + 44 = 0
2x2 – 8x – 11x + 44 = 0
2x(x – 4) – 11(x – 4) = 0
(2x – 11)(x – 4) = 0
X = 4, 11/2
II) 3y2 + 20y + 25 = 0
3y2 + 15y + 5y + 25 = 0
3y(y + 5) + 5(y + 5) = 0
(y + 5)(3y + 5) = 0
Y = -5, -5/3
34) Answer: a)
I) 2x2-21x + 55 = 0
2x2 – 10x – 11x + 55 = 0
2x(x – 5) – 11(x – 5) = 0
(x – 5) (2x – 11) = 0
X = 5, 11/2
II) 6y2 –y – 7 = 0
6y2 – 7y + 6y – 7 = 0
y(6y – 7) + 1(6y – 7) = 0
(y + 1)(6y -7) = 0
Y = -1, 7/6
35) Answer: e)
I) 8x2 – 49x + 45 = 0
8x2 – 40x – 9x + 45 = 0
8x (x – 5) – 9 (x – 5) = 0
(x – 5) (8x – 9) = 0
X = 5, 9/8
II) 7y2 – 23y + 18 = 0
7y2 – 14y – 9y + 18 = 0
7y (y – 2) – 9(y – 2) = 0
(y – 2)(7y – 9) = 0
Y = 2, 9/7
Click Here for IBPS Clerk Prelims 2018 High-Quality Mocks





