Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7429]Data interpretation
Directions (1 – 5): Study the following graph carefully and answer the given questions.
The table shows the number of students participated in different sections from different schools.
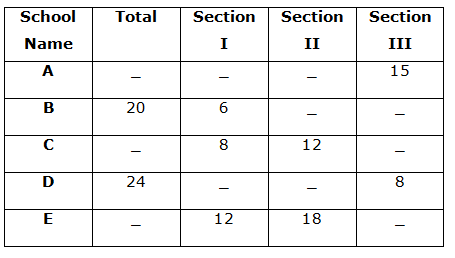1) A group of four students has to form from school C such that the group contains one student in each section and the remaining from any of the section. The number of ways in which this can be possible is 25920. Find the number of students in section III from school C?
a) 15
b) 12
c) 10
d) 20
e) 18
2) A group of two students has to form from school E such that the group contains at least one student in section III. The number of ways in which this can be possible is 195. A committee of five students is to be formed from school E such that the committee contains 2 students from section I, 1 student from section II and 2 students from section III. Find the number of ways in which this can be possible?
a) 15920
b) 16478
c) 23420
d) 17820
e) None of these
3) Find the total number of students in school A?
Statement I: All the students in section II from school A is handshaking with each other and the total number of handshakes is 105.
Statement II: All the students in school A is handshaking with each other and the total number of handshakes is 780.
a) Only I
b) Only II
c) Both I and II
d) Either I or II
e) Neither I nor II
4) In school B, number of students in section III is 75% of the number of students in section II.
Quantity I: In committee P, five students is to be formed from school B such that the committee contains 1 student from each section and the remaining students from any of the section.
Quantity II: In committee Q, five students is to be formed from school B such that committee contains at least one student from section I.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II (or) Relationship cannot be determined
5) A committee of three members is to be formed from each school B and school D. Number of possible ways of a committee contains three students in section III from school D is what percentage of the number of possible ways of committee contains three students in section I from school B?Â
a) 180%
b) 380%
c) 160%
d) 280%
e) None of these
Data Interpretation
Directions (6 – 10): Study the following information carefully and answer the given questions
Three bags A, B and C contains three different coloured balls Red, Blue and Yellow.
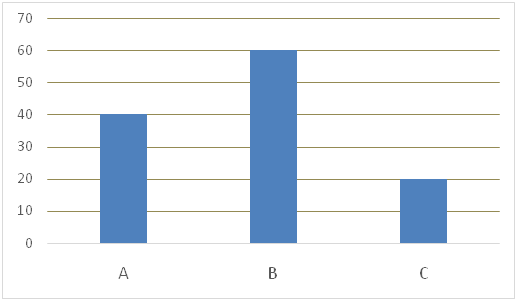
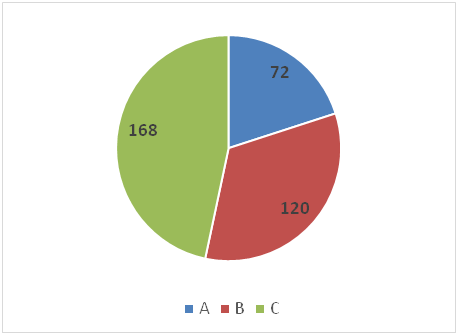
Bar graph given below shows the number of Red colour balls in three different bags A, B and C while the pie chart given below shows the distribution (degree) of Blue colour balls in those three bags.
Some extra information is also given:
When two balls are selected at random from bag A, then probability that one of them is Red and other is Blue is (20/119) and ratio of Blue to Yellow balls in that bag is 3: 5.
When two balls are selected at random from bag B, then probability that both the balls are Blue is (49/447). The difference between the probability of selecting a Blue ball from bag C and the probability of selecting Blue ball from bag B is 1/4.
6) If two balls from bag A, one ball from bag B and one ball from bag C, then what is the probability that both the balls selected from bag A is of Red colour,ball selected from bag B is of Yellow colour and ball selected from bag C is of Blue colour?
a) (8/365)
b) (13/765)
c) (3/65)
d) (10/67)
e) None of these
7) What is the difference between the probability of selecting two Bluecolour balls from bag A and the probability of selecting either ared colour ball or a blue colour ball from bag B?
a) (401/7140)
b) (481/7400)
c) (5903/7400)
d) (4801/7140)
e) None of these
8) The difference between the probabilities of selecting one blue colour ball from bag A and bag B is approximately how much per cent less than the difference between the probabilities of selecting one red colour ball from bag B and bag C?
a) (450/7)%
b) (550/9)%
c) (250/3)%
d) (350/9)%
e) None of these
9) If twoballsare selected at random from each of the bag B and bag C, then what is the probability the both the selected balls are one among the red colour or of blue colour or of yellow colour?
a) (9/16)
b) (93/180)
c) (17/36)
d) (11/36)
e) None of these
10) If ‘p’ number of yellow colour balls from bag C are transferred to bag B and 83(1/3)% of total red colour balls from bag B are transferred to bag C, then the probability of selecting either a red colour ball from bag Bor a blue colour ball from bag C is (11/20), then what is the value of ‘p’.
a) 25
b) 20
c) 10
d) 15
e) None of these
Answers :
Directions (1-5) :
1) Answer: c)
No of students in section III from school C = x
Total number of students in school C = x + 8 + 12 = 20 + x
Number of possible ways = 8C1 * 12C1 * xC1 * (20 + x – 3) C1 = 25920
8 * 12 * x * (17+x) = 25920
17x + x2 = 270
= > x2 + 17x – 270 = 0
= > x2 – 10x + 27x – 270 = 0
= > x (x – 10) + 27 (x – 10) = 0
= > x = 10, – 27 (Eliminate the –Ve value)
Number of students in section III from school C = 10
2) Answer: d)
Number of students in section III from school E = y
Total number of students in school E = (y + 12 + 18)
= y + 30
Number of possible ways = yC1 * 30C1 + yC2 = 195
= > y * 30 + (y*(y-1)/(1 *2)) = 195
= > 30y + (y2 – y)/2 = 195
= > 60y + y2 – y = 390
= > y2 + 59y – 390 = 0
= > y2 + 65y – 6y – 390 = 0
= > y (y + 65) – 6 (y + 65) = 0
= > (y + 65) (y – 6) = 0
= > y = 6, -65 (Eliminate –Ve value)
Total number of students in school E = 30 + 6 = 36
Required number of ways = 12C2 * 18C1 * 6C2
= (12*11 / 1*2) *18 *(6*5 / 1*2)
= 6*11*18*3*5
= 17820
3) Answer: b)
From I,
Number of students in section II from school A = n
Number of handshakes = nC2 = 105
= > [n*(n -1)] / (1 * 2) = 105
= > n2 – n = 210
= > n2 – n – 210 = 0
= > n2 – 15n + 14n – 210 = 0
= > (n – 15) (n – 14) = 0
= > n = 15, -14 (Eliminate –Ve value)
From statement I, We have to find only number of students in section II from school A. We can’t find the total number of students.
Hence, statement I alone is not sufficient to answer the given question.
From II,
Total number of students in school A = x
Number of handshakes = xC2 = 780
= > x * (x – 1)/1*2 = 780
= > x2 – x = 780*2
= > x2 – x – 1560 = 0
= > x2 – 40x + 39x – 1560 = 0
= > x (x – 40) + 39 (x – 40) = 0
= > (x – 40) (x + 39) = 0
= > x = 40, -39 (Eliminate –Ve value)
Total number of students in school A is 40.
Hence, Statement II alone is sufficient to answer the given question.
4) Answer: a)
Number of students in section II from school B = x
Number of students in section III from school B = 75/100 * x
= 3x/4
Total number of students in section II and III from school B = 20 – 6 = 14
= > x + 3x/4 = 14
= > 7x/4 = 14
= > x = 8
Number of students in section III from school B = 8 * 75/100 = 6
Quantity I:
Number of ways = 6C1*8C1*6C1*(20-3)C2
= 6 * 8 * 6 *(17*16/1*2)
= 6*8*6*17*8
= 39168
Quantity II: In committee Q, five students is to be formed from school B such that committee contains at least one student from section I.
Number of ways = 6C1*14C4 + 6C2*14C3 + 6C3*14C2 + 6C4*14C1 + 6C5
= 6006 + 5460 + 1820 + 210 + 6
= 13502
Hence, Quantity I > Quantity II
5) Answer: Â d)
Number of ways in school D = 8C3
= 8*7*6 / 1*2*3 = 56
Number of ways in school B = 6C3
= 6*5*4 / 1*2*3 = 20
Required percentage = (56/20) * 100 = 280%
Directions (6 – 10):
Ratio of number of Blue colour balls in bag A, B and C = 72: 120: 168 = 3: 5: 7
Let number of blue balls in bag A, B and C is 3x, 5x and 7x respectively.
Number of yellow balls in bag A = 3x * (5/3) = 5x
Total balls in bag A = (40 + 3x + 5x) = (40 + 8x)
Probability when two balls are selected from bag A and out of which one Red and other is Blue = [(40C1 * 3xC1)/(40 + 8x)C2] = 20/119
120x/(20 + 4x)(39 + 8x) = 20/119
3x/(5 + x)(39 + 8x) = 2/119
357x = 16x2 + 158x + 390
16x2 – 199x + 390 = 0
16x2 – 160x – 39x + 390 = 0
16x (x – 10) – 39 (x – 10) = 0
(16x – 39) (x – 10) = 0
= > x = 10, 39/16 (Eliminate the fraction value)
x = 10
Number of Blue balls in bag A = 3x = 30
Number of Yellow balls in bag A = 5x = 50
Total balls in bag A = 40 + 30 + 50 = 120
Number of Blue balls in bag B = 5x = 50
Number of Blue balls in bag C = 7x = 70
Let the number of yellow balls in bag B = b
Total balls in bag B = (60 + 50 + b) = (110 + b)
Probability when two Blue balls are selected from bag B = 50C2/(110 + b)C2
= (49/447)
(50 * 49)/[(110 + b)(110 + b – 1)] = 49/447
50/[(110 + b) (109 + b)] = 1/447
22350 = 11990 + 110b + 109b + b2
22350 = 11990 + 219b + b2
b2 + 219b – 10360 = 0
b2 + 259b – 40b – 10360 = 0
(b + 259) (b – 40) = 0
= > b = 40, -259 (Eliminate –ve value)
b = 40
Number of yellow balls in bag B = b = 40
Total balls in bag B = 60 + 50 + 40 = 150
Let the number of yellow balls in bag C = c
Probability of selecting a Blue ball from bag B = 50/150 = 1/3
Total balls in bag C = (20 + 70 + c) = (90 + c)
Probability of selecting a Blue ball from bag C = 70/(90 + c)
According to the question:
[70/(90 + c)] – (1/3) = 1/470/(90 + c) = 7/12
10/(90 + c) = 1/12
120 = 90 + c
c = 30
Number of yellow balls in bag C = c = 30
Total balls in bag C = 20 + 70 + 30 = 120
6) Answer: b)
Probability of selecting two red balls from bag A = 40C2/120C2
= (20 * 39)/(60/119) = (13/119)
Probability of selecting one yellow ball from bag B = 40/150 = (4/15)
Probability of selecting one blue ball from bag C = 70/120 = (7/12)
Required probability = (13/119) * (4/15) * (7/12) = (13/765)
7) Answer: d)
Probability of selecting two Blue colour balls from bag A = 30C2/120C2 = (29/476)
Probability of selecting either a red colour ball or a blue colour ball from bag B
= (60/150) + (50/150) = (11/15)
Required difference = (11/15) – (29/476) = (5236 – 435)/7140
= (4801/7140)
8) Answer: a)
Probability of selecting one blue colour ball from bag A = (30/120) = (1/4)
Probability of selecting one blue colour ball from bag B = (50/150) = (1/3)
Difference = (1/3) – (1/4) = (1/12)
Probability of selecting one red colour ball from bag B = (60/150) = (2/5)
Probability of selecting one red colour ball from bag C = (20/120) = (1/6)
Difference = (2/5) – (1/6) = (7/30)
Required per cent = [{(7/30) – (1/12)}/(7/30)] * 100 = (450/7)%
9) Answer: e)
Probability that both the selected balls from bag B and C are of red colour
= (60/150) * (20/120) = (1/15)
Probability that both the selected balls from bag B and C are of blue colour
= (50/150) * (70/120) = (7/36)
Probability that both the selected balls from bag B and C are of yellow colour
= (40/150) * (30/120) = (1/15)
Total probability = (1/15) + (7/36) + (1/15) = (59/180)
10) Answer: b)
After transfer, number of red colour balls in bag B = 60 – [83(1/3)% of 60]
= 10
After transfer, number of yellow colour balls in bag B = (40 + p)
Total balls in bag B after transfer = 10 + 50 + (40 + p) = (100 + p)
After transfer, number of red colour balls in bag C = 20 + [83(1/3)% of 60]
= 70
After transfer, number of yellow colour balls in bag C = (30 – p)
Total balls in bag C after transfer = 70 + 70 + (30 – p) = (170 – p)
Probability of selecting a red colour ball from bag B = [10/(100 + p)]
Probability of selecting a blue colour ball from bag C = [70/(170 – p)]
According to the question:
[10/(100 + p)] + [70/(170 – p)] = (11/20)20[10(170 – p) + 70(100 + p)] = 11(100 + p)(170 – p)
20[1700 – 10p + 7000 + 70p) = 11(17000 + 70p – p2)
174000 + 1200p = 187000 + 770p – 11p2
11p2 + 430p – 13000 = 0
11p2 – 220p + 650p – 13000 = 0
11p (p – 20) + 650 (p – 20) = 0
= > p = 20, – 650/11 (Eliminate –ve value)
p = 20
