Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for IBPS RRB Clerk Prelims 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
IBPS RRB Clerk Prelims Free Mock Test
Check here for IBPS PO Mock Test 2019
Click Here to Subscribe Crack High Level Puzzles & Seating Arrangement Questions PDF 2019 Plan
[WpProQuiz 6830]Directions (Q. 1 – 5) In the following questions, two equations I and II are given. You have to solve both the equations and give Answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established
1) I) x3 =1331
II) 2y2 -21y +55 =0
2) I) 5x = 7y+21
II) 11x +4y+109 =0
3) I) 2x2 -11x +12 =0
II) 2y2 -17y +36 =0
4) I) 6x2 – 32x + 42 = 0
II) y2 + 7y + 12 = 0
5) I) x2 + 6x + 8 = 0
II) 4y2 – 13y + 9 = 0
Directions (Q. 6 – 10) Study the following information carefully and answer the given questions:
The following table shows the total number of students from various schools playing various different games. Each person is playing only one game 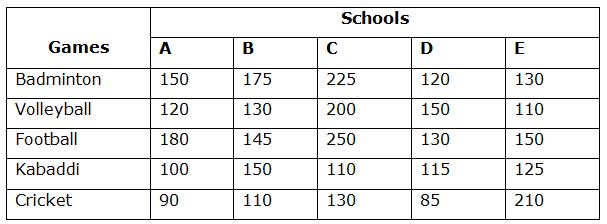
6) Total number of students playing various sports in School A is 32 % of total number of students in School A. Find the total number of students not playing any games in School A?
a) 1480
b) 1620
c) 1360
d) 1570
e) None of these
7) Find the ratio between the total number of students playing Badminton from School A, C and E together to that of total number of students playing Football from School B, C and D together?
a) 56 : 59
b) 41 : 47
c) 33 : 35
d) 101 : 105
e) None of these
8) Find the average number of students playing Kabaddi and Volleyball together from all the Schools together?
a) 710
b) 655
c) 680
d) 620
e) 735
9) Total number of students playing Cricket from School C is approximately what percentage of total number of students playing Football from School C and E together?
a) 45 %
b) 56 %
c) 28 %
d) 33 %
e) 60 %
10) Find the difference between the total number of students playing all the given games together from School B to that of School C?
a) 205
b) 275
c) 310
d) 380
e) None of these
Answers :
Direction (1-5) :
1) Answer: a)
I) x3 =1331
x = ∛1331 =11
II) 2y2 -21y + 55 =0
2y2 -10y -11y +55 =0
2y(y – 5)-11 (y – 5) =0
(2y – 11) (y – 5) =0
y = 11/2, 5
x > y
2) Answer: a)
5x – 7y = 21 —> (1)
11x +4y = -109 –> (2)
By solving the equation (1), (2), we get,
x = -7, y = -8
x > y
3) Answer: d)
I) 2x2 -11x +12 = 0
2x2 – 8x – 3x +12 = 0
2x (x – 4) -3 (x – 4) = 0
(2x – 3) (x – 4) =0
X = 3/2, 4
II) 2y2 -17y +36 = 0
2y2 – 9y – 8y + 36 = 0
y (2y – 9) – 4 (2y – 9) = 0
(y – 4) (2y – 9) =0
y = 4, 9/2
x ≤ y
4) Answer: a)
I) 6x2 – 32x + 42 = 0
6x2 – 18x – 14x + 42 = 0
6x(x – 3)-14 (x – 3) =0
(6x – 14)(x – 3) = 0
x = 3, 7/3
II) y2 + 7y + 12 = 0
(y + 4) (y + 3) = 0
y = -4, -3
x > y
5) Answer: c)
I) x2 + 6x + 8 = 0
(x + 4)(x + 2) = 0
x = -4, -2
II) 4y2 – 13y + 9 = 0
4y2 – 4y – 9y + 9 = 0
4y(y – 1) – 9 (y – 1) =0
(4y – 9) (y – 1) = 0
y = 1, 9/4
x < y
Direction (6-10) :
6) Answer: c)
Total number of students playing various sports in School A
= > 150 + 120 + 180 + 100 + 90 = 640
(32/100)*Total students in School A = 640
Total students in School A = 640*(100/32) = 2000
The total number of students not playing any games in School A
= > 2000*(68/100) = 1360
7) Answer: d)
The total number of students playing Badminton from School A, C and E together
= > 150 + 225 + 130 = 505
The total number of students playing Football from School B, C and D together
= > 145 + 250 + 130 = 525
Required ratio = 505 : 525 = 101 : 105
8) Answer: b)
The total number of students playing Kabaddi and Volleyball together from all the Schools together
= > 100 + 150 + 110 + 115 + 125 + 120 + 130 + 200 + 150 + 110
= > 1310
Required average = 1310/2 = 655
9) Answer: d)
Total number of students playing Cricket from School C = 130
Total number of students playing Football from School C and E together
= > 250 + 150 = 400
Required % = (130/400)*100 = 32.5 % = 33 %
10) Answer: a)
Total number of students playing all the given games together from School B
= > 175 + 130 + 145 + 150 + 110 = 710
Total number of students playing all the given games together from School C
= > 225 + 200 + 250 + 110 + 130 = 915
Required difference = 915 – 710 = 205





