Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
Note: Dear IG ‘ians, Once Again IBPS Guide Team has brought you here with a New Innovative, to make you understand the questions more easier we have started providing Video Solutions for the questions. Practice here & click the link given below to check the video solutions of the same questions. Make use of it & thanks for your love.
[WpProQuiz 4567]Click Below for Video Solutions for these Questions
Directions (1 – 5): Study the following graph carefully and answer the given questions.
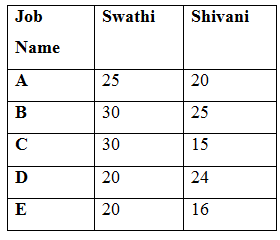
The table shows the number of days taken by Swathi to complete the given percentage of work and the time ratio of Swathi to Shivani to complete the whole work.
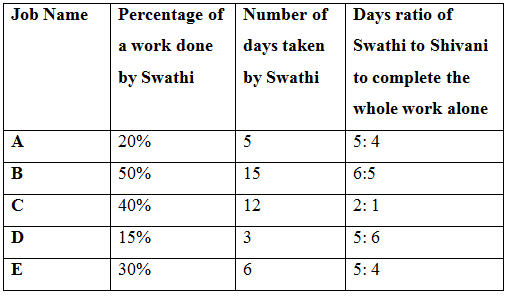
1) Find the number of days taken by Sumaya to complete the Job-C alone?
Statement I: Swathi and Shivani started working to complete Job-C, Sumaya also joins with them to complete the work 4 days before the actual time taken by Swathi and Shivani working together.
Statement II: Swathi started working to complete Job-C with 75% of her original efficiency. After some days Sumaya joins with her and completed Job-C in 30 days. The ratio of the number of days taken by Swathi and Sumaya to complete Job-C is 2 : 1.
a) Only statement I alone is sufficient to answer
b) Only statement II alone is sufficient to answer
c) Either statement I or II alone is sufficient to answer the question
d) Both statements I and II alone are sufficient to answer the question
e) Both statements I and II alone are not sufficient to answer the question
2) Find the total wage to complete Job-B?
Statement I: Swathi and Shivani started working to complete Job-B with their 20% and 25% less than the original efficiency respectively. The ratio of the number of days taken by Swathi and Shivani to complete Job-B is 3 : 4. The difference between their wages is Rs. 300.
Statement II: Shivani started working to complete Job-B. After 6 days swathi also joins with her and increased her efficiency by 20%. Swathi left the work 5 days before the work was completed and get Rs. 8400 as wage.
a) Only statement I alone is sufficient to answer
b) Only statement II alone is sufficient to answer
c) Either statement I or II alone is sufficient to answer the question
d) Both statements I and II alone are sufficient to answer the question
e) Both statements I and II alone are not sufficient to answer the question
3) Find the total number of days taken to complete Job- A?
Statement I: Shivani started working to complete Job-A and after 5 days Janani joins with her. The ratio of the number of days they worked to complete Job-A is 35: 12.
Statement II: Sumi is 25% more efficient than Swathi to complete Job-A. They worked alternatively starting with Sumi to complete Job-A.
a) Only statement I alone is sufficient to answer
b) Only statement II alone is sufficient to answer
c) Either statement I or II alone is sufficient to answer the question
d) Both statements I and II alone are sufficient to answer the question
e) Both statements I and II alone are not sufficient to answer the question
4) Find the number of days taken by Krish alone to complete Job-D?
Statement I: Shivani and Krish started working to complete Job-D and the ratio of the number of days worked by Shivani to Krish is 5: 2.
Statement II: Shivani and Krish completes the Job- B in (375/88) days less than the total number of days taken by Shivani and Swathi working together till the work completed.
a) Only statement I alone is sufficient to answer
b) Only statement II alone is sufficient to answer
c) Either statement I or II alone is sufficient to answer the question
d) Both statements I and II alone are sufficient to answer the question
e) Both statements I and II alone are not sufficient to answer the question
5) What is the efficiency ratio of Janavi to Kamali?
Statement I: Shivani started working to complete Job- C and after 4 days, Janavi joins with him and after few days Janavi replaced by Kamali. The remaining work was completed in 5 days.
Statement II: Janavi and Kamali started working together to complete Job-B and completed the work same as the number of days taken by Shivani and Swathi working together.
a) Only statement I alone is sufficient to answer
b) Only statement II alone is sufficient to answer
c) Either statement I or II alone is sufficient to answer the question
d) Both statements I and II alone are sufficient to answer the question
e) Both statements I and II alone are not sufficient to answer the question
Directions (6 – 10): The questions below are based on the given Series-I. The series-I satisfy a certain pattern, follow the same pattern in Series-II and answer the questions given below.
6)

a) 1288
b) 1326
c) 1498
d) 1452
e) 1374
7)
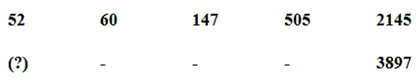
a) 196
b) 125
c) 64
d) 133
e) 156
8)
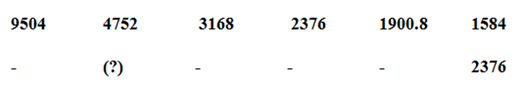
a) 7128
b) 7456
c) 8421
d) 9632
e) 7568
9)
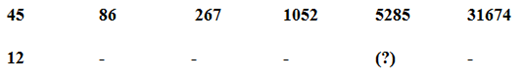
a) 1254
b) 1321
c) 1692
d) 1471
e) 1325
10)
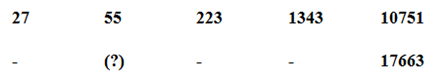
a) 91
b) 84
c) 63
d) 109
e) 87
Click Below for Video Solutions for these Questions
Answers :
Directions (1-5):
Total number of days taken by Swathi to complete Job-A = 5/20*100 = 25 days
Total number of days taken by Shivani to complete Job-A = 25/5 *4 = 20 days
Total number of days taken by Swathi to complete Job-B = 15/50*100 = 30 days
Total number of days taken by Shivani to complete Job-B = 30/6 *5 = 25 days
Total number of days taken by Swathi to complete Job-C = 12/40*100 = 30 days
Total number of days taken by Shivani to complete Job-C = 30/2 *1 = 15 days
Total number of days taken by Swathi to complete Job-D =3/15*100 = 20 days
Total number of days taken by Shivani to complete Job-D = 20/5 *6 = 24 days
Total number of days taken by Swathi to complete Job-E = 6/30*100 = 20 days
Total number of days taken by Shivani to complete Job-E = 20/5 *4 = 16 days
1) Answer: a)
Statement I: Swathi and Shivani started working to complete Job-C, Sumaya also joins with them to complete the work 4 days before the actual time taken by Swathi and Shivani working together.
LCM of 15 and 30 = 30
Total work = 30 units
Swathi = 1 unit
Shivani = 2 units
No. of days taken by Swathi and Shivani working together = 30/(1+2)
= 30/3 = 10 days
No. of days taken by Swathi, Shivani and Sumaya working together= 10 – 4
= 6 days
Swathi, Shivani and Sumaya work per day = 30/6 = 5 units
Sumaya work per day = 5 – 2 – 1 = 2 units
No. of days taken by Sumaya alone to complete the whole work = 30/2 = 15 days
Statement I alone is sufficient to answer the question.
Statement II: Swathi started working to complete Job-C with 75% of her original efficiency. After some days Sumaya joins with her and completed Job-C in 30 days. The ratio of the number of days taken by Swathi and Sumaya to complete Job-C is 2: 1.
Here there is no information about Sumaya’s one day work. From that we cannot answer the given question.
Statement II alone is not sufficient to answer the question.
2) Answer: c)
Statement I: Swathi and Shivani started working to complete Job- B with their 20% and 25% less than the original efficiency respectively. The ratio of the number of days taken by Swathi and Shivani to complete Job-B is 3 : 4. The difference between their wages is Rs. 300
LCM of 25 and 30 = 150
Total work = 150 units
Swathi’s work per day = 5 units
Swathi’s 80% efficiency = 5 * 80/100 = 4 units
Shivani’s work per day = 6 units
Shivani’s 75% efficiency = 6 * 75/100 = 4.5 units
According to the question,
(3x * 4) + (4x*4.5) = 150
12x + 18x = 150
30x =150 => x =5
Number of days worked by Swathi and Shivani is 15 and 20 days respectively.
Swathi’s 15 days work = 4 * 15 = 60 units
Shivani’s 20 days work = 20 * 4.5 = 90 units
Difference between the total units done Shivani and Swathi = 90 – 60 = 30 units
Amount received to complete 30 units of total work = 300
Amount received to complete 150 units of total work = (300/30)*150 = Rs. 1500
Statement II: Shivani started working to complete Job-B. After 6 days swathi also joins with her and increased her efficiency by 20%. Swathi left the work 5 days before the work was completed and get Rs. 8400 as wage.
LCM of 25 and 30 = 150
Total work = 150 units
Shivani’s work per day = 6 units
Swathi’s work per day = 5 units
Swathi’s 120% efficiency = 5 * 120/100 = 6 units
Total number of days worked by Shivani be x and Swathi be (x – 11)
According to the question,
(x * 6) + ((x-11)*6) = 150
6x + 6x – 66 =150
12x = 216
X = 18 days
Total work done by Shivani = 6 * 18 = 108 units
Total work done by Swathi = (18 -11)*6 = 42 units
Amount received by Swathi to complete 42 units is 8400
Total amount to complete 150 units = 8400/42 * 150 = Rs. 30000
3) Answer: b)
Statement I: Shivani started working to complete Job-A and after 5 days Janani joins with her. The ratio of the number of days they worked to complete Job-A is 35: 12.
Here, there is no information about Janani’s individual work. From that we cannot answer the given question.
Statement II: Sumi is 25% more efficient than Swathi to complete Job-A. They worked alternatively starting with Sumi to complete Job-A.
Efficiency ratio of Sumi to Swathi = 125: 100 = 5: 4
Days ratio of Sumi to Swathi = 4: 5
Number of days taken by Sumi alone to complete the whole work = (25/5) * 4
= 20 days
LCM of 25 and 20 = 100
Total work = 100 units
Swathi’s work per day = 100/25 = 4 units
Sumi’s work per day = 100/20 = 5 units
Work done by Swathi and Sumi 2 days = 9 units
Work done by Swathi and Sumi 22 days = 9*11= 99 units
Remaining = 100 – 99 = 1 unit
Required number of days = 22 + 1/5 = 22 (1/5) days
4) Answer: b)
Statement I: Shivani and Krish started working to complete Job-D and the ratio of the number of days worked by Shivani to Krish is 5: 2.
Number of days worked by Shivani and Krish is 5x and 2x respectively.
Here, there is no information about Krish’s individual work. From that we cannot answer the given question.
Statement II: Shivani and Krish completes the Job- B in (375/88) days less than the total number of days taken by Shivani and Swathi working together till the work completed.
LCM of 30 and 25 = 150
Total work = 150 units
Swathi’s per day work = 5 units
Shivani’s per day work = 6 units
Total number of days taken by Swathi and Shivani to complete the whole work
= 150/11 days
Total number of days taken by Shivani and Krish to complete the whole work
= 150/11 – 375/88
= 825/88
Krish one day work = 88/875 – 1/25 = 11/165
Statement II alone is sufficient to answer the given question.
5) Answer: e)
Statement I: Shivani started working to complete Job-C and after 4 days, Janavi joins with him and after few days Janavi replaced by Kamali. The remaining work was completed in 5 days.
From question there is no information about Kamali and Janavi alone to complete the whole work.
Statement I alone is not sufficient to answer the given question.
Statement II: Janavi and Kamali started working together to complete Job-B and completed the work same as the number of days taken by Shivani and Swathi working together.
From question there is no information about Kamali and Janavi alone to complete the whole work.
Statement II alone is not sufficient to answer the given question.
Direction (6-10) :
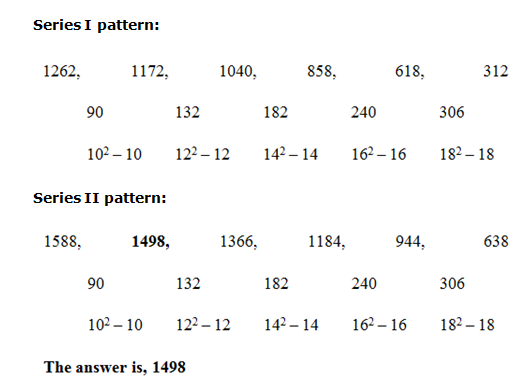
6) Answer: c)
7) Answer: b)
Series I pattern:
52*1 + 23 = 60
60*2 + 33 = 147
147 *3 + 43 = 505
505*4 + 53 = 2145
Series II pattern:
125*1 + 23 = 133
133*2 + 33 = 293
293*3 + 43 = 943
943*4 + 53 = 3897
The answer is, 125
9) Answer: a)
Series I pattern:
9504*(1/2) = 4752
4752*(2/3) = 3168
3168*(3/4) = 2376
2376*(4/5) = 1900.8
1900.8*(5/6) = 1584
Series II pattern:
14256*(1/2) = 7128
7128*(2/3) = 4752
4752*(3/4) = 3564
3564*(4/5) = 2851.2
2851.2*(5/6) = 2376
The answer is, 7128
9) Answer: e)
Series I pattern:
45*2 – 22 = 86
86*3 + 32 = 267
267*4 – 42 = 1052
1052*5 + 52 = 5285
5285*6 – 62 = 31674
Series II pattern:
12*2 – 22 = 20
20*3 + 32 = 69
69*4 – 42 = 260
260*5 + 52 = 1325
1325*6 – 62 = 7914
The answer is, 1325
10) Answer: a)
Series I pattern:
27*2 + 1 = 55
55*4 + 3 = 223
223*6 + 5 = 1343
1343*8 + 7 = 10751
Series II pattern:
45*2 + 1 = 91
91*4 + 3 = 367
367*6 + 5 = 2207
2207*8 + 7 = 17663
The answer is, 91





