Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS Clerk Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS Clerk Prelims Mock Test 2019
[WpProQuiz 7418]
Data Interpretation
Directions (1 – 5): Study the following information carefully and answer the given questions.
In a city, people with 3 types of eye defects (Myopia, Hypermetropia, and Presbyopia) visited different hospitals (Hospital A, Hospital B, Hospital C, Hospital D, and Hospital E). Some people who were having no eye defect also visited the hospitals. The total number of people visiting the hospital is given in the table. The percentage of people who were having Hypermetropia is given in the table along with the ratio of the number of people having Hypermetropia defects to the number of people having no defect. The ratio of the number of people who were having Myopia to the number of people who were having Pyesbyopia is also given in the table. Read the table carefully and answer the following questions.
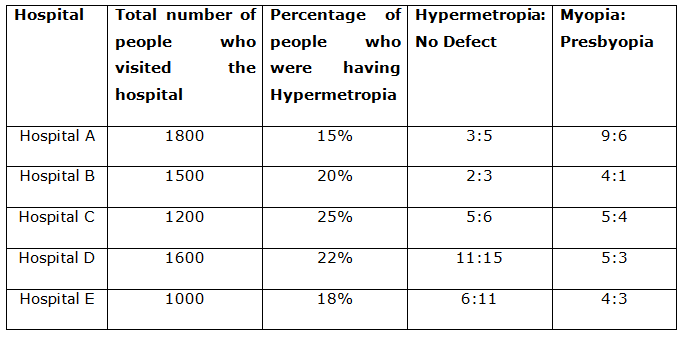
1) Find the total number of people who visited the hospital A and have Myopia.
a) 568
b) 648
c) 658
d) 638
e) 548
2) Find the ratio of the number of people who visited Hospital C and are having Presbyopia to the number of people who visited Hospital D and are having no defect.
a) 1: 2
b) 1: 3
c) 2: 3
d) 3: 4
e) 4: 5
3) Find the total number of people who visited all five Hospitals and have no eye defect.
a) 1070
b) 2050
c) 1970
d) 2070
e) 2270
4) Find the difference between the number of people who visited hospital E and have Myopia than the number of people who visited hospital E and have Presbyopia.
a) 50
b) 60
c) 70
d) 80
e) 90
5) Find the approximate overall percentage of people who visited the given hospital and have a defect of Hypermetropia. (Consider all five hospitals)
a) 12%
b) 16%
c) 18%
d) 20%
e) 22%
Application sums
6) Pipes A, B and C are fitted to a tank. Each pipe can act as either an inlet or outlet pipe. Pipes A, B and C take 4, 6 and 8 hours to fill the empty tank or empty the full tank. In the first hour, pipes A and C act as inlet and B act as outlet. In the second hour, pipes A and B act as inlet and pipe C act as outlet. In the third hour, pipes B and C act as inlet and pipe A act as outlet and the process goes on. When will the tank be filled?
a) In the 5th hour
b) In the 10th hour
c) In the 12th hour
d) In the 15th hour
e) None of these
7) The Senior Executive of the company along with his Executive and Associate invest Rs.40000, Rs.30000 and Rs.50000 respectively in a partnership business for 1 year. The Senior Executive being the senior officer among the three gets one-fifth of the total profit and Executive being second senior officer gets one-tenth of the remaining profit and the remaining profit is divided among the three in the ratio of their investments. If the total profit is Rs.30000, then who will get the minimum share and how much?
a) Senior Executive, Rs.7000
b) Executive, Rs.7800
c) Executive, Rs.8000
d) Associate, Rs.8000
e) None of these
8) Meena’s capital is 2/3 times more than Mira’s capital. Mira invested her capital at 40% per annum for 2 years (compounded annually). At what rate % per annum simple interest should Meena invest her capital so that after 2 years, they both have the same amount of capital?
a) 10%
b) 15.2%
c) 8.8%
d) 20%
e) None of these
9) A box consists of 15 balls numbered from 0 to 14. A boy picked a ball from the box and kept it in the bag after noting its number. He repeated this process 2 more times. What is the probability that the ball picked first by the boy is numbered higher than the ball picked second and the ball picked second by the boy is numbered higher than the ball picked third?
a) 51/3375
b) 67/3375
c) 2197/3375
d) 329/3375
e) None of these
10) In a running race competition involving some boys and girls of an apartment, every member had to play exactly one race with every other member. It was found that in 10 races both the players were boys and in 45 races both the members were girls. Find the number of races in which one member was a boy and other was a girl.
a) 50
b) 40
c) 30
d) 20
e) None of these
Answers :
Directions (1 – 5):
Hospital A:
Total number of people who visited Hospital A = 1800
Percentage of people having Hypermetropia defect (Hospital A) = 15%
Percentage of people with no defect (Hospital A) = 15%*(5/3) = 25%
Percentage of people having Myopia or Presbyopia (Hospital A)
= 100% – (15%+25%) = 100% – 40% = 60%
Percentage of people having Myopia defect (Hospital A) = 60%* {9/(9+6)}
= 60%*(9/15) = 36%
Percentage of people having Presbyopia defect (Hospital A) = 60%*{6/(9+6)}
= 60% * 6/15 = 24%
Similarly calculate the percentage of all the hospitals.
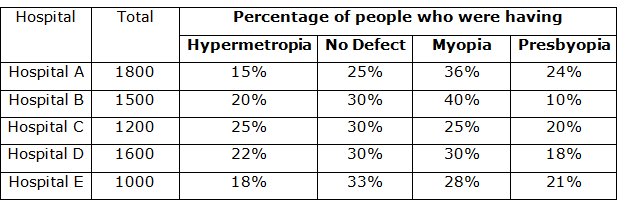
Note:Total number of people who visited the hospital = People having Hypermetropia + People having No defect + People having Myopia + People having Presbyopia
1) Answer: b)
Number of people having Myopia (Hospital A) = 36% of 1800 = 648
2) Answer: a)
Number of people having Presbyopia (Hospital C) = 20% of 1200 = 240
Number of people having no defect (Hospital D) = 30% of 1600 = 480
Required ratio = 240: 480 = 1:2
3) Answer: d)
Number of people how visited Hospital A and have no eye defect
= 25% of 1800 = 450
Number of people how visited Hospital B and have no eye defect
= 30% of 1500 = 450
Number of people how visited Hospital C and have no eye defect
= 30% of 1200 = 360
Number of people how visited Hospital D and have no eye defect
= 30% of 1600 = 480
Number of people how visited Hospital E and have no eye defect
= 33% of 1000 = 330
Therefore, the total number of people who visited all five Hospitals and have no eye defect
= (450+450+360+480+330)
= 2070
4) Answer: c)
Required difference = 1000 * (28% – 21%)
= 1000 * 7/100 = 70
5) Answer: d)
Number of people how visited Hospital A and have Hypermetropia = 15% of 1800
= 270
Number of people how visited Hospital B and have Hypermetropia= 20% of 1500
= 300
Number of people how visited Hospital C and have Hypermetropia= 25% of 1200
= 300
Number of people how visited Hospital D and have Hypermetropia= 22% of 1600
= 352
Number of people how visited Hospital E and have Hypermetropia = 18% of 1000
= 180
Therefore, the total number of people who visited all five Hospitals and have Hypermetropia
= 270+300+300+352+180
= 1402
Total number of people who visited all five hospitals
= 1800+1500+1200+1600+1000 = 7100
Required percentage = (1402/7100)*100 = 20% (Approx.)
Directions (6-10) :
6) Answer: a)
In a cycle of 3 hours, Pipes A, B and C are acting as inlet pipes for 2 hours each and they are acting as outlet pipes for an hour each.
LCM of 4, 6 and 8 = 24
Total = 24 units
A = 6 units per hour
B = 4 units per hour
C = 3 units per hour
Hence, Part of a tank filled in 3 hours (1 cycle) = 2 * (6 + 4 + 3) – (6 + 4 + 3)
= (6 + 4 + 3) = 13
Remaining = 24 – 13 = 11 units
4th hour = 11 – (6 + 3 – 4) = 11 – 5 = 6 units
5th hour pipes can fill 7 units
Thus, tank will be filled in 5th hour.
7) Answer: b)
Ratio of their investments = 40000: 30000: 50000 = 4: 3: 5 — (i)
So, senior executive gets 1/5 * Profit = 1/5 * 30000 = 6000 + his share
Remaining profit = 30000 – 6000 = 24000
Executive gets 1/10 * Remaining profit = 1/10 * 24000 = 2400 + his share
Remaining profit = 24000 – 2400 = 21600
From (i), Senior Executive’s share = 4/12 * 21600 + 6000 = Rs.13200
Executive’s share = 3/12 * 21600 + 2400 = Rs.7800(Minimum share)
Associate’s share = 5/12 * 21600 = Rs.9000
8) Answer: c)
Let the capital of Mira = 3. Then Capital of Meena = 2/3 times more than Mira
Capital of Meena = 2/3 * 3 + 3 = 5
From the given data, we get the below equation.
=> Mira’s capital (1 + r %)n = Meena’s capital + [Meena’s capital * n * R/100]
=> 3(1 + 40/100)2 = 5 + [5 * 2 * R/100]
=> 3 * 140/100 * 140/100 = 5 + 10R/100
=> R = 8.8%
9) Answer: c)
Let the number on the ball picked first = a, second = b, third = c.
The order of a, b and c can be (a>b>c)
Number of ways selecting the first number = 13 (Because we can’t select 0 and 1)
Number of ways selecting the second number = 13 (Because we can’t select 0)
Number of ways selecting the third number = 13 (Because we can’t select first and third number)
Required probability = (13 * 13 * 13)/153
= 2197/3375
10) Answer: a)
Let the number of boys be x and girls be y.
No. of races played between boys = xC2 = 10 = x(x – 1) = 20 => x = 5
Total number of boys participating in running race is 5.
No. of races played between girls = yC2 = 45 = y(y – 1) = 90 => y = 10
Total number of girls participatingin running race is 10.
Therefore, no of running races in which one player is boy and one is girl is,
= 5C1× 10C1= 5 * 10 = 50





