Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7234]
Application sums
1) The ratio of time taken by a boat to cover (x + 4) km in upstream to that of time taken to cover (x + 20) km in still water is 4: 5. If the ratio of speed of boat in downstream to that of stream is 5: 1 and the sum of time taken by the boat to cover (x – 5) km in upstream to that in downstream is 8 hours then find the speed of boat in downstream?
a) 1 km/hr
b) 3 km/hr
c) 4 km/hr
d) 5 km/hr
e) 8 km/hr
2) There are 5 red bikes, “x” blue bikes and “y” black bikes in a showroom. The probability that a blue bike is selected for test drive is 7/24 while the probability that a black bike is selected for test drive is ½. Find the value of (x – y + x * y).
a) 81
b) 79
c) 82
d) 78
e) 83
3) There are two containers P and Q. P contains 56 kg of salt and Q contains 36 kg of sugar. From P 24 kg of salt is taken out and poured into Q. Then 20kg of the mixture from Q is taken out and poured into P. Find the ratio of final quantity of salt to sugar in container P.
a) 10/3
b) 20/3
c) 5/3
d) 2/3
e) 40/3
4) A train X running at the speed of 126 km/hr crosses a man running at 18 km/hr in opposite direction in 12 seconds and crosses a platform ‘’A’’ in 20 seconds. Find the time taken by train Y running at 99 km/hr to cross the platform ‘’B’’. The length of the platform ‘’B’’ is 70 m more than the length of the platform “A” and the length of train Y is equal to the length of train “X”.
a) 24 seconds
b) 28 seconds
c) 36 seconds
d) 32 seconds
e) 22 seconds
5) A, B, and C together can complete a piece of work in 25 days. A and C together can complete 30% of the work in 12 days and B and C together can complete 75% of the work in 33 days. A is 50% more efficient than C. In how many days (approximate integer value) B alone can complete the whole work?
a) 72 days
b) 75 days
c) 79 days
d) 85 days
e) 82 days
Data Interpretation
Direction (6 – 10): Study the following data carefully and answer the questions:
An exam in conducted that consists of three sections: Quant, Reasoning and English. Sectional marked can be calculated as mentioned below:
Sectional marks = 5 * Right answers – 2 * Wrong answers – 0.5 * Un-attempted questions
Normalized marks in any section (If Right answers are > 80%) = 1.2 * Sectional marks
Normalized marks in any section (If Right answers are > 60% and < 80%) = 1 * Sectional marks
Normalized marks in any section (If Right answers are < 60%) = 0.8 * Sectional marks
Total marks in the exam = Normalized marks in Quant + Normalized marks in Reasoning + Normalized marks in English
Total questions in the test are 100 out of which 35 are from Quant section, 35 from Reasoning section and remaining 30 are from English section.
Table given below shows the ratio of number of Right answers to the number of Wrong answers marked by five different students A, B, C, D and E in all the three sections:
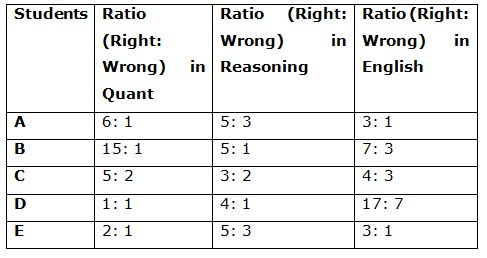6) If student A attempts 80 questions and ratio of attempted questions in Quant, Reasoning and English is 7: 8: 5 respectively, then what is the total marks obtained by him in the test?
a) 252.8
b) 272.9
c) 264.7
d) 246.4
e) None of these
7) If student B left 19 questions in Quant, 23 questions in Reasoning and 20 questions in English un-attempted, then what will be the ratio of sections marks of him in Quant, Reasoning and English respectively?
a) 127: 69: 38
b) 87: 39: 28
c) 27: 9: 13
d) 135: 89: 58
e) None of these
8) If person C attempted, 60% of total quant questions in quant, 71(3/7)% of total questions in Reasoning and 70% of total questions in English, then total right answers are what per cent more than total wrong answers marked by him?
a) 56%
b) 73%
c) 64%
d) 68%
e) None of these
9) Students D marked 15 questions in Quant, 20 questions in reasoning and 17 questions in English correctly, then what will be the ratio of normalized marks obtained by him in Quant, Reasoning and English respectively?
a) 3: 2: 4
b) 1: 3: 2
c) 3: 1: 2
d) 1: 2: 3
e) None of these
10) If the ratio of number of attempted questions by student E in Quant, Reasoning and English is 6: 4: 5 respectively and total marks obtained by him in the test is 147, then how many did he left un-attempted in the test?
a) 50
b) 40
c) 45
d) 75
e) None of these
Answers :
Directions (1-5) :
1) Answer: d)
Let the downstream speed be 5p and speed of stream be p
Then speed of boat in still water will be 5p – p = 4p
And speed of boat in upstream will be 4p – p = 3p
Time taken to cover (x + 4) km in upstream = (x + 4)/3p
And time taken to cover (x + 20) km in still water = (x + 20)/4p
{(x + 4)/3p}: {(x + 20)/4p} = 4: 5
{(x + 4)}/{(3x + 60)} = 1/5
5x + 20 = 3x + 60
x = 20
Also,
The sum of time taken by the boat to cover (x – 5) km in upstream to that in downstream is 8 hours.
(x – 5) = 20 – 5 = 15 km
15/3p + 15/5p = 8
5/p + 3/p = 8
8/p = 8
p = 1 km/hr
The speed of boat in downstream = 5p = 5 * 1 = 5 km/hr
2) Answer: b)
ATQ,
Probability of a blue bike is selected for test drive = x/(5 + x + y) = 7/24
24x = 35 + 7x + 7y
17x – 7y = 35 (equation 1)
Also,
Probability that a black bike is selected for test drive = y/(5 + x + y) = ½
2y = 5 + x + y
x = y – 5
Putting x = y – 5 in equation 1
17(y – 5) – 7y = 35
17y – 85 – 7y = 35
10y = 120
y = 12 and x = 12 – 5 = 7
(x – y + x * y) = 7 – 12 + 7 * 12 = – 5 + 84 = 79
3) Answer: a)
Initially, the Amount of sugar in Q = 36kg
Now, 24kg of salt is poured in Q,
Total quantity in Q becomes = 36kg (sugar) + 24kg (salt) = 60kg (mixture)
The ratio of salt to sugar in Q becomes = 24: 36 = 2: 3
Again, 20kg of the mixture is taken out from Q and poured into P
Therefore, quantity of salt and sugar in P becomes
= {(56 – 24) + 20 * (2/5)} kg of salt + 20 * (3/5) kg of sugar
= (32 + 8) kg of salt + 12 kg of sugar
= 40 kg of salt + 12 kg of sugar
Required ratio = (40/12) = (10/3)
4) Answer: b)
Let the length of train X = x meter
Relative speed of train and man when running in opposite direction = 126 + 18
= 144km/hr = 144 * (5/18) = 40 m/s
ATQ,
40 = x/12
x = 480 m
Let the length of the platform “A” = P1
126 * (5/18) = (P1 + 480)/20
35 = (P1 + 480)/20
P1 + 480 = 700
P1 = 220m
The length of platform “B” = P2 = 220 + 70 = 290
Speed of train Y = 99 km/hr = 99 * (5/18) = 27.5 m/s
Time taken by train Y to cross the platform B = (480 + 290)/27.5
= (770)/27.5 = 28 seconds
5) Answer: c)
Therefore, work of A, B, and C together in one day = 1/25
A and C together can complete 30% of the work in 12 days
100% work will be done in (2/5)*100 = 40 days
Work by A and C together in one day = 1/40
Since A is 50% more efficient than C
Let per day work done by C = x and per day work done by A will be = 150% of x = (150/100)*x = 1.5x
x + 1.5x = 1/40
2.5x = 1/40
x = 1/100
Therefore per day one done by C = 1/100 and
Per day work done by A = 1.5*(1/100) = 1.5/100 = 3/200
Also,
B and C together can complete 75% of the work in 33 days
100% work will be completed in (33/75)*100 = 44 days
Work done by B and C in one day = 1/44
Let the one day work done by B = x
Therefore,
x + 1/100 = 1/44
x = 1/44 – 1/100
x = 7/550
Therefore, days taken by B alone to complete the work = 550/7 = 78.57 (79 approx)
Directions (6 – 10) :
6) Answer: c)
Total attempted questions in Quant = 80 * (7/20) = 28
Total attempted questions in Reasoning = 80 * (8/20) = 32
Total attempted questions in English = 80 * (5/20) = 20
Normalized marks in Quant = 1.2 * [{5 * 28 * (6/7)} – {2 * 28 * (1/7))} – {0.5 * (35 – 28)}] = 130.2
Normalized marks in Reasoning = [{5 * 32 * (5/8)} – {2 * 32 * (3/8))} – {0.5 * (35 – 32)}] = 74.5
Normalized marks in English = [{5 * 20 * (3/4)} – {2 * 20 * (1/4))} – {0.5 * (30 – 20)}] = 60
Total marks in the exam = 130.2 + 74.5 + 60 = 264.7
7) Answer: a)
Attempted questions in Quant = 35 – 19 = 16
Attempted questions in Reasoning = 35 – 23 = 12
Attempted questions in English = 30 – 20 = 10
Sectional marks in Quant = 5 * 16 * (15/16) – 2 * 16 * (1/16) – 0.5 * 19 = 63.5
Sectional marks in Reasoning = 5 * 12 * (5/6) – 2 * 12 * (1/6) – 0.5 * 23 = 34.5
Sectional marks in English = 5 * 10 * (7/10) – 2 * 10 * (3/10) – 0.5 * 20 = 19
Required ratio = 63.5: 34.5: 19 = 127: 69: 38
8) Answer: d)
Total attempted questions in Quant = 60% of 35 = 21
Total attempted questions in Reasoning = 71(3/7)% of 35 = 25
Total attempted questions in English = 70% of 30 = 21
Total right answers marked by him = 21 * (5/7) + 25 * (3/5) + 21 * (4/7) = 15 + 15 + 12 = 42
Total wrong answers marked by him = (21 + 25 + 21) – 42 = 25
Required per cent = [(42 – 25)/25] * 100 = 68%
9) Answer: b)
Normalized marks of D in Quant
= 0.8 * [{5 * 15} – {2 * 15} – {0.5 * (35 – 30)}] = 34
Normalized marks of D in Reasoning
= 1.2 * [{5 * 20} – {2 * 20 * (1/4)} – {0.5 * (35 – 25)}] = 102
Normalized marks of D in English
= [{5 * 17} – {2 * 7} – {0.5 * (30 – 24)}] = 68
Required ratio = 34: 102: 68 = 1: 3: 2
10) Answer: b)
Let number of questions attempted by E in Quant, Reasoning and English is ‘6x’, ‘4x’ and ‘5x’ respectively.
Total un-attempted questions by E = 100 – (6x + 4x + 5x) = (100 – 15x)
Normalized marks in Quant = [5 * 4x – 2 * 2x – 0.5 * (35 – 6x)] = (19x – 17.5)
Normalized marks in Reasoning = [5 * 2.5x – 2 * 1.5x – 0.5 * (35 – 4x)]
= (11.5x – 17.5)
Normalized marks in English = [5 * 3.75x – 2 * 1.25x – 0.5 * (30 – 5x)]
= (18.75x – 15)
Total marks in the test = (19x – 17.5) + (11.5x – 17.5) + (18.75x – 15) = 147
49.25x = 147 + 50
x = 4
Total un-attempted questions by E = (100 – 15x) = 40
