Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7408]Directions (1 – 5): Read the following information carefully and answer the given questions
In a class of 321 students 321 stationary items are distributed such that every student gets exactly 1 item. There are six different items that are distributed among these students namely Pen, Pencil, Erase, Scale, Note and Sharpener. The following line – graph provides information about the number of students who received Pen, Pencil, Erase, Scale, Note and Sharpener.
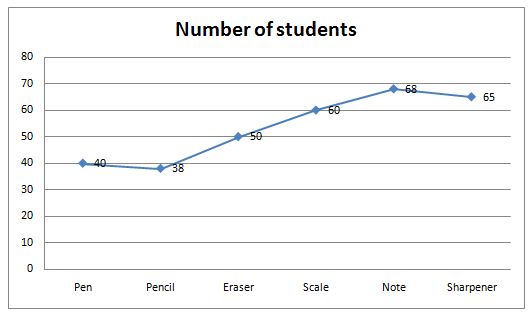
The students exchanged the items among themselves and after they stopped further exchanging, it was noted that no student had the same item that he/she had earlier. Even after the exchange every students has exactly one item.
Among the students that originally had pen, the number of students now having Pencil, Note and Sharpener is 7, 12 and 9 respectively.
Among the students that originally had Pencil, the numbers of students now having Eraser and scale is 3 and 9 respectively.
Among the students that originally had Eraser, the number of students now having Pen, Note and Sharpener is 4, 9, and 11 respectively.
Among the students that originally had Scale, the number of students now having Pen, Pencil, Eraser is 8, 7 and 9 respectively.
Among the students that originally had Note, the number of students now having Pen, Pencil and Sharpener is 7, 6and 20 respectively.
Among the students that originally had Sharpener, the number of students now having Eraser and Note is 18 and 16 respectively.
1) Among the students that originally had Pen, at least how many students must now have Scale?
a) 5
b) 3
c) 2
d) 1
e) 6
2) If out of the students that originally had Pen, the number of students now having Scale is 8, then find out of the students that now have Eraser?
a) 3
b) 2
c) 4
d) 1
e) 5
3) If among the students that originally had Note, the number of students now having Eraser is 1 more than the number of students now having Scale, then find the difference between the number of the students that now have Sharpener and Scale
a) 4
b) 3
c) 5
d) 6
e) 12
4) If among the students that originally had Sharpener, the number of students now having Eraser is twice the number of students now having Pen, then find out among the students that now having Scale which is one student more than the number of students that now having Pen?
a) 10
b) 9
c) 16
d) 15
e) 18
5) If among the students that originally had Pencil, the number of students now having Note is same as the number of students now having Scale, then find among the students that originally had Sharpener, the number of students now having pen
a) 7
b) 9
c) 8
d) 6
e) 10
Directions (6 – 10): Study the following information carefully and answer the given questions
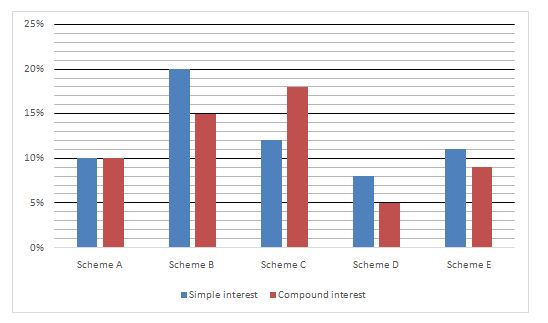
Given graph shows the percentage of interest in various schemes
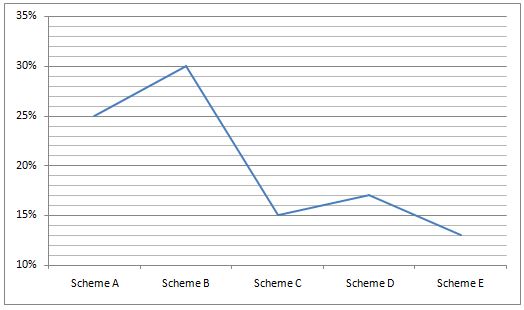
In graph percentage of total amount invested by Lalita in different schemes
There was four generations in a family tree Sohan, Sohan father, grandfather, great grandfather. The great grandfather whose age was 85 years in 1862 has 50000 of property with him whom he sold to a zamindar and invested it in the scheme A at simple interest. He died in 1870. After his death, Sohan grandfather received total amount. He invested it in scheme B in the year 1991 at compound interest and died after 2 years on the date of investment. After that Sohan father received Rs. 25 less than the total amount and he invested the amount partly in scheme A at compound interest and partly in the scheme D at simple interest. The ratio of investment done by Sohan father in scheme A to scheme D is 3:4
6) Find the amount received by Sohan if his father dies after three years of investment?
a) Rs.135870
b) Rs.148710
c) Rs.152201
d) Rs.135403
e) None of these
7) Lalita invested Rs.80000 according to the investment plan. What will be the difference in interest earned if she invests all her money in simple interest for 4 years and compound interest for 2 years following the investment plan?
a) Rs.97104
b) Rs.31480
c) Rs.21379
d) Rs.21889
e) Rs.17699
8) Lalita invested all her money in scheme B at compound interest for 3 years while her sister Babita invested all her money in scheme D at compound interest for 4 years. Total amount received by Lalita is approximately what percent to the total amount received by Babita, if the ratio of amount invested by Lalita to Babita is 5: 3?
a) 209%
b) 220%
c) 231%
d) 198%
e) 239%
9) Find the relation between the following two quantities:
Quantity I: Difference between the interests earned by Lalita on investing in scheme B at simple interest for 3 years and in scheme C at compound interest for 2 years investing Rs. X
Quantity II: Sum of interest earned by Lalita on investing in scheme A and scheme C at simple for 2 years investing Rs. X
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I = Quantity II (or) Relationship cannot be determined
d) Quantity I ≤ Quantity II
e) Quantity I ≥ Quantity II
10) Quantity I: Highest interest earned by Lalita investing at simple interest for 4 years investing Rs.10000
Quantity II: Amount received by Lalita investing in scheme C at compound interest for 2 years investing Rs.10000
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I = Quantity II (or) Relationship cannot be determined
d) Quantity I ≤ Quantity II
e) Quantity I ≥ Quantity II
Answers:
Directions (1 – 5):
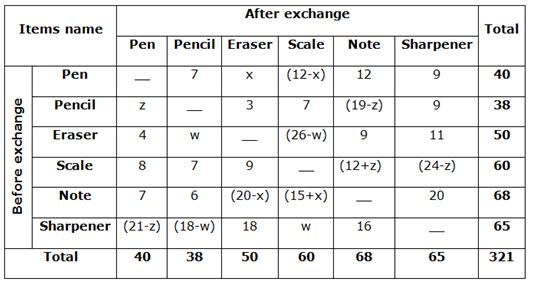
1) Answer: d)
From the above table, out of the students that originally had Pen, the number of students now having Scale is ‘12 – x’. Maximum possible value of x is 11.
Therefore minimum possible value of 12 – x
= 12 – 11= 1
2) Answer: c)
From the above table, out of the students that originally had Pen, the number of students now having Scale is 8 = (12-x)
8 = 12 –x
= > x = 4
Out of the students that originally had Pen, the number of students now having Eraser is 4.
3) Answer: b)
Among the students that originally had Note, the number of students now having Scale is a
Among the students that originally had Note, the number of students now having Eraser is b
From the above table, among the students that originally had Note, the total number of students now having Eraser and Scale is
(68 – 35) = 33 = (a + b) — (1)
= > (b – a) = 1 —- (2)
Solve the above equation (1) and (2), we get
= > a = 34/2 = 17
= > b = 16
Required difference = 20 – 17 = 3
4) Answer: a)
Among the students that originally had Sharpener, the number of students now having Eraser is 18
Among the students that originally had Sharpener, the number of students now having Pen be (18/2) = 9
Among the students that originally had Sharpener, the number of students now having Scale = 9 + 1 = 10
5) Answer: b)
From the above table,
Among the students that originally had Pencil, the number of students now having Note = among the students that originally had Pencil, the number of students now having Scale = 7
Among the students that originally had Pencil, the number of students now having Pen = 38 – (3+7+9+7) = 38 – 26 = 12 = z
Among the students that originally had Sharpener, the number of students now having pen = (21 – z)
= 21 – 12 = 9
Directions (6 – 10):
6) Answer: c)
For Great Grand Father
Principal Amount=Rs.50,000
Simple interest = p*r*t/100
=50000*10*8/100
=Rs.40,000
Amount= Principal + Simple Interest
=50000 + 40000 => Rs 90,000
For Grand Father
Principal amount = Rs.90000
Scheme B compound interest =15%
Time=2 years
Amount on compound interest = p*(1+r/100)t
=90000*(1+15/100)2
=>119025
For Sohan Father
Amount received by Sohan Father = 119025 – 25 = 119000
Amount invested in scheme A at compound interest for 3 years=119000*3/7
=>Rs.51000
Amount on compound interest =p*(1+r/100)t
=51000*(1+10/100)3
=>Rs.67881
Amount invested in scheme D at simple interest for 3 years=119000*4/7
=>Rs.68000
Amount on simple interest= P+ (P*r*t/100)
= 68000 + (68000*8*3/100) = 68000 + 16320
=>Rs.84320
Amount Sohan Received = 67881+ 84320=>Rs.152201
7) Answer: d)
For Scheme A:
Amount invested=25% of 80000= Rs.20000
Interest earned through simple interest = p*r*t/100
=20000*10*4/100 = Rs.8000
Interest earned through compound interest = = p*(1+r/100)t – P
= 20000*(1+10/100)2 – 20000
Interest earned=24200 – 20000 = 4200
Difference of interest= 8000 – 4200 = Rs.3800
For Scheme B:
Amount invested = 30% of 80000 = Rs.24000
Interest earned through simple interest = p*r*t/100
= 24000*4*20/100 = Rs.19200
Interest earned through Compound Interest= p*(1+r/100)t – p
= 24000*(1+15/100)2 – 24000
= Rs.31740 – 24000 = Rs.7740
Difference of interest = 19200 – 7740 = Rs.11460
For Scheme C:
Amount invested = 15% of 80000 =Rs.12000
Interest earned through simple interest=p*r*t/100
=12000*12*4/100 = Rs. 5760
Interest earned through Compound Interest= p*(1+r/100)t – p
=12000*(1 + 18/100)2 – 12000
=12000*59/50*59/50 – 12000
=16709 – 12000 = Rs.4709
Difference of interest= 5760 – 4709 = Rs.1051
For Scheme D:
Amount invested = 17% of 80000
Amount invested = Rs.13600
Interest earned through simple interest=p*r*t/100
=13600*8*4/100 =Rs.4352
Interest earned through Compound Interest= p*(1+r/100)t – p
= 13600*(1+5/100)2 – 13600
= 13600*105/100*105/100 – 13600
= 14994 – 13600 = Rs.1394
Difference of interest= 4352 – 1394= Rs.2958
For Scheme E:
Amount invested = 13% of 80000 = 10400
Interest earned through simple interest=p*r*t/100
=10400*11*4/100
=Rs.4576
Interest earned through Compound Interest= p*(1+r/100)t – p
=10400* (1+ 9/100)2 – 10400
= 10400*109/100*109/100 – 10400
=12356 – 10400 = 1956
Difference of interest = 4576 – 1956 = > Rs.2620
Total difference = 2620 + 2958 + 1051 + 3800 + 11460
= Rs.21889
8) Answer: a)
Let the amount invested by Lalita is 5X
Let the amount invested by Babita is 3X
Amount received by Lalita = p*(1+r/100)t
=5X*(1 +15/100)3
=5X*115/100*115/100*115/100 = 7.60 X
Amount received by Babita =p*(1+r/100)t
=3X*(1 +5/100)4
=3X*105/100*105/100*105/100*105/100
=3.64X
Required percentage= 7.60X/3.64X * 100
= 208.79% = 209%
9) Answer: b)
Quantity I:
For Scheme B
Amount invested = X*30% = Rs.0.3X
Interest earned through simple interest=p*r*t/100
0.3X*20*3/100 = 0.18X
For Scheme C
Amount invested= x*15% = 0.15X
Interest earned through compound interest= p*(1+r/100)t – p
= 0.15X*(1+18/100)2 – 0.15X
= 0.208X – 0.15X = 0.058X
Difference = 0.18X – 0.058X = 0.122X
Quantity II:
For Scheme A
Amount invested=X*25% = Rs.0.25X
Interest earned through simple interest=p*r*t/100
=0.25X*10*2/100 = 0.05X
For Scheme C
Amount invested=X*15% = Rs.0.15X
Interest earned through simple interest=p*r*t/100
=0.15X*12*2/100 = 0.036X
Total interest = 0.05X+0.036X
=>0.086X
Quantity I < Quantity II
10) Answer: a)
Quantity I: Amount invested=10000
For scheme A
Amount invested=10000*25% = Rs.2500
Interest earned through simple interest=p*r*t/100
=2500*10*4/100 = 1000
For Scheme B
Amount invested=10000*30% = Rs.3000
Interest earned through simple interest=p*r*t/100
=3000*20*4/100 = 2400
For Scheme C
Amount invested=10000*15% = Rs.1500
Interest earned through simple interest=p*r*t/100
=1500*12*4/100 = 720
For Scheme D
Amount invested=10000*17% = Rs.1700
Interest earned through simple interest=p*r*t/100
=1700*8*4/100 = 544
For Scheme E
Amount invested=10000*13% = Rs.1300
Interest earned through simple interest=p*r*t/100
=1300*11*4/100 = 572
Highest interest is earned by scheme B
(Or)
Amount invested in scheme B is highest at the same time Rate of interest in scheme B is highest compare than other schemes.
Amount invested=10000*30% = Rs.3000
Interest earned through simple interest=p*r*t/100
=3000*20*4/100 = 2400
Quantity I = 2400
Quantity II:
Amount invested=10000*15% = Rs.1500
Interest earned through compound interest= p*(1+r/100)t
=1500*(1+18/100)2
=1500*118/100*118/100
=Rs.2088
Quantity II = 2088
Hence Quantity I > Quantity II





