Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for LIC Assistant Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for LIC Assistant Mains Mock Test 2019
[WpProQuiz 7499]Application sums
1) Respective ratio of the income of Mahesh, Pranav, Neeraj and Khushi is 6:4:5:3 and respective ratio of their savings is 4:3:5:2. Expenditure of Mahesh is (200/3) % of his income. Expenditure of Neeraj is what percent of his income?
a) (100/3)%
b) 50%
c) (200/3) %
d) 25%
e) None of these
2) Respective ratio of the ages of Ravi and Bimal before six years was 13:11. Respective ratio of the age of Bimal before four years and age of Bimal after four years will be 3:4. Respective ratio of the present ages of Bimal and Vikash is 7:6. Find the difference between the present ages of Ravi and Vikash.
a) 10 years
b) 8 years
c) 6 years
d) 12 years
e) None of these
3) A motor boat can cover 171 Km downstream and 121 Km upstream in 20 hours. Speed of the motor boat in still water is 1 Km/h less than four times the speed of the stream. Downstream distance travelled by the motor boat in 15 hours is approximately what percent of the upstream distance travelled by the motor boat in 10 hours? (Assume that Speed of the motorboat in still water is a whole number)
a) 199%
b) 219%
c) 179%
d) 259%
e) 239%
4) Train X starts from station A towards station B with the speed of 25 Km/h. At the same time train Y starts from station B towards station A with the speed of 35 Km/h. Distance between station A and station B is 2100 Km. Find the difference between time taken by train X to reach station B after meeting with train Y and time taken by train Y to reach station A after meeting with train X.
a) 20 hours
b) 24 hours
c) 28 hours
d) 30 hours
e) None of these
5) Radius of the base of right circular cone is half of the radius of the base of a right circular cylinder having volume 24948 cm3 and height 18 cm. Slant height of the cone is 12 cm. Find the difference between curved surface areas of the cylinder and the cone.
a) 1860 cm2
b) 1620 cm2
c) 1740 cm2
d) 1980 cm2
e) None of these
Directions (6 – 10): Study the following information carefully and answer the questions given below:
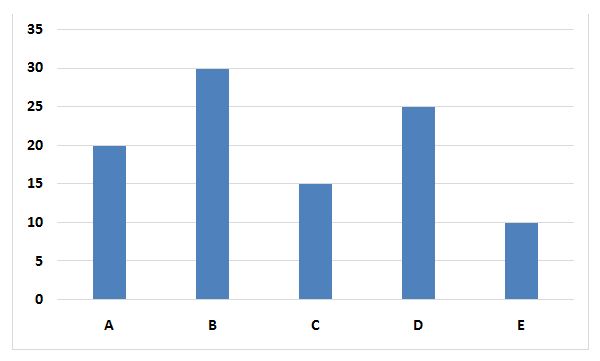
The following bar graph represents time (in minutes) taken by five pipes to fill an empty tank.
The following line graph represents time (in minutes) taken by five pipes to empty the filled tank.
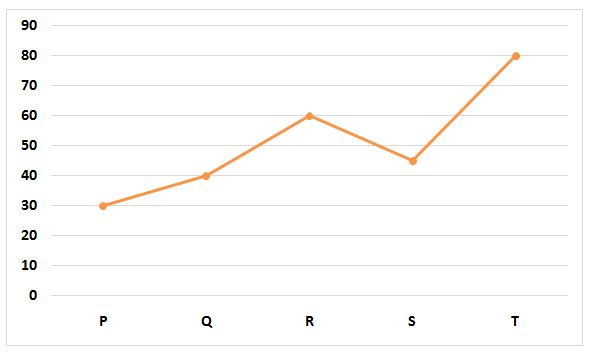
6) Pipe A, Pipe B and Pipe R are opened simultaneously and closed after 10 minutes. Find the time taken by pipe P to empty the filled part of the tank.
a) 30 minutes
b) 25 minutes
c) 20 minutes
d) 35 minutes
e) None of these
7) The tank was full. Pipe Q and Pipe R are opened for 20 minutes then closed. Find the time taken by Pipe C and Pipe E together to fill the remaining part of the tank.
a) 10 minutes
b) 5 minutes
c) 7 minutes
d) 8 minutes
e) None of these
8) Time taken by Pipe A and Pipe D to fill half of the tank is approximately what percent of the time taken by Pipe B and Pipe E to fill one fourth of the tank?
a) 100%
b) 150%
c) 250%
d) 200%
e) 300%
9) Find the respective ratio of the time taken by Pipe A, Pipe E and Pipe Q together to fill the tank and the time taken by Pipe B, Pipe D and Pipe S together to fill the tank.
a) 69:167
b) 83:115
c) 92:225
d) 79:213
e) None of these
10) If Pipe A work with half of its efficiency, Pipe B work with double of its efficiency and Pipe E works with 1/4th of its efficiency, find the time taken by them to fill the tank working together.
a) 70/11 minutes
b) 50/9 minutes
c) 40/3 minutes
d) 60/7 minutes
e) None of these
Answers:
Directions (1-5):
1) Answer: b)
Let, income of Mahesh, Pranav, Neeraj and Khushi be Rs.6x, Rs.4x, Rs.5x and Rs.3x respectively.
Now, Expenditure of Mahesh = ((200/3)/100) * 6x = 4x
Let, expenditure of Neeraj be Rs.k
According to the question
(6x – 4x) / (5x – k) = 4/5
=> 2x/(5x – k) = 4/5
=> 10x = 20x – 4k
=> 4k = 20x – 10x
=> k = 10x/4
=> k = 2.5x
Required percentage = 2.5x/5x * 100
= 50%
2) Answer: b)
Let, ages of Ravi and Bimal before six years be 13k and 11k respectively.
According to the question
(11k + 2)/(11k + 10) = 3/4
=> 44k + 8 = 33k + 30
=> 44k – 33k = 30 – 8
=> 11k = 22
=> k = 2
Present age of Ravi = 13k + 6 = 13 x 2 + 6 = 32 years
Present age of Bimal = 11k + 6 = 11 x 2 + 6 = 28 years
Present age of Vikash = 6/7 x 28 = 24 years
Required difference = 32 – 24 = 8 years
3) Answer: d)
Let, speed of the stream = y Km/h
Speed of the motor boat in still water = (4y – 1) Km/h
According to the question
[171/(4y – 1 + y)] + [121/(4y – 1 – y)] = 20=>[171/(5y – 1)] + [121/(3y – 1)] = 20
=> [171* (3y – 1) + 121 * (5y – 1)] / [(5y – 1) * (3y – 1) = 20
=> (513y – 171 + 605y – 121)/(15y2 – 8y + 1) = 20
=> 1118y – 292 = 300y2 – 160y + 20
=> 300y2 – 160y – 1118y + 20 + 292 = 0
=> 300y2 – 1278y + 312 = 0
=> 150y2 – 639y + 156 = 0
=>150y2 – 600y – 39y + 156 = 0
=> 150y(y – 4) – 39(y – 4) = 0
=> (y – 4)(150y – 39) = 0
=> y = 4, 39/150(rejected)
Speed of the stream = 4 km/h
Speed of the motor boat in still water = 4 * 4 – 1 = 15 Km/h
Required percentage = [(15 + 4) * 15]/[(15 – 4) * 10] * 100
= (19 * 15)/(11 *10) * 100
= 259.09%
= 259% approx.
4) Answer: b)
Total time taken by train X to reach station B = 2100/25 = 84 hours
Total time taken by train Y to reach station A = 2100/35 = 60 hours
Let, they meet after t hours from the time when they started their journey.
(25 + 35) * t = 2100
=> t = 2100/60
=> t = 35 hours
Required difference = (84 – 35) – (60 – 35)
= 49 – 25
= 24 hours
5) Answer: d)
We know that
Volume of a cylinder = πr2h
=> 24948 = 22/7 * r2 * 18
=> r2 = 24948 * 7/22 * 1/18
=> r2 = 441
=> r = 21 cm
We know that
Curved surface area of a cylinder = 2πrh
=> 2 * 22/7 * 21 * 18
= 2376 cm2
Radius of the cone = 21/2 = 10.5 cm
We know that
Curved surface area of a cone = πrl
= 22/7 * 10.5 * 12
= 396 cm2
Required difference = 2376 – 396 = 1980 cm2
Directions (6-10):
6) Answer: c)
Part of the tank filled = 10/20 + 10/30 – 10/60
= (30 + 20 – 10)/60
= 40/60
= 2/3
Let, required time taken = t minutes
t/30 = 2/3
=> t = 30 x 2/3
=> t = 20 minutes.
7) Answer: b)
Part of the tank emptied by Pipe Q and Pipe R in 20 minutes
= 20/40 + 20/60
= ½ + 1/3
= (3 + 2)/6
= 5/6
Let, required time taken = t minutes
t * (1/15 + 1/10) = 5/6
=> t * (2 + 3)/30 = 5/6
=> t = 30/5 * 5/6
=> t = 5 minutes
8) Answer: e)
Let, time taken by Pipe A and Pipe D to fill half of the tank = t minutes
And time taken by Pipe B and Pipe E to to fill one fourth of the tank = n minutes
t * (1/20 + 1/25) = ½
=> t * (5 + 4)/100 = ½
=> t = 100/9 * ½
=> t = 50/9 days
And
n * (1/30 + 1/10) = ¼
=> n * (1 + 3)/30 = ¼
=> n = 30/4 * ¼
=> n = 15/8 days
Required percentage = [(50/9)/(15/8)] x 100
= 296.2%
= 300% approx.
9) Answer: c)
Let, time taken by Pipe A, Pipe E and Pipe Q together to fill the tank = t minutes
And time taken by Pipe B, Pipe D and Pipe S together to fill the tank = n minutes
t * (1/20 + 1/10 – 1/40) = 1
=> t * (2 + 4 – 1)/40 = 1
=> t = 40/5
=> t = 8 minutes
And
n * (1/30 + 1/25 – 1/45) = 1
=> n *(15 + 18 – 10)/450 = 1
=> n = 450/23 minutes
Required ratio = 8 : 450/23 = 184 : 450 = 92:225
10) Answer: d)
Let, required time taken = t minutes
t * [1/(20 * 2) + 2/30 + 1/(10 * 4) = 1
=> t * (1/40 + 1/15 + 1/40) = 1
=> t * (3 + 8 + 3)/120 = 1
=> t = 120/14
=> t = 60/7 minutes





