Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7267]
Application sums
1) A machine produces articles at the rate of 50 units per hour. The articles sell for Rs. 100 each and the cost of production is Rs. 40 each. However, 20% of the articles have some defect and thus cannot be sold. The production rate of machine can be increased, but every increase of x units per hour would increase the production cost by 2x% and the number of defectives would become (20 + 1.5x)%. What is the maximum increase in production that can be undertaken without incurring losses?
a) 18 units
b) 16 units
c) 15 units
d) 17 units
e) None of these
2) I bought 3 apple and 5 banana at Rs. 67. After eating 1 apple, I sold the remaining fruits to Raja at Rs. 67. Raja, after eating 1 apple and 1 banana, sold the remaining fruits to Sam at Rs. 67. If Raja had an effective profit of 35% in this manner, how much percentage profit did I earn?
a) 40%
b) 27%
c) 20%
d) 41.25%
e) None of these
3) In 3 groups of children, there are 3 girls and 1 boy, 2 girls and 2 boys and 1 girl and 3 boys respectively. One child is selected at random from each group. What is the probability that 3 selected candidates are 1 girl and 2 boys?
a) 9/32
b) 13/32
c) 3/16
d) 1/16
e) None of these
4) On one day, Kajal is twice as likely to go to basketball, as she is likely to go for football practice. Given that Kajal necessarily goes for exactly one of the two activities each day, what is the probability that she goes to the basketball on 5 days out of 7 consecutive days of a specified week?
a) 28/729
b) 4/2187
c) 224/729
d) 16/2187
e) None of these
5) Find the sum of all the numbers that can be formed by using all the digits 6, 7, 8, 0 and are divisible by 12?
a) 50260
b) 43842
c) 60540
d) 48046
e) None of these
Data interpretation
Direction (6 – 10): Study the following data carefully and answer the questions:
There are five persons A, B, C, D and E that travelled their total journey by five different vehicles Car, Train, Bus, Bicycle and Foot. Table given below shows the speed (Km/h) of different vehicles for different persons.
Note: Dashes (—-) in the table shows that the person didn’t travel by that vehicle in his journey.
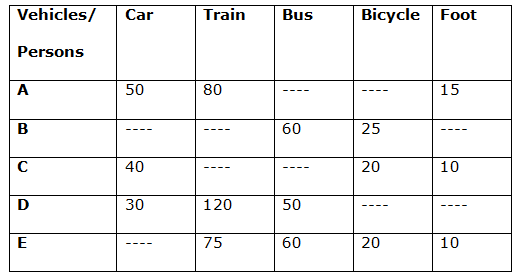
6) Person A travels same distance by car and by train and total time taken by him while travelling in Foot is 20 minutes. If distance travelled by Car is 8 times of that on Foot for person A, then what is the total time taken by person A to cover his journey?
a) 2 hours 22 minutes
b) 1 hour 12 minutes
c) 1 hour 38 minutes
d) 2 hour 2 minutes
e) None of these
7) If time taken by person B while travelling by Bus is 21 minutes more than the time taken by him while travelling by Bicycle and ratio of distance travelled by him by Bus to that by bicycle is 9: 2, then what is the total length of journey for person B?
a) 55 km
b) 75 km
c) 45 km
d) 60 km
e) None of these
8) If ratio of distance travelled by person C by Car, by Bicycle and on Foot is 6: 5: 1 respectively and total time taken by him in his journey is 2.5 hours, then how much less time he will take if he cover his complete journey by Car only?
a) 1.5 hour
b) 0.75 hour
c) 1.25 hour
d) 1 hour
e) None of these
9) Person D takes 40 minutes while travelling by Car and 22.5 minutes while travelling by Train. If he covers total 90 km in his journey, then what is the total time taken by person D while travelling by Bus?
a) 45 minutes
b) 30 minutes
c) 40 minutes
d) 20 minutes
e) None of these
10) If distance travelled by person E by Train and Bus is 30% and 20% respectively of the total distance of journey and distance travelled by Bicycle is 30 km more than that travelled on Foot. If total time taken by person E to cover his journey is 3 hours 44 minutes, then what is the total length of journey for person E?
a) 100 km
b) 80 km
c) 120 km
d) 90 km
e) None of these
Answers :
Directions (1-5) :
1) Answer: D
Revenue in 1 hour that will be generated = 100(50 + x) × (100 – 20 –1.5x)/100
The cost will be = 40(50 + x) × (100 + 2x)/100
Then Profit in the whole process = 2000 – 2.3x2 – 75x
So, if profit > 0, then x < 17.38
=>Hence maximum increase in production that can be taken without loss = 17.
2) Answer: C
Raja’s profit = (1 apple and 1 banana) on (2 apple and 5 banana) = 35%
=>apple + banana = 35/100(2 apple + 5 banana)
=> solving we get = 6 apple = 15 banana
=> apple/banana = 5/2
So, my effective profit = 1 apple on (3 apple and 5 banana)
= 1 apple / 3 apple + 5(2/5) apple
= 1 apple / 5 apple × 100 = 20%
Hence, my effective profit for the whole transaction is = 20%.
3) Answer: B
Getting one girl and two boys can be possible in three disjoint cases:
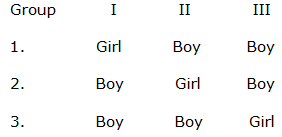
So P(I) = 3/4 × 2/4 × 3/4 = 9/32
P(II) = 1/4 × 2/4 × 3/4 = 3/32
P(III) = 1/4 × 2/4 × 1/4 = 1/32
So, the required probability = P(I) + P(II) + P(III)
=>9/32 + 3/32 + 1/32 = 13/32.
4) Answer: C
5 out of 7 days can be selected in 7c5 ways. In those 5 days, Kajal has to go to Basketball.
Probability = (2/3)5
On the other 2 days she has to go for football practice.
Probability = (1/3)2
Therefore required probability
= 7c5 × (2/3)5 × (1/3)2
= 224/729.
5) Answer: C
12 = (3 × 4).The number formed by all these digits will always be divisible by 3, because (6 + 7 + 8 + 0) = 21.
For divisibility by 4, last two digits should be 60 or 80 or 08 or 68 or 76.
If the last two digits are fixed we must make sure that the first digit is non-zero.
Case I: Last two digits are 60 or 80 or 08.
The first two digits can be arranged in 2 × 1 = 2 ways.
Case II: Last two digits are 68 or 76.
The first two digits can be arranged in 1 way, because the first digit cannot be 0.
So, sum = [(78 + 87) × 100 + 2 × 60] + [(67 + 76) × 100 + 2 × 80] + [(67 + 76) × 100 + 2 × 08] + 7068 + 8076 = 60540.
Directions (6-10) :
6) Answer: c)
Let distance travelled on Foot by person A = D
According to the question:
D/15 = (20/60)
D = 5 km
Distance travelled by Car and by Train by person A = 8 * 5 = 40 km
Time taken by person A to cover his journey by Car = 40/50 = 0.8 hours
Time taken by person A to cover his journey by Train = 40/80 = 0.5 hours
Required time = 0.8 + 0.5 + (20/60) = 1 hour 38 minutes
7) Answer: a)
Let distance travelled by person B by Bus and Bicycle is ‘9x’ and ‘2x’ respectively.
According to the question:
(9x/60) – (2x/25) = (21/60)
(0.15x) – (0.08x) = 0.35
0.07x = 0.35
x = 5
Required distance = 9x + 2x = 11x = 55 km
8) Answer: d)
Let distance travelled by person C by car, by Bicycle and on Foot is ‘6x’, ‘5x’ and ‘x’ respectively.
According to the question:
(6x/40) + (5x/20) + (x/10) = 2.5
0.15x + 0.25x + 0.1x = 2.5
0.5x = 2.5
x = 5
Total length of journey = 6x + 5x + x = 12x = 60 km
Total time taken by Car only = 60/40 = 1.5 hours
Required less time = 2.5 – 1.5 = 1 hour
9) Answer: b)
Distance travelled by person D while travelling by Car = 30 * (40/60) = 20 km
Distance travelled by person D while travelling by Train = 120 * (22.5/60) = 45 km
Total distance of his journey = 90 km
Distance travelled by person D while travelling by Bus = 90 – 20 – 45 = 25 km
Time taken by person D while travelling by Bus = 25/50 = 0.5 hours = 30 minutes
10) Answer: a)
Let total length of journey for person E = 100x
Distance covered by Train = 30% of 100x = 30x
Distance covered by Bus = 20% of 100x = 20x
Let distance covered by Bicycle and on Foot is ‘y + 30’ and ‘y’ respectively.
According to the question:
(y + 30) + y = 100x – 50x = 50x
2y = (50x – 30)
y = (25x – 15)
Now,
[30x/75] + [20x/60] + [(25x – 15 + 30)/20] + [(25x – 15)/10] = 3 + (44/60)0.4x + (x/3) + 1.25x + 0.75 + 2.5x – 1.5 = 3 + (11/15)
4.15x + (x/3) = 3.75 + (11/15)
(62.25x + 5x)/15 = (56.25 + 11)/15
67.25x = 67.25
x = 1
Total length of journey for person E = 100x = 100 km





