Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7327]
Data interpretation
Direction (1 – 5): Study the following data carefully and answer the questions:
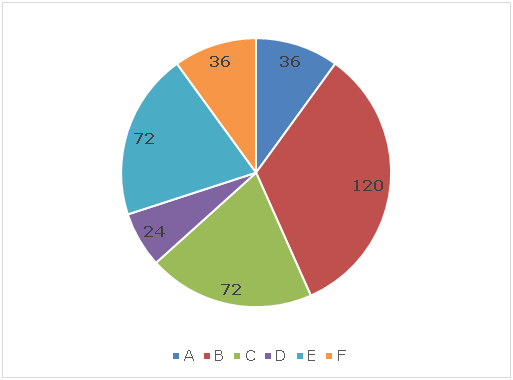
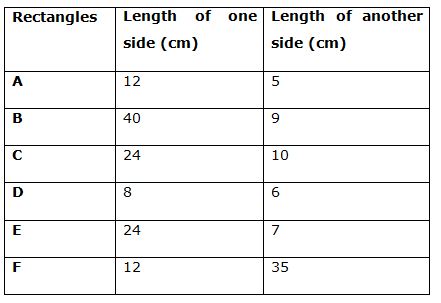
There are total 6 rectangles A, B, C, D, E and F, pie chart given below shows the distribution (degree) of length (cm) of one side of those 6 different rectangles.
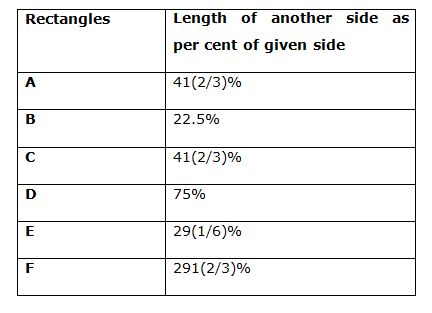
Table given below shows the length of another side of those 6 rectangles as a per cent of length of given side in the pie chart.
Sum of the pie chart = 120 cm
 1) Inside the rectangular filed C a cylindrical pit of radius 7 cm and depth 8.6 cm is dig. The soil coming out after digging is spread out over remaining part of the field, then what is the increment in the level of that rectangular field?
1) Inside the rectangular filed C a cylindrical pit of radius 7 cm and depth 8.6 cm is dig. The soil coming out after digging is spread out over remaining part of the field, then what is the increment in the level of that rectangular field?
a) 8.6 cm
b) 15.4 cm
c) 10.4 cm
d) 12.8 cm
e) None of these
2) If the cost of flooring is Rs.15/cm2 and cost of fencing is Rs.25/cm, then what is the ratio of cost of flooring the rectangular field A to the cost of fencing the rectangular field D?
a) 9: 7
b) 7: 5
c) 11: 9
d) 4: 3
e) None of these
3) There is an empty rectangular pool B of water and a tap is opened to fill the water into the pool. If the tap can fill the water up to a height of 5 cm in 12 minutes, then at what rate (litre/hour) the tap is filling the water in the pool?
a) 10
b) 12
c) 9
d) 6
e) None of these
4) A rectangular pool F is filled with water up to a height of 22 cm. If the pool is emptied by using a cylindrical bucket of base radius 3.5 cm and depth 12 cm, then how many such buckets are needed to be emptied the pool completely?
a) 10
b) 25
c) 30
d) 20
e) None of these
5) If the pools A and C are filled up to a height of 3 cm and 2.75 cm respectively and pool D is initially empty, whole volume of water from the pool A and C are poured into pool D. Similarly, pools E and B are filled up to a height of 5 cm and 12.25 cm respectively and pool F is initially empty and water from pools E and B are poured into pool F, then what is the ratio of height of water in pool D to that in pool F?
a) 7: 5
b) 9: 7
c) 5: 3
d) 11: 8
e) None of these
Data Interpretation
Direction (6 – 10): Study the following data carefully and answer the questions:
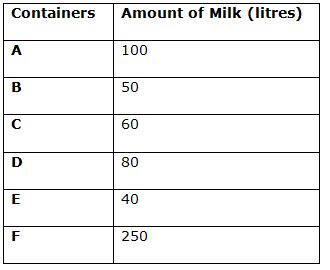
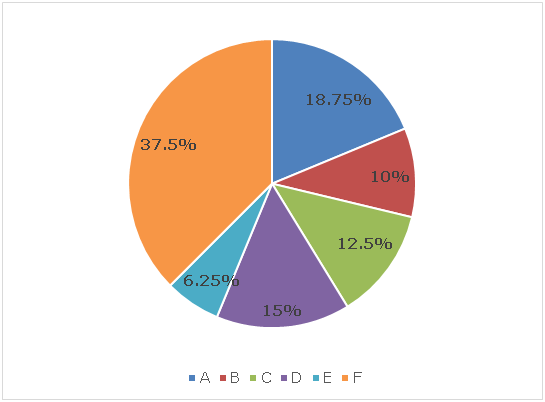
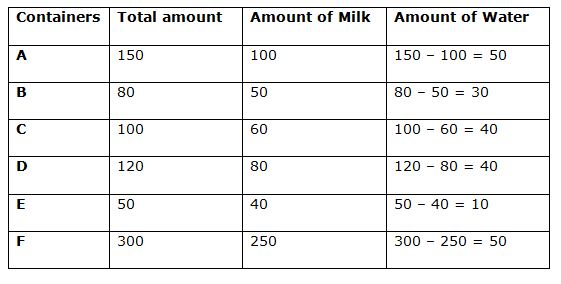
There are total six mixtures A, B, C, D, E and F of milk and water. Table given below shows the amount of milk in litres in those six mixtures. Pie chart given below shows the per cent distribution of total amount of those six mixtures respectively.
Sum of the pie chart = 800 litres
6) Mixtures from containers A and B are mixed in the ratio 3: 8 and he sold the mixture at the cost 23% less than the cost of pure milk, then what is the profit per cent earned after selling that mixture?
a) 21%
b) 16%
c) 27%
d) 18%
e) None of these
7) If the mixtures A and B are mixed in the ratio 3: 4 to form mixture P and mixture B and C are mixed in the ratio 8: 5 to form mixture Q. In what ratio mixture P and Q should be mixed to form a final mixture in which ratio of milk to water becomes 5: 3?
a) 7: 13
b) 5: 8
c) 9: 11
d) 4: 9
e) None of these
8) If 10 litres of the mixture E is taken out and replace with the same amount of water and this process is repeated one more time. Now, this final mixture is sold at the cost of Rs.10 per litre and cost price of pure milk is Rs.50 per litre, then what is the profit amount earned after selling this mixture?
a) Rs.180
b) Rs.260
c) Rs.220
d) Rs.160
e) None of these
9) Mixture D is mixed with mixture F in the ratio 2: 1 and 27 litres of water is also added, and a new mixture P is formed, then what is the amount of milk in the mixture P if the ratio of milk to water in mixture P becomes 5: 4?
a) 75 litres
b) 72 litres
c) 70 litres
d) 65 litres
e) None of these
10) ‘20’ litres of mixture from each container C and E are taken out and replaced with same amount of water. Now, mixtures from these two containers are poured into a large container, then what is the ratio of milk to water in large container?
a) 11: 12
b) 10: 11
c) 13: 14
d) 9: 10
e) None of these
Answers :
Directions (1 – 5):
Length of one side of rectangle A = 120 * (36/360) = 12 cm
Length of another side of rectangle A = 41(2/3)% of 12 = 5 cm
Length of one side of rectangle B = 120 * (120/360) = 40 cm
Length of another side of rectangle B = 22.5% of 40 = 9 cm
Length of one side of rectangle C = 120 * (72/360) = 24 cm
Length of another side of rectangle C = 41(2/3)% of 24 = 10 cm
Length of one side of rectangle D = 120 * (24/360) = 8 cm
Length of another side of rectangle D = 75% of 8 = 6 cm
Length of one side of rectangle E = 120 * (72/360) = 24 cm
Length of another side of rectangle E = 29(1/6)% of 24 = 7 cm
Length of one side of rectangle F = 120 * (36/360) = 12 cm
Length of another side of rectangle F = 291(2/3)% of 12 = 35 cm
1) Answer: b)
Area of field C = 24 * 10 = 240 cm2
Base area of cylindrical pit = (22/7) * 72 = 154 cm2
Remaining area of the filed = 240 – 154 = 86 cm2
Volume of the soil coming out after digging the pit = (22/7) * 72 * 8.6 = 1324.4 cm3
Increment in the level of the filed = 1324.4/86 = 15.4 cm
2) Answer: a)
Area of field A = 12 * 5 = 60 cm2
Cost of flooring the rectangular field A = 15 * 60 = Rs.900
Perimeter of field D = 2 * (8 + 6) = 28 cm
Cost of fencing the rectangular field D = 28 * 25 = Rs.700
Required ratio = 900: 700 = 9: 7
3) Answer: c)
Base area of pool B = 40 * 9 = 360 cm2
Volume of the water in tank after 12 minutes = 360 * 5 = 1800 cm3 = 1.8 litres
Let the rate at which tap is filling the pool = ‘x’ litres/hour
According the question:
x * (12/60) = 1.8
x = (1.8 * 60)/12
x = 9 litres/hour
4) Answer: d)
Total volume of water in the pool F when it is filled up to height of 22 cm = (12 * 35 * 22) cm3
Volume of 1 such bucket = (22/7) * 3.52 * 12 = (22 * 21) cm3
Let number of such buckets needed = ‘N’
According to the question:
(22 * 21) * N = (12 * 35 * 22)
N = (12 * 35 * 22)/(22 * 21)
N = 20
5) Answer: a)
Let the height of water in pool D and F is ‘x’ and ‘y’ respectively.
Total volume of water in pool D = Total volume of water in pools A and C
= (12 * 5 * 3) + (24 * 10 * 2.75)
(8 * 6 * x) = 180 + 660
48x = 840
x = 17.5 cm
Total volume of water in pool F = Total volume of water in pools E and B = (24 * 7 * 5) + (40 * 9 * 12.25)
(12 * 35 * y) = 840 + 4410
420y = 5250
y = 12.5 cm
Required ratio = x: y = 17.5: 12.5 = 7: 5
Directions (6 – 10):
Total amount of mixture A = 18.75% of 800 = 150 litres
Total amount of mixture B = 10% of 800 = 80 litres
Total amount of mixture C = 12.5% of 800 = 100 litres
Total amount of mixture D = 15% of 800 = 120 litres
Total amount of mixture E = 6.25% of 800 = 50 litres
Total amount of mixture F = 37.5% of 800 = 300 litres
6) Answer: a)
Part of milk in container A = 100/150 = 2/3
Part of milk in container B = 50/80 = 5/8
Let the part of milk in the final mixture = X
By the rule of alligation:
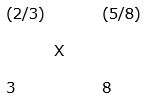
5 – 8X = 3X – 2
11X = 7
X = 7/11
Ratio of milk to water in final mixture = 7: (11 – 7) = 7: 4
Cost price of mixture = (7 * 1) + (4 * 0) = 7
Selling price of mixture = (7 + 4) * 77% of 1 = 8.47
Profit per cent = [(8.47 – 7)/7] * 100 = 21%
7) Answer: a)
Part of milk in mixture A = 100/150 = 2/3
Part of milk in mixture B = 50/80 = 5/8
Part of milk in mixture C = 60/100 = 3/5
By the rule of alligation:

2.5 – 4P = 3P – 2
4.5 = 7P
P = 45/70 = 9/14
By the rule of alligation:
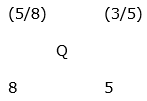
3 – 5Q = 8Q – 5
13Q = 8
Q = 8/13
By the rule of alligation:
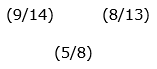
= [(1/104)]: [(1/56)]
= 56: 104
= 7: 13
8) Answer: c)
Amount of milk in mixture E when 20 litres of mixture E is replaced by same amount of water two times = 40 * [1 – (20/50)]2
= 40 * (3/5)2
= 14.4 litres
Amount of water = 50 – 14.4 = 35.6 litres
Cost price of mixture = 14.4 * 50 = Rs.720
Selling price of mixture = 50 * 10 = Rs.500
Profit amount = 720 – 500 = Rs.220
9) Answer: d)
Part of milk in mixture D = 80/120 = 2/3
Part of milk in mixture F = 250/300 = 5/6
By the rule of alligation:

(5/6) – P = 2P – (8/6)
3P = (13/6)
P = 13/18
Let amount of milk and water is 13a and (18a – 13a = 5a) respectively.
According to the question:
13a: (5a + 27) = 5: 4
52a = 25a + 135
27a = 135
a = 5
Amount of milk in mixture P = 13a = 65 litres
10) Answer: e)
Amount of milk in container C after replacement = 60 * [1 – (20/100)]
= 48 litres
Amount of water in container C after replacement = 100 – 48 = 52 litres
Amount of milk in container E after replacement = 40 * [1 – (20/50)] = 24 litres
Amount of water in container E after replacement = 50 – 24 = 26 litres
Required ratio = (48 + 24): (52 + 26) = 72: 78 = 12: 13





