Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7339]
Quantity based questions
Directions (1 – 5): Each question contains three quantities as Quantity I, quantity II and Quantity III. You have to determine the relationship between them and give answer as,
1)
Quantity I: Nithya can do a job in 15 days alone and Priya can do the same job in 18 days alone. A third person Kalai whose efficiency is (5/11)th of efficiency of both Nithya and Priya together, can do the same job in how many days alone?
Quantity II: A and B together can do a piece of work in 120/11 days. If A and B receives Rs.600 and Rs.500 respectively, then find the number of days taken by B alone.
Quantity III: P and Q together can do a piece of work in 20/3 days. R and S together can do the same work in 10 days. Q and R together can do the same work in 6 days. Find the number of days taken by P alone to complete the work, if S alone can do the same work in 30 days.
Which of the following should be placed in the blank spaces of the expression “Quantity I__ Quantity II___Quantity III” from left to right with respect to the above statements?
a) >, <
b) <, >
c) >, =
d) >, ≥
e) ≤, ≥
2)
Quantity I: Marked price of an article is 50% more than the cost price. If the shopkeeper gives discount of 10% and cost price of that article is Rs 100 and he sale his 40 articles, then find the profit earned by him.
Quantity II: Seeta bought an article at 10% discount on the marked price. Seeta marks 20% above and sells to Geeta at a discount of 20%. If Geeta pays Rs. 864, then find the marked price of an article.
Quantity III: A and B enter into a partnership with a capital ratio of 4: 5. After 3 months, A withdrew 3/4th and receives Rs.3500 from the total profit at the end of the year, then find the total profit.
Which of the following should be placed in the blank spaces of the expression “Quantity I__ Quantity II___Quantity III” from left to right with respect to the above statements?
a) >, <
b) =, <
c) >, =
d) >, ≥
e) ≤, ≥
3)
Quantity I: 6 hrs
Quantity II: A man can covers 48 km distance in 4 hours. If he increases his speed by 20% then find the time taken to cross 72 km.
Quantity III: Pipe A, B and C together can fill a tank in 8 hrs, while C and A together can fill a tank in 12 hrs. If A is 33(1/3)% efficient of pipe C, then find the time taken by Pipe B and C together to the fill the tank?
Which of the following should be placed in the blank spaces of the expression “Quantity I__ Quantity II___Quantity III” from left to right with respect to the above statements?
a) >, <
b) =, <
c) >, =
d) >, ≥
e) ≤, ≥
4)
Quantity I: There are 6 men and 6 women in a class, from these 4 members are to be selected to form a committee. Find the number of ways that at least two women were in the committee.
Quantity II: A and B together can do a piece of work in 6 (6/7) days with the help of C finishes in 5 (1/3) days. If C got Rs.200 as wage, then find the total wages of A, B and C.
Quantity III: A retailer purchases a sewing machine at discount of 15% and sells it for Rs.1955. In the bargain he makes a profit of 15%. How much is the discount which he got from the wholesale?
Which of the following should be placed in the blank spaces of the expression “Quantity I__ Quantity II___Quantity III” from left to right with respect to the above statements?
a) >, <
b) =, <
c) >, =
d) <, >
e) ≤, ≥
5)
Quantity I: In a class 45 students boys and girls are in the ratio of 5: 4. The average age of boys is 36 years and a girl is 22.5 years. Find the average age of the class
Quantity II: The ages of Rahul and Praveen are 40 years and 60 years, respectively. How many years before the ratio of their ages was 3: 5?
Quantity III: The ages of Sam and Sudha are in the ratio of 4: 5. After 12 years the ratio of their ages will be 7: 8. What is the difference in their ages?
Which of the following should be placed in the blank spaces of the expression “Quantity I__ Quantity II___Quantity III” from left to right with respect to the above statements?
a) >, <
b) =, <
c) >, >
d) >, ≥
e) ≤, ≥
Data Interpretation
Directions (6 – 10): Study the following information carefully and answer the given questions.
Three persons X, Y, Z have undertaken the five different works A, B, C, D, and E as they can complete the work alone shown in the graph.
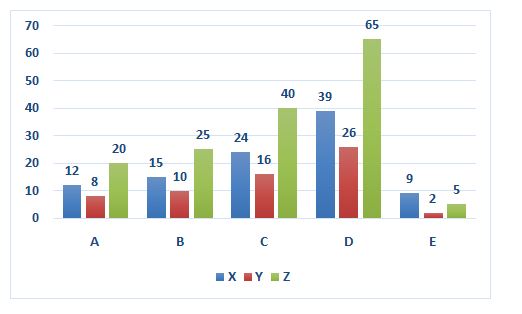
6) X and Y started the work A and work for two days and then Y left , after that X and Z take over the work and works alternatively, then in how many days the total work has completed?
a) 11 3/5 days
b) 09 2/5 days
c) 10 3/5 days
d) 11 2/5 days
e) 12 2/5 days
7) Work C is completed by X and Z in the ratio of 1:3 then what is the difference between the number of days taken by them if they worked alone while they completed their part of work C?
a) 16 days
b) 28 days
c) 10 days
d) 24 days
e) 25 days
8) How many days P alone can complete the work E?
Statement I: P takes twice the time to complete the work A.
Statement II: Q takes twice time as X to complete the wok E.
Statement III: If P and Q can complete the work E in 9 days.
A) If the data in statement I and II are sufficient to answer the question, while the data in statement III are not sufficient to answer the question.
B) If the data in statement I alone or in the statement II alone or in the statement III alone is sufficient to answer the question.
C) If the data in statement I and III are sufficient to answer the question, while the data in statement II is not sufficient to answer the question.
D) If the data in statement II and III are sufficient to answer the question, while the data in statement I is not sufficient to answer the question.
E) If the data in all the statement I, II and III are necessary to answer the question
9) If R alone completes the work A in 10 days and S alone can complete the work B is equal to the 1/4th of the time taken by Z to complete the work C. If R and S work alternatively then how many days they take to complete the work E if work started by R?
a) 5 (3/5) days
b) 8 (3/4) days
c) 6 (3/5) days
d) 5 (3/4) days
e) 10 (2/3) days
10) Quantity I: Z started the work E and left after five days. Then X is continuing that work and completed the reaming work.In how many days the total work has completed?
Quantity II: Y started the work B for 5 days and left then Z complete the remaining work. In how many days the total work has completed?
a) Quantity I < Quantity II
b) Quantity I > Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II or relationship cannot be established
Answers:
Directions (1-5):
1) Answer: b)
Quantity I:
According to the question,
One day work of Nithya and Priya together = (1/15) + (1/18)
= 11/90
Thus number of days taken by Kalai to complete the work = (90/11) * (11/5)
= 18 days
Quantity II:
Efficiency ratio of A and B = 600: 500 = 6: 5
Time ratio of A and B = 5: 6 = 5x : 6x
According to the question,
1/5x + 1/6x = 11/120
11/30x = 11/120
x = 4
Number of days taken by B alone = 6 * 4 = 24 days
Quantity III:
(P+ Q)’s one day work = 3/20
(Q+R)’s one day work = 1/6
(R+S)’s one day work = 1/10
R’s one day work = 1/10 – 1/30 = (3 – 1)/30 = 2/30 = 1/15
Q’s one day work = 1/6 – 1/15 = (5 – 2)/30 = 3/30 = 1/10
P’s one day work = 3/20 – 1/10 = (3 – 2)/20 = 1/20
P can complete the work in 20 days
2) Answer: a)
Quantity I:
Let CP = 100
Then MP = 150
Now SP = (90/100) * 150
= 135
Thus profit percentage = 35%
Hence required amount = 100 * 40 * 35/100
= Rs.1400
Quantity II:
Let us take marked price of an article be Rs. X
According to the question,
x * 90/100 * 120/100 * 80/100 = 864
x = 864 * 100/90 * 100/120 * 100/80
x = Rs. 1000
Quantity III:
Profit ratio of A and B = (4x * 3+ 4x * 1/4 * 9): (5x * 12)
= (12x + 9x): 60x
= 21x: 60x
= 7: 20
Let us take the total profit be x
A’s share in the total profit = 3500
x * (7/27) = 3500
=> x = 500 * 27 = Rs.13500
3) Answer: a)
Quantity I: 6 hrs
Quantity II:
Original speed = 48/4 = 12 km/hr
New speed = 12 * 120/100 = 14.4 km/hr
Required time = 72/14.4 = 5 hrs
Quantity III:
A + B + C = 8hrs
A + C = 12hrs
LCM of (8,12) = 24
Number of units of water filled by A, B and C together = 24/8 = 3 units
Number of units of water filled by A and C together = 24/12 = 2 units
(i.e.) Number of units of water filled by B = 3 – 2 = 1 units
Number of units of water filled by C in one hour = x units
Number of units of water filled by A in one hour = 33(1/3)% of x = x/3
A + C = 2 units
x + x/3 = 2
x = 1.5 units
Water filled by B and C together = 1 + 1.5 = 2.5 units
Time = 24/2.5 = 9.6 hrs
4) Answer: d)
Quantity I:
Number of ways = (6C2 * 6C2) + (6C3 * 6C1) + (6C4)
= [(6 *5 /1 * 2) * (6 * 5/1(1 * 2)]+ [(6 * 5 * 4/1 * 2 * 3) * 6] + (6 * 5/1 * 2)
= (15 * 15) + (20 * 6) + 15
= 225 + 120 + 15
= 360
Quantity II:
C’s one day work = 3/16 – 7/48
= (9 – 7)/48
= 2/48
= 1/24
(A + B)’s one day work: C’s one day work = 7/48: 1/24
= 7: 2
C’s share = 2/9 of total wage = 200
Total wage = (200/2) * 9 = Rs.900
Quantity III:
Let the marked price be Rs. x
Discount = 15% of Rs. x
C.P. = (x – 15% of x) = Rs. 17x / 20
Then 15% of 17x / 20 = 1955 – 17x / 20
51x/400 + 17x/20 = 1955
x = 2000
Discount received by retailer = (15% of 2000) = Rs.300.
5) Answer: c)
Quantity I:
According to the question,
45 * x = 25 * 36 + 20 * 22.5
45x = 900 + 450
x =1350/45 = 30 yrs
Quantity II:
Let x year ago, the ratio of Rahul and Praveen’s ages was 3: 5
(40 – x)/(60 – x) = 3/5
=> 200 – 5x = 180 – 3x
=> x = 10 years
Quantity III:
(4x + 12)/(5x + 12) = 7/8
32x + 96 = 35x + 84
3x = 12
x = 4
Difference in their ages = (5x – 4x) = x = 4 years
Directions (6-10):
6) Answer: c)
LCM of number of Days for work A done by X, Y, Z alone is 120, consider this is the total parts of work.
Efficiency of work per day for X, Y, Z is in the ratio of 10:15:6
For the first two days 50 parts of total work has completed
Remaining 70 parts are done by X and Z in alternative days. so every two days,16 parts completed
After (8 days) 4 full cycle, 4* 16=64 parts completed 6 parts remained
X again start the work and completed in 3/5 days
So the work completed in 10 3/5 days
7) Answer: d)
LCM of Days for work C is done by X, Y, Z alone is240, consider this is the total part of work.
Efficiency of work per day for X, Y, Z is in the ratio of 10:15:6
Work done by X and Z individually is 60 and 180 parts respectively
X completed its 60 parts in 60/10= 6 days
Z completed its 180 parts in180/6= 30 days
The difference between the number of days is 24.
8) Answer: d)
Statement I: we cannot compare work A and work E and solve it.
Statement II: From the chart, LCM of number Days for work E done by X, Y, Z alone is 90, and Efficiency is in the ratio of 10: 15: 6 for X: Y: Z Respectively and Q can complete the work in 18 days.
By combining, statement II and Statement III,
Total parts per day* Number of Days = Total Parts of Work
(5+P) 9= 90
P=5 parts per day
So P alone can complete the work in 18 days.
9) Answer: c)
LCM of number of Days for work A done by X, Y, Z and R alone is 120, consider this is the total part of work A
The Efficiency of R is 12 parts per day
S takes ¼th of total time by Z for work C= 10 days
LCM of Days for work B done by X, Y, Z and S alone is 150, consider this is the total part of work B
The Efficiency of S is 15 parts per day
LCM of Days for work E done by X, Y, Z alone is 90, consider this is the total part of work E
For every two days they completed 27 parts
After the 3 full cycles (6 days) they completed 27*3 = 81 parts, reaming 9 parts done by S in 3/5 of a Day
So the total work is completed in 6 3/5 days.
10) Answer: a)
Quantity I:
LCM of Days for work E done by X, Y, Z alone is 90, consider this is the total part of work E
Efficiency of work per day for X, Y, Z is in the ratio of 10: 15: 6
Total parts per day* Number of Days = Total Parts of Work
6*5 + 10 XD= 90
XD= 6
So total number of days is 11 days
Quantity II:
LCM of Days for work B done by X, Y, Z and S alone is 150, consider this is the total part of work B
Efficiency of work per day for X, Y, Z is in the ratio of 10:15:6
Total parts per day* Number of Days = Total Parts of Work
15*5 + 6 * ZD= 150
ZD = 12.5, So total number of days is 17.5 days





