Dear Readers, Bank Exam Race for the Year 2019 is already started, To enrich your preparation here we have providing new series of Practice Questions on Quantitative Aptitude – Section. Candidates those who are preparing for NIACL AO Mains 2019 Exams can practice these questions daily and make your preparation effective.
[WpProQuiz 5103]
Click here to take NIACL AO Mock Test
Directions (Q. 1 – 5): In the following questions, two equations I and II are given. You have to solve both the equations and give answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established
1) I) x = [√(24782 – 1678)] × ∜2401 ÷ (52 + 3)
II) y = ∛74088
2) I) 3x2 + 33x + 72 = 0
II) 2y2 – y – 55 = 0
3) I) 2x2 + (52 – 57) x – (132 ÷ 4) = 0
II) 7y2 – 16y – 15 = 0
4) I) 7x – 6y = -21
II) 2x – 3y = 15
5) I) x2 – 8x – 65 = 0
II) y2 – y – 42 = 0
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following bar graph shows the total number of items (In lakhs) produced by two different companies in 6 different years.
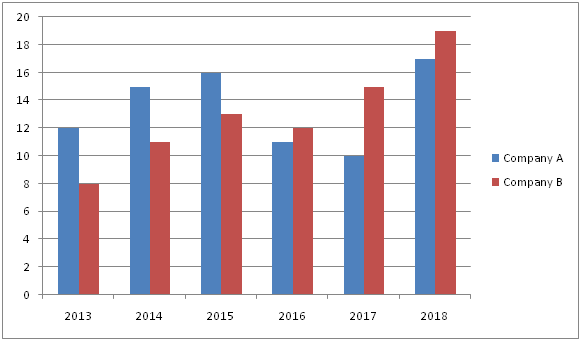
6) Find the ratio between the total number of items sold by the company A in the year 2013 and 2015 together to that of total number of items produced by company B in the year 2014 and 2016 together, if the ratio between the total number of sold to that of unsold items of company A in the year 2013 is 7 : 5 and the percentage of unsold items of company A in the year 2015 is 28 %?
a) 152: 257
b) 265: 389
c) 463: 575
d) 314: 437
e) None of these
7) Find the difference between the average number of items produced by company A to that of company B in all the given years together?
a) 50000
b) 40000
c) 75000
d) 60000
e) None of these
8) Find the sum of the number of items sold by company A in the year 2015 and the number of items remains unsold by company B in the year 2017 together, if the percentage of items sold by company A in the year 2015 is 60 % and the percentage of items sold by company B in the year 2017 is 62 %?
a) 13.6 lakhs
b) 12.8 lakhs
c) 16.4 lakhs
d) 15.3 lakhs
e) None of these
9) Total number of items produced by company A and B together in the year 2013 and 2016 together is approximately what percentage of total number of items produced by company A and B together in the year 2014 and 2018 together?
a) 62 %
b) 70 %
c) 94 %
d) 106 %
e) 85 %
10) If in the year 2018 of company A, the 4 % of items were damaged and then the ratio between the total number of items sold to that of unsold is 5: 3, then find the average number of items sold by company A in the year 2018 and the number of items produced by company B in the year 2017 together?
a) 1960000
b) 2340000
c) 2520000
d) 1850000
e) None of these
Answers :
Direction (1-5 ) :
1) Answer: c)
I) x = [√(24782 – 1678)] × ∜2401 ÷ (52 + 3)
X = √23104 × ∜2401 ÷ 28
X = (152*7)/28 = 38
II) y = ∛74088 = 42
X < y
2) Answer: e)
I) 3x2 + 33x + 72 = 0
3x2 + 24x + 9x + 72 = 0
3x (x + 8) + 9 (x + 8) = 0
(3x + 9) (x + 8) = 0
X = -9/3, -8 = -3, -8
II) 2y2 – y – 55 = 0
2y2 + 10y – 11y – 55 = 0
2y (y + 5) – 11 (y + 5) = 0
(2y – 11) (y + 5) = 0
Y = 11/2, -5 = 5.5, -5
Can’t be determined
3) Answer: e)
I) 2x2 + (52 – 57) x – (132 ÷ 4) = 0
2x2 – 5x – 33 = 0
2x2 + 6x – 11x – 33 = 0
2x (x + 3) -11 (x + 3) = 0
(2x – 11) (x + 3) = 0
X = 11/2, -3 = 5.5, -3
II) 7y2 – 16y – 15 = 0
7y2 – 21y + 5y – 15 = 0
7y (y – 3) + 5 (y – 3) = 0
(7y + 5) (y – 3) = 0
Y = -5/7, 3 = -0.714, 3
Can’t be determined
4) Answer: c)
7x – 6y = -21 —> (1)
2x – 3y = 15 —> (2)
By solving the equation (1) and (2), we get,
X = 3, y = 7
X < y
5) Answer: e)
I) x2 – 8x – 65 = 0
(x – 13) (x + 5) = 0
X = 13, -5
II) y2 – y – 42 = 0
(y + 6) (y – 7) = 0
Y = -6, 7
Can’t be determined
Direction (6-10) :
6) Answer: c)
The total number of items sold by the company A in the year 2013 and 2015 together
= > 1200000*(7/12) + 1600000*(72/100)
= > 700000 + 1152000 = 1852000
The total number of items produced by company B in the year 2014 and 2016 together
= > 11 + 12 = 23 lakhs
Required ratio = 1852000: 2300000 = 463: 575
7) Answer: a)
The average number of items produced by company A in all the given years together
= > (12 + 15 + 16 + 11 + 10 + 17)/6 = 81/6
The average number of items produced by company B in all the given years together
= > (8 + 11 + 13 + 12 + 15 + 19)/6 = 78/6
Required difference = (81/6 – 78/6) = (3/6) lakhs = 50000
8) Answer: d)
The number of items sold by company A in the year 2015
= > 16*(60/100) = 9.6 lakhs
The number of items remains unsold by company B in the year 2017
= > 15*(38/100) = 5.7 lakhs
Required total = 9.6 + 5.7 = 15.3 lakhs
9) Answer: b)
Total number of items produced by company A and B together in the year 2013 and 2016 together
= > 12 + 8 + 11 + 12 = 43 lakhs
Total number of items produced by company A and B together in the year 2014 and 2018 together
= > 15 + 11 + 17 + 19 = 62 lakhs
Required % = (43/62)*100 = 70 %
10) Answer: c)
The total number of items sold by company A in the year 2018 and the number of items produced by company B in the year 2017 together
= > 1700000*(96/100)*(5/8) + 1500000
= > 1020000 + 1500000 = 2520000





