Dear Readers, Bank Exam Race for the Year 2019 is already started, To enrich your preparation here we have providing new series of Practice Questions on Quantitative Aptitude – Section. Candidates those who are preparing for NIACL AO Mains 2019 Exams can practice these questions daily and make your preparation effective.
[WpProQuiz 5149]
Click here to take NIACL AO Mock Test
Directions (Q. 1 – 5): In the following questions, two equations I and II are given. You have to solve both the equations and give answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established
1)
I) 2x2 + 21x + 49 = 0
II) 4y2 + 48y + 23 = 0
2)
I) 5x – 3y = -1
II) 3x – 2y = 0
3)
I) x2 – 24x – 81 = 0
II) y2 – 21y – 72 = 0
4)
I) x = (∛157464 ÷ 6) + (72 × 56) ÷ 64
II) y = ∜20736 + 82 + (512 ÷ 128)
5)
I) 3x2 + 25x + 52 = 0
II) 2y2 + 23y + 66 = 0
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions.
The following pie chart 1 shows the total number of students who appeared for IAS exam from 5 different states and the pie chart 2 shows the total number of successful candidates of IAS examination from 5 different states.
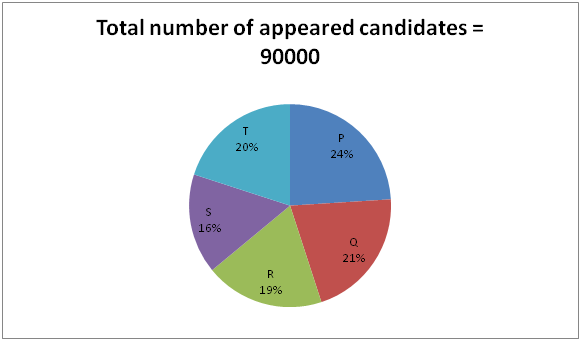
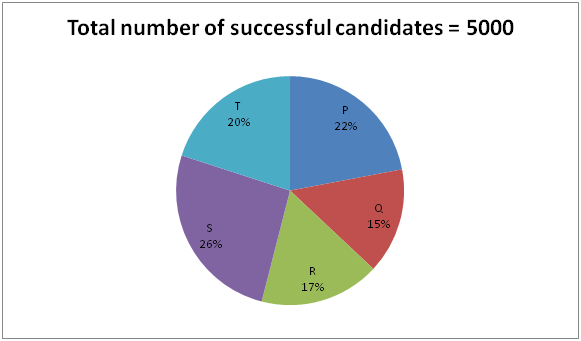
6) Total number of successful candidates of IAS examination from state S is approximately what percentage of total number of candidates appeared for IAS examination from state P?
a) 12 %
b) 25 %
c) 34 %
d) 6 %
e) 18 %
7) Find the ratio between the total number of candidates appeared for IAS examination from state Q and S together to that of total number of successful candidates of IAS examination from state P, Q, R and T together?
a) 9 : 1
b) 111: 23
c) 75: 28
d) 52: 13
e) None of these
8) Find the difference between the total number of unsuccessful candidates of State R to that of State S?
a) 2780
b) 3360
c) 3150
d) 3025
e) None of these
9) Find the average number of unsuccessful candidates of State P, Q and R together?
a) 17500
b) 18300
c) 17900
d) 18700
e) None of these
10) Total number of candidates appeared for IAS examination from state P and Q together is what percentage more/less than the total number of candidates appeared for IAS examination from S and T together?
a) 15 %
b) 20 %
c) 30 %
d) 25 %
e) None of these
Answers :
Direction (1-5 ) :
1) Answer: e)
I) 2x2 + 21x + 49 = 0
2x2 + 14x + 7x + 49 = 0
2x (x + 7) + 7(x + 7) = 0
(2x + 7) (x + 7) = 0
X = -7/2, -7 = -3.5, -7
II) 4y2 + 48y + 23 = 0
4y2 + 2y + 46y + 23 = 0
2y (2y + 1) + 23 (2y + 1) = 0
(2y + 23) (2y + 1) = 0
Y = -23/2, -1/2 = -11.5, -0.5
Can’t be determined
2) Answer: a)
5x – 3y = -1 —> (1)
3x – 2y = 0 —> (2)
By solving (1) and (2), we get,
X = -2, y = -3
X > y
3) Answer: e)
I) x2 – 24x – 81 = 0
(x – 27) (x + 3) = 0
X = 27, -3
II) y2 – 21y – 72 = 0
(y – 24) (y + 3) = 0
Y = 24, -3
Can’t be determined
4) Answer: c)
I) x = (∛157464 ÷ 6) + (72 × 56) ÷ 64
X = (54/6) + (72*56)/64
X = 9 + 63 = 72
II) y = ∜20736 + 82 + (512 ÷ 128)
Y = 12 + 64 + 4 = 80
X < y
5) Answer: a)
I) 3x2 + 25x + 52 = 0
3x2 + 12x + 13x + 52 = 0
3x (x + 4) + 13(x + 4) = 0
(3x + 13) (x + 4) = 0
X = -13/3, -4 = -4.33, -4
II) 2y2 + 23y + 66 = 0
2y2 + 12y + 11y + 66 = 0
2y (y + 6) + 11(y + 6) = 0
(2y + 11) (y + 6) = 0
Y = -11/2, -6 = -5.5, -6
X > y
Direction (6-10) :
6) Answer: d)
Total number of successful candidates of IAS examination from state S
= > 5000*(26/100) = 1300
Total number of candidates appeared for IAS examination from state P
= > 90000*(24/100) = 21600
Required % = (1300/21600)*100 = 6 %
7) Answer: a)
The total number of candidates appeared for IAS examination from state Q and S together
= > [(21 + 16)/100]*90000 = 33300
The total number of successful candidates of IAS examination from state P, Q, R and T together
= > [(22 + 15 + 17 + 20)/100]*5000 = 3700
Required ratio = 33300: 3700 = 333: 37 = 9 : 1
8) Answer: c)
The total number of unsuccessful candidates of State R
= > [90000*(19/100)] – [5000*(17/100)]
= > 17100 – 850 = 16250
The total number of unsuccessful candidates of State S
= > [90000*(16/100)] – [5000*(26/100)]
= > 14400 – 1300 = 13100
Required difference = 16250 – 13100 = 3150
9) Answer: b)
The total number of unsuccessful candidates of State P, Q and R together
= > {[90000*(24/100)] – [5000*(22/100)]} + {[90000*(21/100)] – [5000*(15/100)]} + {[90000*(19/100)] – [5000*(17/100)]}
= > (21600 – 1100) + (18900 – 750) + (17100 – 850)
= > 20500 + 18150 + 16250
= > 54900
Required average = 54900/3 = 18300
10) Answer: d)
Required % = [(45 – 36)/36]*100
= > 25 %





