Dear Readers, Bank Exam Race for the Year 2019 is already started, To enrich your preparation here we have providing new series of Practice Questions on Quantitative Aptitude – Section. Candidates those who are preparing for NIACL AO Mains 2019 Exams can practice these questions daily and make your preparation effective.
[WpProQuiz 5316]
Click here to take NIACL AO Mock Test
Directions (Q. 1 – 5): In the following questions, two equations I and II are given. You have to solve both the equations and give answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established
1)
I) 2x2 + 25x + 57 = 0
II) 3y2 + 23y + 44 = 0
2)
I) x2 = 558 ÷ 3 × 2 + 112 – 9
II) y3 = 6859
3)
I) x2 – 24x – 81 = 0
II) y2 + y – 56 = 0
4)
I) 4x – 7y = 23
II) 3x – 5y = 16
5)
I) 9x2 – 26x + 16 = 0
II) 3y2 – 16y + 20 = 0
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following table shows the total number of people appointed for six different specialist posts by five different banks in a certain year in a state.
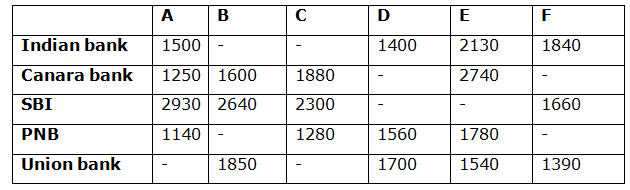
6) Find the difference between the total number of people appointed for the posts A, C and E together for Indian bank to that of total number of people appointed for the posts B, D and F together for Indian bank, if the total number of people appointed for the posts B and C for Indian bank is 15 % and 50 % more than the total number of people appointed for the post A for Indian bank respectively?
a) 1156
b) 1243
c) 915
d) 1028
e) None of these
7) Find the ratio between the total number of people appointed for the post A to that of post E for all the given banks together, if the total number of people appointed for the post A for union bank is 800 less than the total number of people appointed for the post A for SBI and the ratio between the total number of people appointed for the post A for Indian bank to that of post E for SBI is 3 : 5?
a) 895: 1069
b) 142: 257
c) 356: 515
d) 27: 89
e) None of these
8) Total number of people appointed for the post A, B and C together for Canara bank is approximately what percentage of total number of people appointed for the post D, E and F together for Union bank?
a) 78 %
b) 86 %
c) 115 %
d) 102 %
e) 127 %
9) If the average number of people appointed for all the given specialist post for PNB is 1510 and the total number of people appointed for the post B is 540 less than the total number of people appointed for the post F, then find the total number of people appointed for the post F for PNB?
a) 1850
b) 1920
c) 1740
d) 1660
e) None of these
10) Total number of people appointed for the post C for Canara bank, SBI and PNB together is what percentage more/less than the total number of people appointed for the post F for Indian bank, SBI and Union bank together?
a) 15.78 % less
b) 8.53 % more
c) 11.65 % more
d) 14.32 % less
e) None of these
Answers :
Direction (1-5) :
1) Answer: e)
I) 2x2 + 25x + 57 = 0
2x2 + 6x + 19x + 57 = 0
2x (x + 3) + 19 (x + 3) = 0
(2x + 19) (x + 3) = 0
X = -19/2, -3 = -9.5, -3
II) 3y2 + 23y + 44 = 0
3y2 + 12y + 11y + 44 = 0
3y (y + 4) + 11 (y + 4) = 0
(3y + 11) (y + 4) = 0
Y = -11/3, -4 = -3.66, -4
Can’t be determined
2) Answer: e)
I) x2 = 558 ÷ 3 × 2 + 112 – 9
X2 = (558/3)*2 + 121 – 9
X2 = 372 + 121 – 9 = 484
X = 22, -22
II) y3 = 6859
Y = ∛6859 = 19
Can’t be determined
3) Answer: e)
I) x2 – 24x – 81 = 0
(x – 27) (x + 3) = 0
X = 27, -3
II) y2 + y – 56 = 0
(y + 8) (y – 7) = 0
Y = -8, 7
Can’t be determined
4) Answer: a)
4x – 7y = 23 —-> (1)
3x – 5y = 16 —-> (2)
By solving (1) and (2), we get,
X = -3, y = -5
X > y
5) Answer: d)
I) 9x2 – 26x + 16 = 0
9x2 – 18x – 8x + 16 = 0
9x (x – 2) – 8 (x – 2) = 0
(9x – 8) (x – 2) = 0
X = 8/9, 2
II) 3y2 – 16y + 20 = 0
3y2 – 6y – 10y + 20 = 0
3y (y – 2) – 10 (y – 2) = 0
(y – 2) (3y – 10) = 0
Y = 2, 10/3
X ≤ y
Direction (6-10) :
6) Answer: c)
The total number of people appointed for the posts A, C and E together
= > 1500 + 1500*(150/100) + 2130
= > 1500 + 2250 + 2130 = 5880
The total number of people appointed for the posts B, D and F together
= > 1500*(115/100) + 1400 + 1840
= > 1725 + 1400 + 1840 = 4965
Required difference = 5880 – 4965 = 915
7) Answer: a)
Total number of people appointed for the post A for all the given banks together
= > 1500 + 1250 + 2930 + 1140 + (2930 – 800)
= > 8950
Total number of people appointed for the post E for all the given banks together
= > 2130 + 2740 + (1500*5/3) + 1780 + 1540
= > 10690
Required ratio = 8950: 10690 = 895: 1069
8) Answer: d)
Total number of people appointed for the post A, B and C together for Canara bank
= > 1250 + 1600 + 1880 = 4730
Total number of people appointed for the post D, E and F together for Union bank
= > 1700 + 1540 + 1390 = 4630
Required % = (4730/4630)*100 = 102 %
9) Answer: b)
The total number of people appointed for all the given specialist post for PNB
= 1510*6 = 9060
= > 1140 + B + 1280 + 1560 + 1780 + F = 9060
= > B + F = 9060 – 5760
= > B + F = 3300 —à (1)
The total number of people appointed for the post B = The total number of people appointed for the post F – 540
B = F – 540
= > F – B = 540 —à (2)
By solving the equation (1) and (2), we get,
F = 1920, B = 1380
The total number of people appointed for the post F for PNB = 1920
10) Answer: c)
Total number of people appointed for the post C for Canara bank, SBI and PNB together
= > 1880 + 2300 + 1280 = 5460
Total number of people appointed for the post F for Indian bank, SBI and Union bank together
= > 1840 + 1660 + 1390 = 4890
Required % = [(5460 – 4890)/4890]*100 = 11.65 % more





