Dear Readers, Bank Exam Race for the Year 2018 is already started, To enrich your preparation here we have providing new series of Practice Questions on Quantitative Aptitude – Section. Candidates those who are preparing for NIACL AO Prelims 2018 Exams can practice these questions daily and make your preparation effective.
[WpProQuiz 4757]
Click here to take NIACL AO Mock Test
Click here to View Quantitative Aptitude Questions in Hindi
1) Rajeev borrowed a certain amount at the rate of 12 % per annum and pays a simple interest of Rs. 30720 at the end of 4 years. What amount of compound interest would he pay on the same amount at the same rate of interest at the end of 3 years?
a) Rs. 25915.392
b) Rs. 23857.128
c) Rs. 24564.456
d) Rs. 27893.521
e) None of these
2) P, Q and R started business by investing in the ratio of 5: 3: 7. After 4 months, P invested 20 % more than the initial investment and R withdraw three- seventh of the initial investment. Find the total profit at the end of the year, if the share of Q is Rs. 13383?
a) Rs. 51323
b) Rs. 45865
c) Rs. 60967
d) Rs. 57631
e) None of these
3) A man can row 25 km/hr in still water and the river is running at 13 km/hr. If the man takes 5 hrs to row to a place and back, then how far is the place?
a) 40.8 km
b) 42.4 km
c) 45.6 km
d) 46.2 km
e) None of these
4) The percentage profit earned when the article is sold for Rs. 546 is double the percentage profit earned when the same article is sold for Rs. 383. If the marked price of the article is 40 % above the cost price, then find the marked price of the article?
a) Rs. 324
b) Rs. 252
c) Rs. 276
d) Rs. 308
e) None of these
5) 120 m length of Train A crosses another train B travelling in opposite direction in 15 seconds. Train A crosses a pole in 15 sec and the length of train A is half of the length of train B then find the speed of train B in?
a) 16 m/s
b) 22 m/s
c) 28 m/s
d) 24 m/s
e) None of these
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following pie chart shows the total number of students (both higher secondary and graduation) studying a different course from different institutions and the table shows the ratio of higher secondary students to that of graduation students from different institutions.
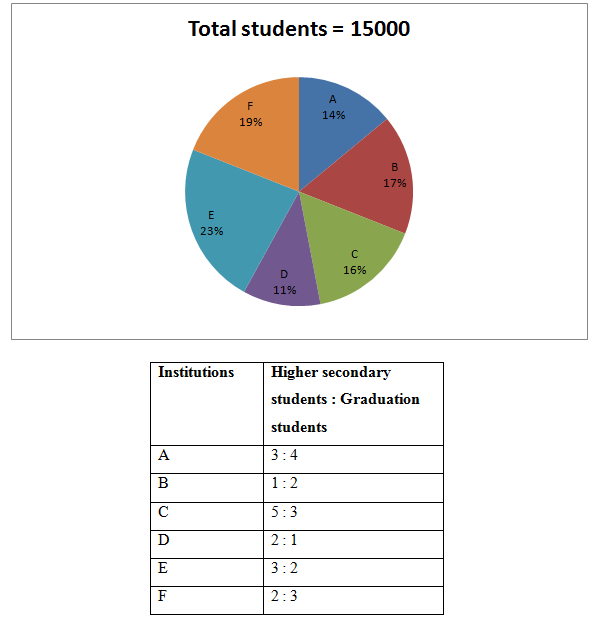
6) Find the ratio between the total number of graduate students from institution A and C together to that of total number of higher secondary students from institution B and D together?
a) 15: 11
b) 23: 17
c) 14: 13
d) 22: 19
e) None of these
7) Find the difference between the total number of higher secondary students from institution A to that of total number of graduate students from institution D?
a) 350
b) 420
c) 280
d) 240
e) None of these
8) Find the total number of graduate students from institution D, E and F together?
a) 3320
b) 3850
c) 2930
d) 3640
e) None of these
9) If the ratio of total number of male to that of female graduates from institution C is 8 : 7, then find the sum of the total number of male graduates from institution C and total number of higher secondary students from institution F together?
a) 1850
b) 1620
c) 2160
d) 2380
e) None of these
10) Which of the following institution has second lowest number of higher secondary students?
a) Institution A
b) Institution B
c) Institution C
d) Institution D
e) Institution E
Answers:
1) Answer: a)
S.I = PNR/100
30720 = (P*12*4)/100
P = (3072000)/48 = Rs. 64000
C. I:
64000*(12/100) = 7680
71680*(12/100) = 8601.6
80281.6*(12/100) = 9633.792
C.I = 7680 + 8601.6 + 9633.792 = Rs. 25915.392
2) Answer: c)
The share of P, Q and R
= > [5*4 + 5*(120/100)*8]: [3*12]: [7*4 + 7*(4/7)*8]
= > 68: 36: 60
= > 17: 9: 15
The share of Q = Rs. 13383
9’s = 13383
1’s = 13383/9 = 1487
Total profit = 41’s = Rs. 60967
3) Answer: c)
Downstream speed = (25+13) = 38 km/hr
Upstream speed = (25 – 13) = 12 km/hr
Let us take the distance be x
x/38 + x/12 = 5
(12+38)x = 5*12*38
50x = 5*12 *38
= > x = 45.6 km
(Or)
Let the still water and stream be x and y,
Distance = Time*[(x2 – y2)/2x]
= > 5*[(252 – 132)/(2*25)]
= > 5*[(625 – 169)/50]
= > 5*(456/50)
= > 45.6 km
4) Answer: d)
According to the question,
SP1 – CP = 2*(SP2 – CP)
546 – CP = 2*(383 – CP)
546 – CP = 766 – 2CP
CP = Rs. 220
MP = (140/100)*220 = Rs. 308
5) Answer: a)
Let the speed of train B be x,
Length of Train A = 120 m
Length of Train B = 240 m
T = D/S
{(120 + 240) / [(120/15) + x]} = 15
360/(8 + x) = 15
24 = 8 + x
X = 24 – 8 = 16 m/s
Directions (Q. 6 – 10):
6) Answer: c)
The total number of graduate students from institution A and C together
= > 15000*(14/100)*(4/7) + 15000*(16/100)*(3/8)
= > 1200 + 900 = 2100
The total number of higher secondary students from institution B and D together
= > 15000*(17/100)*(1/3) + 15000*(11/100)*(2/3)
= > 850 + 1100 = 1950
Required ratio = 2100: 1950 = 14: 13
7) Answer: a)
The total number of total number of higher secondary students from institution A
= > 15000*(14/100)*(3/7) = 900
The total number of total number of graduate students from institution D
= > 15000*(11/100)*(1/3) = 550
Required difference = 900 – 550 = 350
8) Answer: d)
The total number of graduate students from institution D, E and F together
= > 15000*(11/100)*(1/3) + 15000*(23/100)*(2/5) + 15000*(19/100)*(3/5)
= > 550 + 1380 + 1710 = 3640
9) Answer: b)
The ratio of total number of male to that of female graduates from institution C
= > 8: 7
The total number of male graduates from institution C
= > 15000*(16/100)*(3/8)*(8/15) = 480
The total number of higher secondary students from institution F
= > 15000*(19/100)*(2/5) = 1140
Required sum = 480 + 1140 = 1620
10) Answer: a)
Higher secondary students:
In institution A,
= > 15000*(14/100)*(3/7) = 900
In institution B,
= > 15000*(17/100)*(1/3) = 850
In institution C,
= > 15000*(16/100)*(5/8) = 1500
In institution D,
= > 15000*(11/100)*(2/3) = 1100
In institution E,
= > 15000*(23/100)*(3/5) = 2070
In institution F,
= > 15000*(19/100)*(2/5) = 1140
Institution A has second lowest number of higher secondary students.
Click here to take NIACL AO Mock Test
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| NIACL AO Prelims – Reasoning | 10.00 AM |
| NIACL AO Prelims – Reasoning (Hindi) | 10.30 AM |
| NIACL AO Prelims – Quantitative Aptitude | 11.00 AM |
| NIACL AO Prelims – Quantitative Aptitude (Hindi) | 11.30 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| NIACL AO Prelims – English Language | 1.00 PM |
| SSC Practice Questions (Reasoning/Quantitative aptitude) | 2.00 PM |
| IBPS Clerk – GK Questions | 3.00 PM |
| SSC Practice Questions (English/General Knowledge) | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| SBI PO/IBPS Clerk Mains – Reasoning | 6.00 PM |
| SBI PO/IBPS Clerk Mains – Quantitative Aptitude | 7.00 PM |
| SBI PO/IBPS Clerk Mains – English Language | 8.00 PM |





