SBI PO 2019 Notification will be expected soon. It is one of the most expected recruitment among the banking aspirants. Every year the exam pattern for SBI PO has been changing. Depends upon the changing of exam pattern the questions are quite harder compare to the previous year. So the questions are in high level than the candidate’s assumption.
As per the latest trend, our IBPS Guide is providing the updated New Exam Pattern Quantitative Aptitude questions for SBI PO 2019 Day 14. Our Skilled experts were mounting the questions based on the aspirant’s needs. So candidates shall start your preparation and practice on daily basis with our SBI PO pattern quantitative aptitude questions 2019 day 14. Start your effective preparation from the right beginning to get success in upcoming SBI PO 2019.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5248]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Directions (1 – 5): The questions below are based on the given Series-I. The series-I satisfy a certain pattern, follow the same pattern in Series-II and answer the questions given below.
1) I) 12, 16, 48, 180, 784
II) 5 ………. 616. If 616 is nth term, then what value should come in place of (n – 2)th term?
a) 56
b) 72
c) 68
d) 34
e) 30
2) I) 117, 122, 147, 272, 897, 4022
II) 21 ……… 801. If 801 is nth term, then what value should come in place of (n + 1)th term?
a) 3877
b) 3926
c) 3729
d) 3652
e) None of these
3) I) 8, 5, 7, 18, 80, 656
II) 14 ……… 848. If 848 is nth term, then find the value of n?
a) 8
b) 7
c) 6
d) 5
e) None of these
4) I) 118, 146, 176, 211, 256, 318
II) 52, 88 …….. 388. If 388 is nth term, then find the value of n?
a) 7
b) 6
c) 5
d) 8
e) None of these
5) I) 7, 17, 37, 77, 157, 317
II) 21 ……. 381. If 381 is nth term, then find the value of (n + 2)th term?
a) 1346
b) 1602
c) 1533
d) 765
e) 1428
Directions (Q. 6 – 10) Study the following information carefully and answer the given questions:
The following pie chart shows the total number of Lenovo mobile phones sold by a shopkeeper in different months and the table shows the ratio of Lenovo and Acer mobile phones sold in the given months.
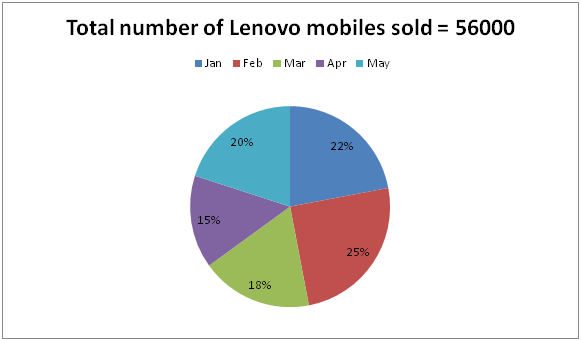
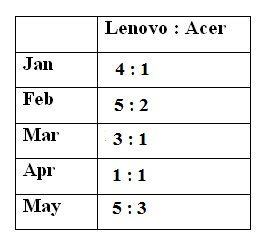
6) Total number of Lenovo mobiles sold in the month of Jan and Feb together is approximately what percentage of the total number of Acer mobiles sold in the same months?
a) 303 %
b) 247 %
c) 188 %
d) 152 %
e) 276 %
7) Find the difference between the total number of Acer mobiles sold in the month of Mar to that of May?
a) 5180
b) 4620
c) 4230
d) 3360
e) None of these
8) Find the ratio between the total number of Lenovo mobiles sold in the month of Jan and Mar together to that of Apr and May together?
a) 3 : 5
b) 5 : 9
c) 8 : 7
d) 11 : 15
e) None of these
9) Find the total number of Acer mobiles sold in the month of Jan, Feb and Apr together?
a) 13060
b) 17080
c) 14020
d) 15010
e) None of these
10) The total number of Lenovo mobiles sold in the month of Feb is what percentage of the total number of Lenovo mobiles sold in the months of May?
a) 75 %
b) 90 %
c) 100 %
d) 115 %
e) 125 %
Answers :
Direction (1-5) :
1) Answer: d)
Series I,
12 is the first term
12 *1 + 22 = 16
16 *2 + 42 = 48
48 *3 + 62 = 180
180 *4 + 82 = 784
784 is 5th term
Series II,
5 is the first term.
5*1 + 22 = 9
9*2 + 42 = 34
34*3 + 62 = 138
138*4 + 82 = 616
616 is 5th term. n = 5
So, (n – 2)th term = 34
2) Answer: b)
Series I,
117 is the first term
117 + 51 = 122
122 + 52 = 147
147 + 53 = 272
272 + 54 = 897
897 + 55 = 4022
4022 is 6th term
Series II,
21 is the first term
21 + 51 = 26
26 + 52 = 51
51 + 53 = 176
176 + 54 = 801
801 + 55 = 3926
801 is 5th term. (n + 1)th term, ie., 6th term is 3926
3) Answer: c)
Series I,
8 is the first term,
8*0.5 + 1 = 5
5*1 + 2 = 7
7*2 + 4 = 18
18*4 + 8 = 80
80*8 + 16 = 656
656 is 6th term
Series II,
14 is the first term,
14*0.5 + 1 = 8
8*1 + 2 = 10
10*2 + 4 = 24
24*4 + 8 = 104
104*8 + 16 = 848
848 is 6th term
4) Answer: a)
Series I,
118 is the first term. 318 is 6th term
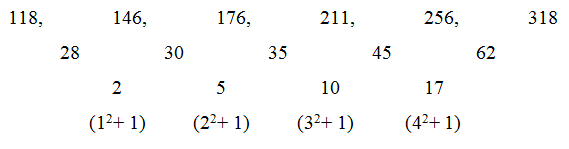
Series II,
52 is the first term. 388 is 7th term
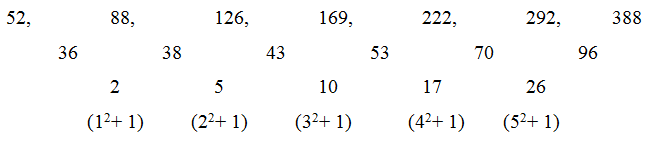
5) Answer: c)
Series I,
7 is the first term
7*2 + 3 = 17
17*2 + 3 = 37
37*2 + 3 = 77
77*2 + 3 = 157
157*2 + 3 = 317
317 is 6th term
Series II,
21 is the first term
21*2 + 3 = 45
45*2 + 3 = 93
93*2 + 3 = 189
189*2 + 3 = 381
381*2 + 3 = 765
765*2 + 3 = 1533
381 is 5th term. (n + 2)th term (ie)., 7th term = 1533
Direction (6-10) :
6) Answer: a)
Total number of Lenovo mobiles sold in the month of Jan and Feb together
= > 56000*(22/100) + 56000*(25/100)
= > 12320 + 14000 = 26320
Total number of Acer mobiles sold in the month of Jan and Feb together
= > 56000*(22/100)*(1/4) + 56000*(25/100)*(2/5)
= > 3080 + 5600 = 8680
Required % = (26320/8680)*100 = 303 %
7) Answer: d)
The total number of Acer mobiles sold in the month of Mar
= > 56000*(18/100)*(1/3) = 3360
The total number of Acer mobiles sold in the month of May
= > 56000*(20/100)*(3/5) = 6720
Required difference = 6720 – 3360 = 3360
8) Answer: c)
The total number of Lenovo mobiles sold in the month of Jan and Mar together
= > 56000*[(22 + 18)/100]
The total number of Lenovo mobiles sold in the month of Apr and May together
= > 56000*[(15 + 20)/100]
Required ratio = [(56000/100)*40] : [(56000/100)*35]
= > 40 : 35 = 8 : 7
9) Answer: b)
The total number of Acer mobiles sold in the month of Jan, Feb and Apr together
= > 56000*(22/100)*(1/4) + 56000*(25/100)*(2/5) + 56000*(15/100)*(1/1)
= > 3080 + 5600 + 8400 = 17080
10) Answer: e)
Required % = (25/20)*100 = 125 %





