SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5313]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Study the following information carefully and answer the questions given below:
The following table represents number of doctors, singers, dancers and engineers in six different groups.
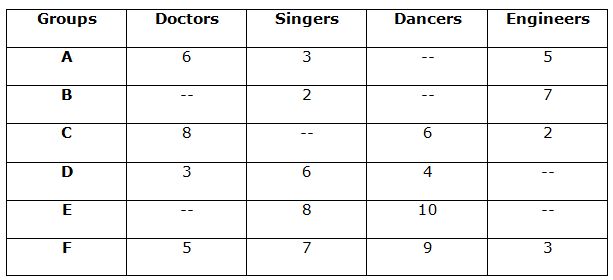
1) A committee of five members is to be formed from group A such that the committee contains one member from each of the given four professions and remaining one member can be anyone from the given four professions. The number of ways in which this can be possible is 5040. Find the probability of selecting 2 doctors and 2 dancers from group A.
a) 1/38
b) 1/34
c) 1/36
d) 1/42
e) None of these
2) Probability of selecting one doctor from group E is 3/8 and probability of selecting one singer from group E is ¼. A committee of four members is to be formed from group E such that the committee contains 2 doctors, 1 singer and 1 dancer. Find the number of ways in which this can be possible.
a) 5280
b) 4040
c) 6040
d) 3020
e) None of these
3) A committee of six members is to be formed from group C such that the committee contains 2 doctors, 1 singer, 2 dancers and 1 engineer. The number of ways in which this can be possible is 2520. Find the respective ratio of the probability of selecting 2 singers from group C and probability of selecting 2 singers from group F.
a) 73:543
b) 67:298
c) 55:321
d) 92:399
e) None of these
4) Probability of selecting one doctor from group B is 2/9 and probability of selecting 1 singer from that group is 1/9.
Quantity I: A committee of five members is to be formed such that the committee contains 2 doctors, 1 singer, 1 dancer and 1 engineer. Find the number of ways in which this can be done.
Quantity II: A committee of five members is to be formed such that the committee contains 1 doctor, 2 singers and 2 dancers. Find the number of ways in which this can be done.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II or no relation can be established.
5) Find the respective ratio of total number of persons in group D and total number of persons in group F.
Statement I: Probability of selecting one doctor from group D is 1/6.
Statement II: A committee of four members is to be formed from group D such that the committee contains one member from each of the given four professions. The number of ways in which this can be possible is 360.
a) Statement I alone is sufficient to answer the question, but the statement II alone is not sufficient.
b) Statement II alone is sufficient to answer the question, but the statement I alone is not sufficient.
c) Either statement I alone or statement II alone is sufficient to answer the question.
d) Both statements I and II together are needed to answer the question.
e) Both statements I and II together are not sufficient to answer the question.
Directions (6 – 10): Study the following information carefully and answer the questions given below:
The following table represents information regarding six different fields.
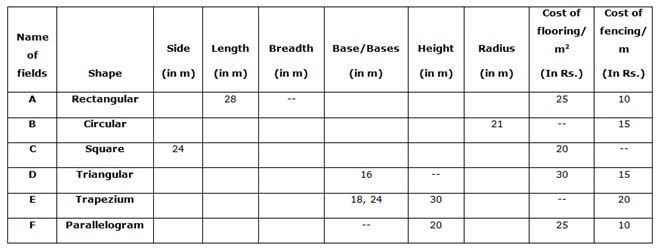
6) If total cost of flooring of field A is Rs.15400 and total cost of flooring of field D is Rs.5760, find the respective ratio of total cost of fencing of field A and total cost of fencing of field D.
a) 2: 3
b) 5: 8
c) 3: 5
d) Cannot be determined
e) None of these
7) If total cost of flooring of field B is Rs.34650 and total cost of flooring of field E is Rs.12600, cost of flooring/m2 of field B is what percent of the cost of flooring/m2 of field E?
a) 110%
b) 125%
c) 75%
d) 100%
e) None of these
8) Total cost of flooring of field F is Rs.15000 and measure of another pair of parallel sides of field F is 24m. Cost of fencing/m of field C is Rs.12/m. Find the average of the cost of fencing of field C and cost of fencing of field F.
a) Rs.986
b) Rs.1020
c) Rs.1148
d) Rs.1116
e) None of these
9) Find the relation between following two quantities.
Quantity I: If cost of fencing field A is Rs.920, find the total cost of flooring of field A.
Quantity II: Field G is circular in shape and its radius is 7 m more than the radius of field B. If cost of flooring/m2 of field G is Rs.8, find the total cost of flooring of field G.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
10) Find the total cost of flooring of field H.
Statement I: Field H is rectangular in shape. Total cost of fencing of field H is Rs.960.
Statement II: Length of field H is 4 m more than its breadth. Cost of flooring/m2 of field H is Rs.22. Cost of fencing/m of field H is Rs.15.
a) Statement I alone is sufficient to answer the question, but the statement II alone is not sufficient.
b) Statement II alone is sufficient to answer the question, but the statement I alone is not sufficient.
c) Either statement I alone or statement II alone is sufficient to answer the question.
d) Both statements I and II together are needed to answer the question.
e) Both statements I and II together are not sufficient to answer the question.
Answers:
Directions (1 – 5):
1) Answer: b)
Let, number of dancers in group A = n
Doctors = 6
Singers = 3
Engineers = 5
Total number of persons in the group = 6 + 3 + n + 5 = 14 + n
According to the question
6c1 x 3c1 x nc1 x 5c1 x (14 + n – 4)c1 = 5040
=> 6 x 3 x n x 5 x (10 + n)c1 = 5040
=> n x (10 + n) = 5040/90
=> n2 + 10n = 56
=> n2 + 10n – 56 = 0
=> n2 + 14n – 4n – 56 = 0
=> n(n + 14) – 4(n + 14) = 0
=> (n – 4)(n + 14) = 0
=> n = 4, -14 (not valid)
=> n = 4
Hence, Dancers = 4
Total number of persons in the group = 14 + 4 = 18
Required probability = (6c2 x 4c2)/18c4
= (15 x 6)/3060
= 1/34
2) Answer: a)
Let, number of doctors in group E = m
And number of engineers in group E = n
Singers = 8
Dancers = 10
Total number of persons in group E = m + n + 8 + 10 = 18 + m + n
According to the question
m/(18 + m + n) = 3/8
=> 8m = 54 + 3m + 3n
=> 8m – 3m – 3n = 54
=> 5m – 3n = 54 —————– (i)
And
8/(18 + m + n) = ¼
=> 32 = 18 + m + n
=> m + n = 32 – 18
=> m + n = 14 ————- (ii)
Equation (i) + 3 x Equation (ii)
5m – 3n + 3m + 3n = 54 + 42
=> 8m = 96
=> m = 12
From (ii)
12 + n = 14
=> n = 14 – 12
=> n = 2
Hence, Doctors = 12
Engineers = 2
Required number of ways = 12c2 x 8c1 x 10c1
= 66 x 8 x 10
= 5280
3) Answer: d)
Let, number of singers in group C = n
Doctors = 8
Dancers = 6
Engineers = 2
Total number of persons in group C = n + 8 + 6 + 2 = 16 + n
According to the question
8c2 x nc1 x 6c2 x 2c1 = 2520
=> 28 x n x 15 x 2 = 2520
=> n = 2520/840
=> n = 3
Singer = 3
Total number of persons in group C = 16 + 3 = 19
Probability of selecting 2 singers from group C = 3c2/19c2
= 3/171
= 1/57
Probability of selecting 2 singers from group F = 7c2/24c2
= 21/276
= 7/92
Required ratio = 1/57: 7/92 = 92:399
4) Answer: a)
Let, number of doctors in group B = m
And number of dancers in group B = n
Singers = 2
Engineers = 7
Total number of persons in group B = m + n + 2 + 7 = 9 + m + n
m/(9 + m + n) = 2/9
=> 9m = 18 + 2m + 2n
=> 9m – 2m – 2n = 18
=> 7m – 2n = 18 ————— (i)
And
2/(9 + m + n) = 1/9
=> 18 = 9 + m + n
=> m + n = 18 – 9
=> m + n = 9 —————- (ii)
Equation (i) + 2 x Equation (ii)
7m – 2n + 2m + 2n = 18 + 18
=> 9m = 36
=> m = 4
From (ii)
4 + n = 9
=> n = 9 – 4
=> n = 5
Doctors = 4
Dancers = 5
Total number of persons in group B = 9 + 4 + 5 = 18
Quantity I:
Required number of ways = 4c2 x 2c1 x 5c1 x 7c1
= 6 x 2 x 5 x 7
= 420
Quantity II:
Required number of ways =4c1 x 2c2 x 5c2
= 4 x 1 x 10
= 40
Hence, Quantity I > Quantity II
5) Answer: c)
Let, number of engineers in group D = n
Doctors = 3
Singers = 6
Dancers = 4
Total number of persons in group D = n + 3 + 6 + 4 = 13 + n
From I:
3/(13 + n) = 1/6
=>18 = 13 + n
=> n = 18 – 13
=> n = 5
Required ratio = (3 + 6 + 4 + 5): (5 + 7 + 9 + 3)
= 18: 24
= 3:4
From II:
3c1 x 6c1 x 4c1 x nc1 = 360
=> 3 x 6 x 4 x n = 360
=> n = 360/72
=> n = 5
Required ratio = (3 + 6 + 4 + 5): (5 + 7 + 9 + 3)
= 18: 24
= 3:4
Hence, either statement I alone or statement II alone is sufficient to answer the question.
Directions (6 – 10):
6) Answer: d)
Area of field A = 15400/25 = 616 m2
We know that
Area of a rectangle = length x breadth
=> 616 = 28 x breadth
=> Breadth = 616/28
=> Breadth = 22 m
We know that
Perimeter of rectangle = 2 x (length + breadth)
= 2 x (28 + 22)
= 2 x 50
= 100 m
Cost of fencing of field A = 100 x 10 = Rs.1000
Area of field D = 5760/30 = 192 m2
We know that
Area of a triangle = ½ x base x height
=> 192 = ½ x 16 x height
=> Height = 192 x 2/16
=> Height = 24 m
But sides of the triangle are not known, hence, cost of fencing cannot be find out and required ratio cannot be find out.
7) Answer: b)
We know that
Area of a circle = πr2
=> Area of field B = 22/7 x 21 x 21 = 1386 m2
Cost of flooring/m2 of field B = 34650/1386 = Rs.25
We know that
Area of trapezium = ½ x (sum of the bases) x height
=> Area of field E = ½ x (18 + 24) x 30
= ½ x 42 x 30
= 630 m2
Cost of flooring/m2 of field E = 12600/630 = Rs.20
Required percentage = 25/20 x 100 = 125%
8) Answer: d)
Area of field F = 15000/25 = Rs.600
We know that
Area of parallelogram = base x height
=> 600 = base x 20
=> Base = 600/20
=> Base = 30 m
Perimeter of field F = 2 x (30 + 24)
= 2 x 54
= 108 m
Cost of fencing of field F = 108 x 10 = Rs.1080
We know that
Perimeter of a square = 4 x side
= 4 x 24
= 96 m
Cost of fencing of field C = 96 x 12 = Rs.1152
Required average = (1080 + 1152)/2
= 2232/2
= Rs.1116
e) Quantity I = Quantity II or no relation can be established.
9) Answer: b)
Quantity I:
Perimeter of field A = 920/10 = 92 m
We know that
Perimeter of a rectangle = 2 x (length + breadth)
=> 92 = 2 x (28 + breadth)
=> 28 + breadth = 92/2
=> Breadth = 46 – 28
=> Breadth = 18 m
We know that
Area of rectangle = length x breadth
= 28 x 18
= 504 m2
Total cost of flooring of field A = 504 x 25 = Rs.12600
Quantity II:
Radius of field G = 21 + 7 = 28 m
We know that
Area of circle = πr2
=> Area of field G = 22/7 x 28 x 28 = 2464 m2
Total cost of flooring of field G = 2464 x 8 = Rs.19712
Hence, Quantity I < Quantity II
10) Answer: d)
From I:
Field H is rectangular in shape. Total cost of fencing of field H is Rs.960.
From II:
Length of field H is 4 m more than its breadth. Cost of flooring/m2 of field H is Rs.22.
From I and II:
Let, breadth of field H = b m
=> Length = (b + 4) m
Perimeter of field H = 960/15 = 64 m
We know that
Perimeter of a rectangle = 2 x (length + breadth)
=> 64 = 2 x (b + 4 + b)
=> 2b + 4 = 64/2
=> 2b = 32 – 4
=> b = 28/2
=> b = 14
Hence, breadth = 14 m
Length = 14 + 4 = 18 m
We know that
Area of rectangle = length x breadth
=> Area of field H = 18 x 14 = 252 m2
Total cost of flooring of field H = 252 x 22 = Rs.5544
Hence, both statements I and II together are needed to answer the question.





