Dear Aspirants, the most awaited notification of SBI PO – 2019 has been released. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5822]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Based on the given passage, answer the questions that follow.
A invested Rs. 50000 in a company in the beginning of the year. After few months, B invested Rs. 40000 in the same company. At the end of the year, A received Rs. 12000 as his share of profit for the year. In the next year, A and B again invested the same amount as they did in the previous year for the whole year. After 3 months, C invested Rs. 60000 and received Rs. 4500 as his share of profit at the end of second year.
1) In the third year, if A, B and C invested the same amount as before in the second of the year, what is C’s share in a profit of Rs. 60000?
a) Rs. 12000
b) Rs. 18000
c) Rs. 24000
d) Rs. 32000
e) Rs. 36000
2) What is the share of A in the profit in the second year?
a) Rs. 3000
b) Rs. 3500
c) Rs. 4000
d) Rs. 5000
e) Rs. 5500
3) If B invested in the company after 4 months, what is the ratio of the share in profit of A and B?
a) 5 : 4
b) 5 : 8
c) 8 : 5
d) 15 : 4
e) 15 : 8
4) If B received Rs. 5600 as his share of profit at the end of first year, after how many months did he invested in the company?
a) 3
b) 4
c) 5
d) 6
e) 7
5) At the end of the first year, what amount did B received as his share of profit?
a) Rs. 6000
b) Rs. 9600
c) Rs. 10000
d) Rs. 12000
e) Couldn’t be determined
Directions (6 – 10): Read the following information carefully and answer the given questions.
There are total 1800 students in a class. Each students like one or more subjects among three subjects viz. Maths, Physics and Chemistry.
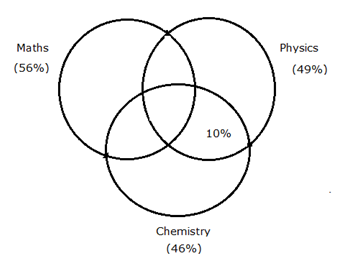
Boys: 56% of the total boys like Maths. 49% of the total boys like Physics. 46% of the total boys like Chemistry. 10% of the boys like Physics and Chemistry both but not Maths.
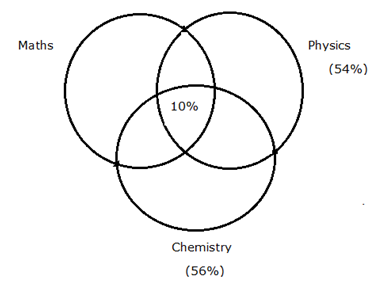
Girls: 54% of the total girls like Physics. Percentage of the total boys like Maths is same as the percentage of the girls like Chemistry. 10% of the total girls like all the three subjects.
6) If 5% of the total boys like all the three subjects and the number of boys like all the three subjects is same as the number of girls like all the three subjects.
Quantity I: A group of four students is to be formed from 12.5% of the total boys like Maths. Find the number of ways in which this can be possible.
Quantity II: A group of four students is to be formed from 25% of the total girls like Chemistry. Find the number of ways in which this can be possible.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II (or) Relationship cannot be established
7) A group of two students is to be formed from the total girls who like at most two subjects. Find the number of ways in which this can be possible.
Statement I: The number of boys like Physics is 264 more than the number of girls like Physics.
Statement II: Number of boys and girls like all the three subjects is same.
a) Only I
b) Only II
c) Either I or II
d) Neither I nor II
e) Both I and II
8) A group of four students is to be formed from the total boys such that the group contains 2 students who like Maths and Chemistry but not Physics and 2 students who like Maths and Physics but not Chemistry. Find the number of ways in which this can be possible if 5% of boys like all the three subjects which is 60 and 16% of the boys like only Chemistry.
a) 99*180*95*189
b) 84*179*191*90
c) 90*179 *96*191
d) Cannot be determined
e) None of these
9) Find the difference between the total number of boys like only two subjects and the total number of girls like only two subjects.
Statement I: The number of boys like Chemistry is 216 more than the number of girls like Chemistry.
Statement II: Number of boys and number of girls all the three subjects is same.
a) Only I
b) Only II
c) Either I or II
d) Both I and II
e) Neither I nor II
10) Number of girls like all the three subjects is 60, find the ratio of the total number of girls like more than one subject to the total number of boys like only one subject
Statement I: Total number of girls like only one subject is 336.
Statement II: 5% of boys like all the three subjects and 16% of the boys like only Chemistry.
a) Only I
b) Only II
c) Both I and II
d) Either I or II
e) Neither I nor II
Answers :
Direction (1-5) :
1) Answer: c)
In third year,
A’s investment = Rs. 50000 for 12 months
B’s investment = Rs. 40000 for 12 months
C’s investment = Rs. 60000 for 12 months
Hence,
⇒ A’s share : B’s share : C’s share = 50000 : 40000 : 60000
⇒ A’s share : B’s share : C’s share = 5 : 4 : 6
∴ C’s share = (6/15) × 60000 = Rs. 24000
2) Answer: d)
In second year,
A’s investment = Rs. 50000 for 12 months
C’s investment = Rs. 60000 for (12 – 3) = 9 months
C’s share = Rs. 4500
Hence,
⇒ (50000 × 12) : (60000 × 9) = A’s share : 4500
⇒ 10 : 9 = A’s share : 4500
⇒ A’s share = (10/9) × 4500
∴ A’ share = Rs. 5000
3) Answer: e)
A’s investment = Rs. 50000 for 12 months
B’s investment = Rs. 40000 for (12 – 4) = 8 months
∴ Ratio of their share in profit = (50000 × 12) : (40000 × 8) = 15 : 8
4) Answer: c)
Let B invested in the company after ‘x’ months
A’s investment = Rs. 50000 for 12 months
B’s investment = Rs. 40000 for (12 – x) months
A’s share = Rs. 12000
B’s share = Rs. 5600
Hence,
⇒ (50000 × 12) : [40000 × (12 – x) ] = 12000 : 5600
⇒ (5 × 12) : [4 × (12 – x) ] = 120 : 56
⇒ 60 : (48 – 4x) = 120 : 56
⇒ (60 × 56)/120 = 48 – 4x
⇒ 28 = 48 – 4x
⇒ 4x = 20
⇒ x = 5
∴ B invested in the company after 5 months
5) Answer: e)
As the time duration for which B invested his money is not known, his share of profit couldn’t be determined.
Directions (6 – 10):
Boys:
Girls:
6) Answer: e)
Let us take the number of girls be x and number of boys be (1800 – x)
According to the question,
5% of (1800 – x) = 10% of x
90 – 5x/100 = 10x/100
= > 90 = 15x/100
= > x = 600
Number of boys = 1800 – 600 = 1200
Quantity I: A group of four students is to be formed from 12.5% of the total boys like Maths. Find the number of ways in which this can be possible.
Total boys like Maths = 56/100*1200 = 672
12.5% of the total boys like Maths = 672 * 12.5/100
= 84
Total number of ways = 84C4
= (84*83*82*81)/(1*2*3*4)
= 1929501
Quantity II: A group of four students is to be formed from 25% of the total girls like Chemistry. Find the number of ways in which this can be possible.
Total girls like Chemistry = 600*56/100 = 336
25% of the total girls like Chemistry = 336*25/100 = 84
Total number of ways = 84C4
= (84*83*82*81)/(1*2*3*4)
= 1929501
Hence, Quantity I = Quantity II
7) Answer: a)
From statement I,
Let us take the number of girls be x and number of boys be (1800 – x)
According to the question,
49% of (1800 – x) – 264 = 54% of x
882 – 49x/100 – 264 = 54x/100
882 + 264 = 54x/100 + 49x/100
= > 618 = 103x/100
= > 6 = x/100
= > x = 600
Number of girls like at most two subjects = 600 – (10/100 * 600)
= 600 – 60 = 540
Required number of ways = 540C2
= 540*539/(1*2)
= 145530
Hence statement I alone is sufficient to answer the given question.
From statement II,
Let us take the number of girls be x and number of boys be (1800 – x)
Percentage of the boys like all the three subjects is z,
According to the question,
(1800 – x) * z/100 = x * 10/100
From that we cannot find the total girls
Hence statement II alone is not sufficient to answer the given question.
8) Answer: c)
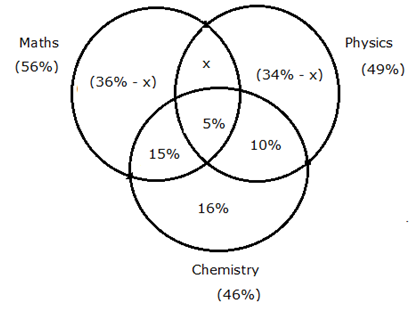
From the diagram,
(36% – x) + 5% + 15% + 10% + 16% + x + (34% -x) = 100%
116% – x = 100%
= > x = 16%
5% of total boys = 60
= > Total boys = 60 *(100/5) = 1200
Number of boys like Maths and Chemistry but not Physics = 15%
= 15/100 * 1200 = 180
Number of boys like Maths and Physics but not Chemistry = 16%
= 16/100 * 1200 = 192
Required number of ways = 180C2 * 192C2
= (180*179/1*2) * (192*191/1*2)
= 90*179 *96*191
9) Answer: e)
Statement I: The number of boys like Chemistry is 216 more than the number of girls like Chemistry.
From statement I,
Let us take the number of girls be x and number of boys be (1800 – x)
According to the question,
46% of (1800 – x) = 216 + 56% of x
828 – 46x/100 = 216 + 56x/100
= > 828 – 216 = 56x/100 + 46x/100
= > 612 = 102x/100
= > x = 600
From that, we know only total boys and total girls. We have to know the percentage of the students like only one subject.
Hence, statement I alone is not sufficient to answer the given question.
From statement II,
From that, we didn’t know the exact number of students like all the three subjects.
Hence, statement II alone is not sufficient to answer the given question.
10) Answer: c)
10% of total girls = 60
= > Total girls = 60 *(100/10) = 600
Total boys = 1800 – 600 = 1200
From statement I,
Total number of girls like more than one subject = 600 – 336 = 264
Hence, statement I alone is not sufficient to answer the given question.
Statement II: 5% of boys like all the three subjects and 16% of the boys like only Chemistry.
From statement II,
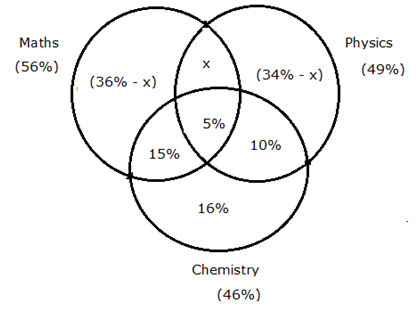
From the diagram,
(36% – x) + 5% + 15% + 10% + 16% + x + (34% -x) = 100%
116% – x = 100%
= > x = 16%
5% of total boys = 60
= > Total boys = 60 *(100/5) = 1200
Total boys like only one subject
= [(36% – 16%) + 16% + (34% – 16%)] * 1200
= (20% + 16% + 18%) *1200
= 54/100 * 1200
= 648
Hence, statement II alone is not sufficient to answer the given question.
From statement I and II,
Number of girls like more than one subject = 264
Number of boys like only one subject = 648
Required ratio = 264: 648
= 11: 27
Hence, statement I and II are necessary to answer the given question.





