Dear Aspirants, the most awaited notification of SBI PO – 2019 has been released. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 6069]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here o View Quantitative Aptitude Questions in Hindi
Direction (1 – 5): Study the following data carefully and answer the questions:
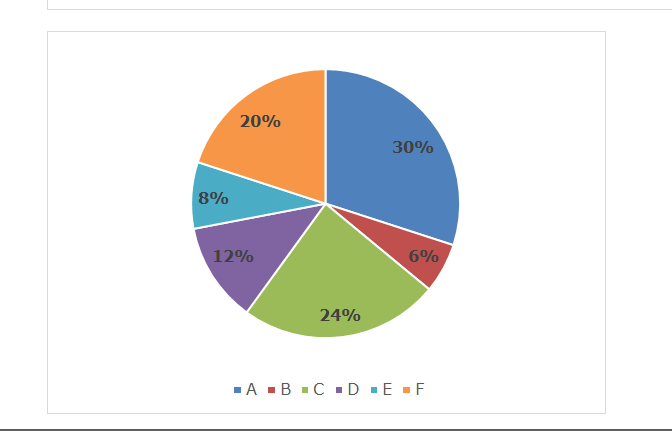
There are 6 inlet pipes P, Q, R, S, T and U and 6 outlet pipes A, B, C, D, E and F. Bar graph given below shows the time taken (hours) by 6 inlet pipes to fill a tank while the pie chart shows the per cent distribution of time taken (hours) by 6 outlet pipes to empty that tank.
Sum of the pie chart is 50 hours.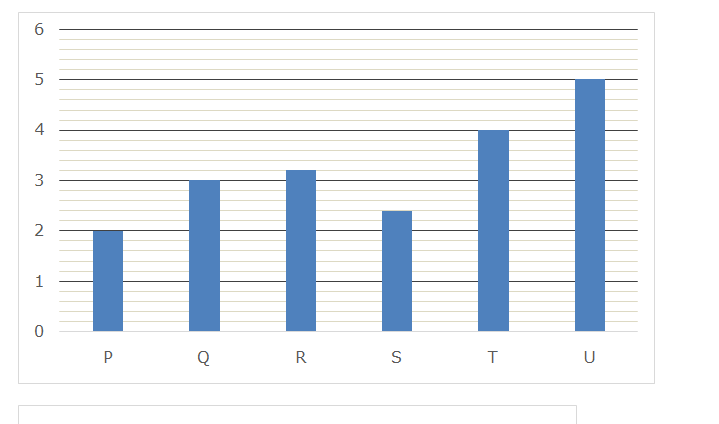
1) Time taken by pipes P and Q together to fill the tank when P is working with 80% of its original efficiency and pipe Q is working with 30% of its original efficiency is ‘T1’ and time taken by pipes P, Q and D together to fill that tank when all the pipes are working with its original efficiency is ‘T2’, then what is the difference between ‘T1’ and ‘T2’?
a) 45 minutes
b) 30 minutes
c) 50 minutes
d) 60 minutes
e) None of these
2) What is the total time taken by pipes U, A and F to fill the tank if all the three pipes are working alternatively for 1 hour each starting with pipe U followed by A and then by F? Assume pipe U is working with its efficiency 33(1/3)% more than its original efficiency, pipe F is working with half of its original efficiency and pipe A is working with its original efficiency?
a) 30 hours
b) 15 hours
c) 20 hours
d) 10 hours
e) None of these
3) Pipe T and C together start on the tank and after working for ‘N’ hours pipe T is replaced with pipe S and after working for 1 more hour pipe C is replaced with pipe D. Now, after working for 1 more hour pipe D stopped working and it takes 12 more minutes to fill the tank, then what is the value of ‘N’?
a) 2
b) 1.5
c) 3
d) 2.5
e) None of these
4) Two pipes R and E together can fill the tank in ‘N’ hours. If three pipes U, A and F together start filling that tank, then after how much time the pipe A should stop working so that total time taken to fill the tank in this arrangement is ‘N’ hours?
a) 6 hours
b) 7 hours
c) 8 hours
d) 9 hours
e) None of these
5) Three pipes R, S and D together start filling the tank and after working for 40 minutes pipe S is replaced by pipe C, then what is the total time taken by pipes R, C and D together to fill the remaining part of the tank?
a) 6 hours
b) 8 hours
c) 10 hours
d) 12 hours
e) None of these
6) The ratio of the present ages Ram to Sunil is 3:4 and the product of the ages of Sunil and Rahul is 864 years. If the ratio of the ages of Ram to Shon is 3:2 and the product of the ages of Shon and Sunil is 648 years.
From the statement given in the above question which of the following can be determined.
a) Age of Ram
b) Age of Rahul
c) If the ratio of the ages of Rahul to Surya is 4:3, then the age of Surya.
d) If the sum of the ages of Shon and Nitish is 30 years, then the age of Nitish.
a) All A, B, C and D
b) Only B and C
c) Only D and B
d) Only A
e) Cannot be determine
7) If the ratio of the radius of the circle to the cylinder is 1:2 and the height of the cylinder is 10 cm more than that of the radius of the cylinder. The radius of the cone and height is radius of the circle and height of the cylinder respectively and the circumference of the circle is 44 cm.
From the statement given in the above question which of the following can be determined.
a) Volume of the cylinder
b) Length of the cone
c) Curved surface area of the cone
d) Total surface area of the Cylinder
a) All A, B, C and D
b) Only B and C
c) Only D and B
d) Only A
e) Cannot be determine
8) France and Prince started the business with investment of Rs.x, and Rs.(x + 2000) respectively. After 4 months Sam joined with Rs.(x – 1000) and France added Rs.x for his initial investment. At the end of one year the total profit is Rs.12000 and the profit share of France is Rs.5000.
From the statement given in the above question which of the following can be determined.
a) Value of x
b) Profit share of Sam
c) Prince invests his profit share amount on simple interest for 5 years. Find the interest received by prince after 5 years.
d) Initial investment of Sam
a) All A, B, C and D
b) Only B and C
c) Only D and B
d) Only A and B
e) Only A, B and D
9) A boat can row —- km downstream and comeback to original position in —- hours and the ratio of the speed of the stream to boat is 2:3. The speed of the stream is —- kmph.
a) 40, 8, 16
b) 50, 10, 14
c) 60, 12, 12
d) 70, 14, 10
a) Only B
b) Only A, B
c) Only C
d) Only B, D
e) Only A
10) A milkman has —— liters of the mixture of milk and water in the ratio of 4:3. —- liters of mixture sold and it is replaced with 30 liters of milk and 15 liters of water. Now the ratio of the milk to water in the final mixture is 3:2.
a) 120 liters, 15 liters
b) 100 liters, 10 liters
c) 90 liters, 20 liters
d) 130 liters, 25 liters
a) Only B
b) Only A, B
c) Only C
d) Only A, D
e) Only A
Answers :
Directions (1 – 5):
Time taken by pipe A to empty the tank = 30% of 50 = 15 hours
Time taken by pipe B to empty the tank = 6% of 50 = 3 hours
Time taken by pipe C to empty the tank = 24% of 50 = 12 hours
Time taken by pipe D to empty the tank = 12% of 50 = 6 hours
Time taken by pipe E to empty the tank =8% of 50 = 4 hours
Time taken by pipe F to empty the tank = 20% of 50 = 10 hours
| Inlet Pipes | Time taken to fill the tank | Outlet pipes | Time taken to empty the tank |
| P | 2 hours | A | 15 hours |
| Q | 3 hours | B | 3 hours |
| R | 3.2 hours | C | 12 hours |
| S | 2.4 hours | D | 6 hours |
| T | 4 hours | E | 4 hours |
| U | 5 hours | F | 10 hours |
1) Answer: b)
Time taken by pipe P alone when working with 80% of its original efficiency
= 2 * (100/80) = 2.5 hours
Time taken by pipe Q alone when working with 30% of its original efficiency
= 3 * (100/30) = 10 hours
T1 = 1/[(1/2.5) + (1/10)]
T1 = 2 hours
Time taken by pipes P, Q and D together to fill that tank when all the pipes are working with its original efficiency = T2 = 1/[(1/2) + (1/3) – (1/6)]
T2 = 1.5 hours
Required difference = 2 – 1.5 = 0.5 hours = 30 minutes
2) Answer: c)
Time taken by pipe U alone to fill the tank when working with 33(1/3)% more than its original efficiency = 5 * (3/4) = 3.75 hours
Time taken by pipe F alone to empty the tank when working with 50% of its original efficiency = 10 * 2 = 20 hours.
Since, all the pipes are opened for 1 hour each, then part of tank filled in first 3 hours = (1/3.75) – (1/20) – (1/15) = (16 – 3 – 4)/60 = 9/60 = 3/20
Time taken to fill whole tank = (20/3) * 3 = 20 hours
3) Answer: a)
Time taken by pipes S and T alone to fill the tank is 2.4 hours and 4 hours respectively and time taken by pipes C and D alone to empty the tank is 12 hours and 6 hours respectively.
Let total capacity of the tank = 24 (LCM of 2.4, 4, 12 and 6)
Part of tank filled by pipes S and T in one hour is 10 and 6 respectively.
Part of tank emptied by pipes C and D in one hour is 2 and 4 respectively.
Part of tank filled in first N hours = N * (6 – 2) = 4N
Part of tank filled in next 2 hours 12 minutes
= (10 – 2) + (10 – 4) + 10 * (12/60)
= 8 + 6 + 2 = 16
According to the question:
4N + 16 = 24
4N = 8
N = 2
4) Answer: d)
Time taken by pipes R and E together to fill the tank = N = 1/[(1/3.2) – (1/4)]
N = 16 hours
Let time after which pipe A should stop working = ‘T’ hours
According to the question:
T * [(1/5) – (1/15) – (1/10)] + (16 – T) * [(1/5) – (1/10)] = 1
(T/30) + 3(16 – T)/30 = 1
T + 48 – 3T = 30
2T = 48 – 30
T = 9 hours
5) Answer: c)
Part of tank fill by pipes R, S and D together is 40 minutes
= (40/60) * [(1/3.2) + (1/2.4) – (1/6)] = 3/8
Remaining part of the tank = 1 – (3/8) = 5/8
Part of tank filled by pipes R, C and D together in 1 hour
= (1/3.2) – (1/12) – (1/6) = 1/16
Required time taken to fill the remaining part of the tank = (5/8) ÷ (1/16)
= 10 hours
6) Answer: a)
The ratio of ages of Ram, Sunil and Shon is,
Ram: Sunil: Shon=3:4:2
The product of the ages of Shon and Sunil is,
4x * 2x=648
X=9 years
Shon’s age=2 * 9=18 years
Sunil’s age=4 * 9=36 years
Ram’s age=3 * 9=27 years
The product of the ages of Sunil and Rahul is 864 years. So,
Rahul’s age=864/36=24 years
The ratio of the ages of Rahul to Surya is 4:3, then
Surya’s age= (3/4) * 24= 18 years
The sum of the ages of Shon and Nitish is 30 years. So,
Nitish’s age=30 – 12=18 years
We can find answers of all the given questions.
7) Answer: a)
Circumference of the circle is 44 cm.
44=2 * (22/7) * r
Radius of the circle=7 cm
The ratio of the radius of the circle to the cylinder is 1:2. So,
Radius of the cylinder=(2/1)* 7=14 cm
The height of the cylinder is 10 cm more than that of the radius of the cylinder. So,
Height of the cylinder=14 + 10=24 cm
Volume of the cylinder=πr2 h
(22/7) * 14 * 14 * 24=14784 cm3
TSA of the cylinder=2πr (h + r)
2 * (22/7) * 7(7 + 24)=1364 cm2
Radius of the cone= Radius of the circle = 7 cm
Height of the cone=Height of the cylinder=24 cm
Length of the cone=√ (242 + 72) = 25 cm
CSA of the cone=πrl
22/7 * 7 * 25=550 cm2
We can find answers of all the given questions.
8) Answer: e)
Profit ratio of A, B ,C=(x * 4 + 2x * 8):((x + 2000) * 12):(x – 1000) *8
20x:(12x + 24000):(8x – 8000)
The profit share of France is Rs.5000 and the total profit is Rs.12000. So,
20x/(40x + 16000)=5000/12000
200x + 80000=240x
40x=80000
X=2000
Profit ratio of A, B ,C=40000:48000:8000=5:6:1
Sam’s profit share=1/12 * 12000=1000
Initial investment of Sam=2000 – 1000=1000
Prince’s profit share=6/12 * 12000=6000
Interest rate not given. So we can’t find the interest received by prince after 5 years.
We can find the answers of A, B and D questions only.
9) Answer: c)
The ratio of the speed of the stream to boat is 2:3.
Speed of the boat=3x
Speed of stream=2x
Downstream speed=3x + 2x=5x
Upstream speed=3x – 2x=x
From option (A)
(40/5x) + (40/x) =8
48=8x
x=6
Speed of stream=2 * 6=12 kmph
This will not satisfy the given condition.
From option (B)
(50/5x) + (50/x) =10
60=10x
x=6
Speed of stream=2 * 6=12 kmph
This will not satisfy the given condition.
From option (C)
(60/5x) + (60/x) =12
72=12x
x=6
Speed of stream=2 * 6=12 kmph
This will satisfy the given conditions.
From option (D)
(70/5x) + (70/x) =14
84=14x
x=6
Speed of stream=2 * 6=12 kmph
This will not satisfy the given condition.
10) Answer: d)
1st mixture ratio=4:3(here it is the mixture after sold)
2nd mixture ratio=30:15=2:1
Final mixture ratio=3:5
Then the ratio of the mixture of (1) and (2) is,
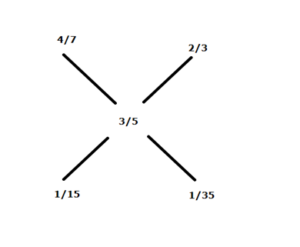
=7:3
After sold the mixture and then the quantity of the mixture=(7/3)* (30+15)=105 liters
From option (A)
If Sold mixture=15 liters.
Volume of the initial mixture=105 + 15=120 liters
This will satisfy the given condition.
From option (B)
If Sold mixture=10 liters
Initial volume of the mixture=10 + 105=115 liters
This will not satisfy the given condition.
From option (C)
If Sold mixture=20 liters.
Volume of the initial mixture=105 + 20=125 liters
This will not satisfy the given condition.
From option (D)
If Sold mixture=25 liters.
Volume of the initial mixture=105 + 25=130 liters
This will satisfy the given condition.





