SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 4654]Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1- 5): Study the following information carefully and answer the given questions.
The bank offers four different schemes
Scheme A: Gives a return of 10% p.a. interest being compounded annually
Scheme B: Gives a return of 10% p.a. interest being compounded half-yearly
Scheme C: Gives a return of 20% p.a. compounded annually but 10% of the amount at the end of each year is paid as administrative charges and remaining 90% is reinvested (or) received.
Scheme D: Gives a return of 30 % p.a. simple interest but 20% of the amount at the end of each year is paid as administrative charges and remaining 80% is reinvested (or) received.
The bar graph shows the total amount (in lakhs) they had initially.
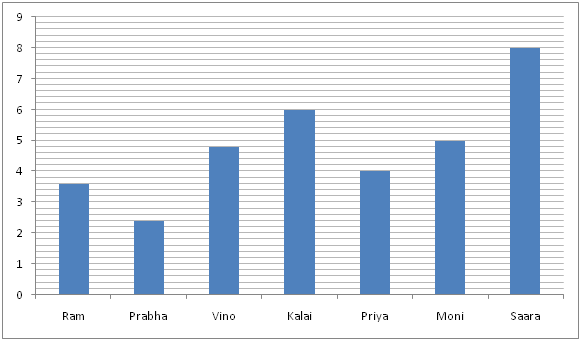
1) Ram invested 20% of the amount in scheme C, 40% of the remaining amount in scheme D and the remaining amount in scheme A for two years. He started a business with Rs. 8834.56 less than the 50% of the total amount what he received at the end of two years in all the schemes together. After 5 months, Prabha joins with him with 60% of the amount he had initially. Find the profit ratio of Ram and Prabha at the end of one year?
a) 49: 27
b) 53: 49
c) 12: 29
d) 50: 21
e) None of these
2) Quantity I: Vino invested two fifth of the amount in scheme B, 40% of the remaining amount invested in scheme D and the remaining amount invested in scheme A. Find the 50% of the interest received by her at the end of one year.
Quantity II: Kalai invested equal amount in scheme C and D for two years. Find the total interest received by her.
Quantity III: Priya invested total amount in scheme D for one year. Again she invested the amount what she received at the end of one year in scheme A. Find the total amount she received at the end of two years
Which of the following should be placed in the blank spaces of the expression “Quantity I__ Quantity II___Quantity III” from left to right with respect to the above statements?
a) >, >
b) >, <
c) <, >
d) <, <
e) None of these
3) Prabha invested total amount in scheme D for first year, in scheme C for second year, in scheme A for third year and in scheme B for fourth year. In the same way, Saara invested X% of the amount she had initially, find the difference between the total amount received at the end of fourth year by Prabha to that of Saara?
Statement I: If Saara invested (x+20) % of the amount in scheme B for one year, then she would be able to receive total amount of Rs. 529200.
Statement II: Saara invested same amount and got Rs.8000 more interest than Prabha. Prabha invested his total amount in scheme A for one year.
a) Statement I alone is sufficient to answer the question
b) Statement II alone is sufficient to answer the question
c) Either statement I or II alone is sufficient to answer the question
d) Both the statements are not necessary to answer the question
e) Both the statements are necessary together to answer the question
4) Moni invested half of the amount in scheme A for one year and the remaining amount invested in Scheme C for one year. Which of the following option is not true according to the given information?
a) Total interest received by Moni in both the schemes together is Rs. 45000
b) Total interest received in scheme A is Rs. 5000 less than in scheme C
c) 28% of the total interest received in scheme C is Rs. 5600
d) Difference between the 42% of total amount received in scheme C and 29% of total amount received in scheme A is Rs. 47700
e) All the above options are true
5) Prabha, Vino, Kalai, Priya, Moni and Saara invested 100%, 50%, 40%, 60%, 48%, 30% respectively in scheme C. Who among the following got maximum interest at the end of three years?
a) All of them got equal interest
b) Moni and Priya
c) Prabha and Vino
d) Kalai and Saara
e) None of these
Directions (6 – 10): Each question below contains a statement followed by Quantity I and Quantity II. Find both to find the relationship among them. Mark your answer accordingly.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II (or) relationship cannot be determined
6) Quantity I: Difference between compound interest and simple interest on a certain sum at 5 % per annum after two years is Rs. 100. Find the compound interest on that sum at 8 % per annum after three years.
Quantity II: Compound interest on a certain sum at 6 % per annum after two years is Rs. 5562. Find the simple interest on that sum at 10 % per annum after 5 years.
7) Quantity I: A bag contains 2 green, 3 black and some white balls. Probability of drawing 1 green ball from the bag is 1/5. Find the probability of drawing three balls of different colour.
Quantity II: A bag contains 3 green, 4 red and 5 blue balls. Find the probability of drawing 3 balls of same colour.
8) Quantity I: Uma, Bubun and Sanju entered into a partnership with investment in the ratio 6:7:5 respectively. After one year, Uma made her investment 1.5 times and Sanju doubled her investment. At the end of two years, they earned a total profit of Rs. 132000. Find the share of Uma in the profit.
Quantity II: Nimi, Kiran and Seema entered into a partnership with investment in the ratio 4:2:3. After one year, Kiran doubled her investment. After one more year, Seema doubled her investment. At the end of three years, they earned a total profit of Rs.102000. Find the share of Nimi in the profit.
9) Quantity I: Find the value of x : 46 x 54 ÷ 26 x 15 = 75 x 53 x 8x
Quantity II: Find the value of y: 104 x 42 ÷ 28 = (25)2 x 4y
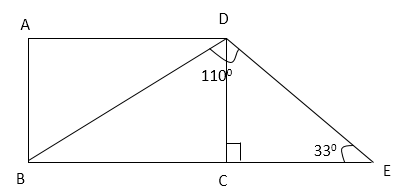
10) Quantity I: Find the value of ∠OBC

Quantity II: Find the value of ∠DBC.
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Answers :
1) Answer: d)
Total amount Ram had initially = Rs. 360000
In scheme C:
20% of the total amount in scheme C = 360000 * 20/100
= 72000
Total amount received at the end of 1st year including administrative charge
= 72000 * (120/100)
= 86400
Administration charge after 1st year = 86400 * 10/100 = 8640
Remaining amount invested after 1st year = (86400 – 8640) =77760
Total amount received at the end of 2nd year including administrative charge
= 77760 * (120/100) = 93312
Total amount received at the end of 2nd year excludes administrative charge
= 93312 * 90/100 = 83980.8
Total interest received at the end of two years = 83980.8 – 72000
= Rs.11980.8
In scheme D:
40% of the remaining amount in scheme D = (360000-72000)*40/100
= 115200
Total amount received at the end of 1st year = 115200 * 130/100
= 149760
Remaining amount invested after 1st year = 149760 * 80/100
= 119808
Total amount received at the end of 2nd year including administrative charge
= 119808 * 130/100
= 155750.4
Total amount received at the end of 2nd year excludes administrative charge
= 155750.4 * 80/100
= 124600.32
Total interest received at the end of two years = 124600.32 – 115200
= 9400.32
In scheme A:
Remaining amount in scheme A = 360000 – (72000 + 115200)
= 172800
Total amount received at the end of two years
= 172800 * (1+10/100)2
= 172800 * (11/10)2
= 209088
Total interest received at the end of two years = 209088 – 172800
= Rs. 36288
Total interest received at the end of two years in all the schemes together
= Rs.11980.8 + 9400.32 + 36288
= Rs.57669.12
Total amount received by Ram at the end of two years = 360000 + 57669.12
= Rs. 417669.12
Total amount received by Ram is
= 417669.12 * 50/100 – 8834.56
= 208834.56 – 8834.56
= 200000
60% of the amount invested by Prabha = 60/100 * (240000)
= 144000
Profit ratio of Ram and Prabha
= (200000*12): (144000*7)
= 2400000:1008000
= 50: 21
2) Answer: d)
Quantity I: Vino invested two fifth of the amount in scheme B, 40% of the remaining amount invested in scheme D and the remaining amount invested in scheme A. Find the 50% of the interest received by her at the end of one year.
Two-fifth of the amount invested in scheme B = 480000 * 2/5
= 192000
Total amount received by Vino at the end of one year = 192000 * (1+5/100)2
= 192000 * (21/20)2
= 192000 * 441/400
= 211680
Total interest received by Vino at the end of one year in scheme B
= 2111680 – 192000
= Rs. 19680
40% of the remaining amount invested in scheme D
= (480000 – 192000) * 40/100
= 115200
Total amount received by Vino at the end of one year in scheme D including administrative charge
= 115200 * 130/100
= 149760
Total amount received by Vino at the end of one year in scheme D excluding administrative charge
= 149760 * 80/100
= 119808
Total interest received by Vino at the end of one year in scheme D
= 119808 – 115200
= Rs. 4608
Remaining amount invested by Vino in scheme A = (480000 – 192000 – 115200)
= 172800
Total amount received by Vino in scheme A at the end of one year
= 172800 * 110/100
= 190080
Total interest received by Vino in scheme A at the end of one year
= 190080 – 172800
= Rs. 17280
Total interest received by Vino at the end of one year all the schemes together is
= 19680 + 4608 + 17280
= Rs. 41568
Required amount = 50/100 * 41568
= Rs. 20784
Quantity II: Kalai invested equal amount in scheme C and D for one year. Find the total interest received by her.
Total amount kalai had initially = 600000
Total amount received by Kalai at the end of one year in scheme C including administrative charge
= 300000 * (120/100)
= 360000
Total interest received by Kalai = (360000 * 90/100) – 300000
= 324000 – 300000
= Rs. 24000
Total amount received by Kalai at the end of one year in scheme D including administrative charge
= 300000 * (130/100)
= 390000
Total interest received by Kalai = (390000*80/100) – 300000
= 312000 – 300000
= Rs. 12000
Total interest received by Kalai in scheme C and D together = 24000 + 12000
= Rs. 36000
Quantity III: Priya invested total amount in scheme D for one year. Again she invested the amount what she received at the end of one year in scheme A. Find the total amount she received at the end of two years
Total amount Priya had initially = 400000
Total amount received by Priya at the end of 1st year in scheme D including administrative charges
= 400000 * (130/100)
= 520000
Total amount invested in Scheme A = 520000 * 80/100
= 416000
Total amount received by Priya at the end of 2nd year in scheme A
= 416000 * 110/100
= 457600
Total interest received by Priya at the end of two years in both the schemes together
= 457600 – 400000
= Rs. 57600
Quantity I < Quantity II < Quantity III
3) Answer: c)
Total amount Prabha had initially Rs. 240000
First year,
Total amount = 240000 * 130/100 = 312000
Reinvestment amount after 1st year = 312000 * 80/100
= 249600
Second year,
Total amount = 249600 * 120/100
= 299520
Reinvestment amount after 2nd year = 299520 * 90/100
= 269568
Third year,
Total amount = 269568 * (110/100)
= 296524.8
Fourth year,
Total amount = 296524.8 * (105/100)2
= 326918.592
We need to find Saara’s investment amount, then only we can find the difference between the total amounts received by Prabha to that of Saara after 4 years
From statement I: If Saara invested (x + 20) % of the amount in scheme B for one year, then she would be able to receive total amount of Rs. 529200.
Total amount for one year in scheme B = P*(1+(R/2)/100)2n
529200 = P *(1 + 5/100)2
529200 = P * (21/20)2
P =529200 * (20/21)2
P = 529200 * (20/21)*(20/21)
P = 480000
Saara invested percentage of amount = (480000/800000) * 100
= 60%
(x+20)% = 60%
= > x = 40%
From statement I, we could find the investment amount of Saara. Then, we proceed in the same way to find the amount as we calculated for Prabha. Now we could find the difference between the total amounts received by Prabha at the end of four years to that of Saara.
Hence, statement I alone is sufficient to answer the question.
From statement II: Saara invested same amount and got Rs. 8000 more interest than Prabha. Prabha invested his total amount in scheme A for one year.
Interest received by Prabha at the end of one year in scheme A
= [240000 * 110/100] – 240000
= 264000 – 240000
= Rs.24000
Saara’s interest at the end of one year in scheme A = 24000 + 8000
= 32000
32000 = P *(1+10/100)1 – P
32000 = P * [(110/100) – 1]
32000 = P*10/100
= > P = 32000*(100/10)
= Rs. 320000
From statement II, we could find the investment amount of Saara. Then, we proceed in the same way to find the amount as we calculated for Prabha. Now we could find the difference between total amounts received by Prabha at the end of four years to that of Saara.
Hence, statement II alone is sufficient to answer the question.
4) Answer: e)
In scheme A,
Total amount had Moni initially = Rs. 500000
Half of the amount = 250000
Total amount received by Moni at the end of one year in scheme A
= 250000 * 110/100
= 275000
Total interest received by Moni in scheme A = 275000 – 250000
= Rs. 25000
Total amount received by Moni at the end of one year in scheme C (Including administrative charges)
= 250000 * 120/100
= 300000
Total amount received by Moni at the end of one year in scheme C (Excluding administrative charges)
= 300000 * 90/100
= 270000
Total interest received by Moni in scheme C = 270000 – 250000
= Rs. 20000
5) Answer: a)
Prabha’s 100% of the amount = 240000*100/100 = 240000
Vino’s 50% of the amount = 480000*50/100 = 240000
Kalai’s 60% of the amount = 600000 * 40/100 = 240000
Priya’s 40% of the amount = 400000*60/100 = 240000
Moni’s 48% of the amount = 500000*48/100 = 240000
Saara’s 30% of the amount = 800000*30/100 = 240000
All of them invested same amount in scheme C, so they will get equal interest at the end of three years.
Direction (6-10) :
6) Answer: b)
Quantity I: Difference between compound interest and simple interest on a certain sum at 5% per annum after two years is Rs.100. Find the compound interest on that sum at 8% per annum after three years.
We know that,
CI – SI = P x (r/100)2
=> 100 = P x (5/100)2
=> 100 = P x (1/20)2
=> 100 = P x 1/400
=> P = Rs. 40000
We know that
CI = P x (1 + r/100)t – P
= 40000 x (1 + 8/100)3 – 40000
= 40000 x 108/100 x 108/100 x 108/100 – 40000
= 50388.48 – 40000
= Rs. 10388.48
Quantity II: Compound interest on a certain sum at 6% per annum after two years is Rs. 5562. Find the simple interest on that sum at 10% per annum after 5 years.
We know that
CI = P x (1 + r/100)t – P
=> 5562 = P x (1 + 6/100)2 – P
=> 5562 = P x 106/100 x 106/100 – P
=> 5562 = P x 53/50 x 53/50 – P
=> 5562 = 2809P/2500 – P
=> 5562 = (2809 – 2500)/2500 x P
=> 5562 = 309/2500 x P
=> 5562 x 2500/309 = P
=> P = Rs. 45000
SI = (P x r x t)/100
= (45000 x 10 x 5)/100
= Rs. 22500
Hence, Quantity I < Quantity II
7) Answer: a)
Quantity I: A bag contains 2 green, 3 black and some white balls. Probability of drawing 1 green ball from the bag is 1/5. Find the probability of drawing three balls of different colour.
Green = 2
Black = 3
Let, white = n
Total number of balls = 2 + 3 + n = 5 + n
2/(5 + n) = 1/5
=> 10 = 5 + n
=> n = 10 – 5
=> n = 5
Total number of balls in the bag = 5 + 5 = 10
Required probability = (2c1 x 3c1 x 5c1)/10c3
= (2 x 3 x 5)/120= ¼
Quantity II: A bag contains 3 green, 4 red and 5 blue balls. Find the probability of drawing 3 balls of same colour.
Required probability = (3c3 + 4c3 + 5c3)/12c3
= (1 + 4 + 10)/220
= 15/220
= 3/44
Hence, Quantity I > Quantity II
8) Answer: a)
Quantity I: Uma, Bubun and Sanju entered into a partnership with investment in the ratio 6:7:5 respectively. After one year, Uma made her investment 1.5 times and Sanju doubled her investment. At the end of two years, they earned a total profit of Rs.132000. Find the share of Uma in the profit.
Let, amount invested by Uma, Bubun and Sanju be Rs.6k, Rs.7k and Rs.5k respectively.
Ratio of share in the profit:
Uma : Bubun : Sanju = (6k + 6k*1.5) : (7k x 2) : (5k + 5k*2)
= 15k : 14k : 15k
= 15:14:15
Share of Uma in the profit = [15/(15 + 14 + 15)] x 132000
= (15/44) x 132000 = Rs. 45000
Quantity II: Nimi, Kiran and Seema entered into a partnership with investment in the ratio 4:2:3. After one year, Kiran doubled her investment. After one more year, Seema doubled her investment. At the end of three years, they earned a total profit of Rs. 102000. Find the share of Nimi in the profit.
Let, the amount invested by Nimi, Kiran and Seema be Rs.4k, Rs.2k and Rs.3k respectively.
Ratio of share in the profit:
Nimi : Kiran : Seema = (4k x 3) : (2k + 4k x 2) : (3k x 2 + 6k)
= 12k : 10k : 12k
= 6 : 5 : 6
Share of Nimi in the profit = [6/(6 + 5 + 6)] x 102000
= (6/17) x 102000
= 6 x 6000
= Rs. 36000
Hence, Quantity I > Quantity II
9) Answer: a)
Quantity I: Find the value of x : 46 x 54 ÷ 26 x 15 = 75 x 53 x 8x
(22)6 x 54 ÷ 26 = 5 x 53 x (23)x
=> (2)(12 – 6)= (2)3x
=> 6 = 3x
=> x = 2
Quantity II: Find the value of y: 104 x 42 ÷ 28 = (25)2 x 4y
54 x 24 x (22)2 ÷ 28 = (52)2 x (22)y
=> 54 x 2(4 + 4 – 8) = 54 x 22y
=> 20 = 22y
=> 2y = 0
=> y = 0
Hence, Quantity I > Quantity II
10) Answer: b)
Quantity I:
Find the value of ∠OBC.

∠ACB = ½ x 1020 [Angle subtended by an arc at the centre is double the angle subtended by the arc at any point on the circle.]
=>∠ACB = 510
Reflex ∠AOB = 3600 – 1020 = 2580
∠OBC = 3600 – 270 – 2580 – 510 [Angle sum property of a quadrilateral]
=>∠OBC = 240
Quantity II: Find the value of ∠DBC.

∠CDE = 1800 – 900 – 330 [Angle sum property of a triangle]
=>∠CDE = 570
Now, ∠CDB = 1100 – 570 = 530
∠DBC = 1800 – 900 – 530 [Angle sum property of a triangle]
=>∠DBC = 1800 – 1430
=>∠DBC = 570
Hence, Quantity I < Quantity II
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| IBPS SO/NIACL AO Prelims – Reasoning | 10.00 AM |
| IBPS SO/NIACL AO Prelims – Reasoning (Hindi) | 10.30 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude | 11.00 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude (Hindi) | 11.30 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| IBPS SO/NIACL AO Prelims – English Language | 1.00 PM |
| SSC Practice Questions (Reasoning/Quantitative aptitude) | 2.00 PM |
| IBPS Clerk – GK Questions | 3.00 PM |
| SSC Practice Questions (English/General Knowledge) | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| SBI PO/IBPS Clerk Mains – Reasoning | 6.00 PM |
| SBI PO/IBPS Clerk Mains – Quantitative Aptitude | 7.00 PM |
| SBI PO/IBPS Clerk Mains – English Language | 8.00 PM |





