Dear Aspirants, the most awaited notification of SBI PO – 2019 has been released. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 6648]
Click Here to Take Free Mock Test For SBI PO Mains
Direction (1 – 5): Study the following data carefully and answer the questions:
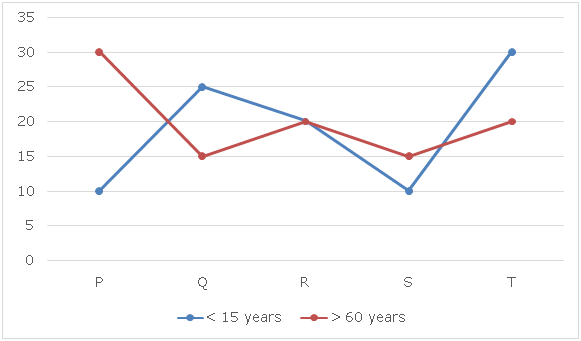
There are total five countries P, Q, R, S and T whose employment rate is to be calculated.
Formulas for calculating Unemployment rate is given below:
Unemployment Rate= Unemployed/(Labour Force)*100
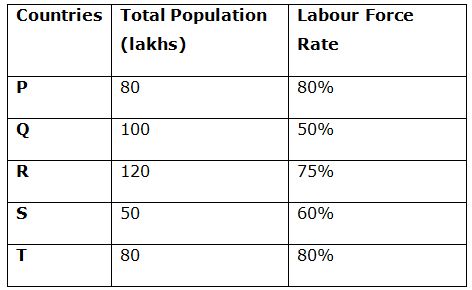
Labour Force Rate= (Person willing to Work (Labour Force))/(Total Population (15-60 years))*100
Line graph given below shows the population (lakhs) of those five countries of 3 different age groups such as: less than 15 years, more than 60 years of age.
- Labour force is calculated from the population of age group (15 – 60) years and employment and unemployment rate is calculated from the Labour Force only.
Table given shows the labour force rate and total population of those five states.
1) If out of total population of country P, 30% are actually employed, then what is the per cent of unemployment in that country?
a) 25%
b) 20%
c) 30%
d) 40%
e) None of these
2) If unemployment rate of country Q is 40%, then what is the ratio of employed population to the population of age greater than 60 years of that country?
a) 3: 2
b) 4: 3
c) 6: 5
d) 5: 4
e) None of these
3) If unemployment rate of country P, Q and R is ‘x’%, ‘x + 25’% and 60% respectively and unemployed population in countries P is 15200 less than that in country R, then what is the unemployed population (thousand) in country Q?
a) 27
b) 24
c) 19.5
d) 20.4
e) None of these
4) If unemployment rate of country R is 15 more than that of country S and ratio of unemployed population of countries R to that of S is 5: 1, than that in country S, then what is the sum of unemployed population (thousands) in both the countries together?
a) 45
b) 54
c) 36
d) 60
e) None of these
5) If unemployed population in country T is ‘x’% of total population of age group (< 15) and ‘x + 18’% of total population of age group (> 60), then what is the unemployment rate of country T?
a) 55%
b) 45%
c) 65%
d) 75%
e) None of these
Direction (6 – 10): Study the following data carefully and answer the questions:
There are total five players A, B, C, D and E in the game of cricket who can do either bat or ball perfectly and they can also do other thing part time. Their points in the rank table is decided by the numbers of runs scored and number of wickets taken.
Formula to calculate points earned by player while batting and points earned by a player while bowling is given below:
Points of a batsman = 50% of number of runs scored – 20% of total balls faced.
Points of a bowler = 20 * number of wickets taken – Numbers of balls bowled
It is also given that, while calculating overall points of a pure batsman points earned while bowling has more weightage as bowling is not his expertise area and vice versa. So, formula to calculate overall points is also given below:
Overall points of a pure batsman = Points while bating + 2 * Points while bowling
Overall points of a pure bowler = 2 * Points while bating + Points while bowling
Strike rate of batsman = (Runs scored/Ball faced) * 100
Strike rate of bowler = Ball bowled/Wickets taken
* Note: If in any case the points go negative, then it will consider as zero.
6) Sachin is batsman Zaheer is bowler, if in a match Sachin scored 120 runs at strike rate of 75 and he didn’t bowl while Zaheer took 4 wickets with strike rate of 10 and he didn’t bat, then what is the difference between total points of Sachin and Zaheer in that match?
a) 32
b) 12
c) 28
d) 24
e) None of these
7) If Irfan is a pure bowler and, in a match, he scored 60 runs with strike rate of 50 and he also took 2 wickets at strike rate of 15, then what is the total points earned by Irfan in that match?
a) 22
b) 26
c) 32
d) 36
e) None of these
8) If Smith is a pure batsman but, in a match, he scored some runs at strike rate of 80 and also, he took 1 wicket with strike rate of 15 and total points earned by him in that match is 22 points, then what is the total runs scored by him in that match?
a) 72
b) 36
c) 60
d) 48
e) None of these
9) If Stokes a pure bowler and, in a match, he took 3 wickets at ‘x’ strike rate and also scored 24 runs with strike rate of 50 and total points earned by Stokes in that match is 16.8, then what is the value of ‘x’?
a) 24
b) 16
c) 30
d) 18
e) None of these
10) Kohli and Root are pure batsman, in a match, Kohli scored 32 runs with strike rate of 160 and Root scored 28 runs with strike rate of 140. If Kohli and Roots together took 3 wickets with strike rate of 18 and 15 runs respectively. If total points earned both the players in that match is same, then what is the total wickets taken by Kohli in that match?
a) 0
b) 1
c) 2
d) 3
e) None of these
Answers :
Direction (1-5) :
1) Answer: a)
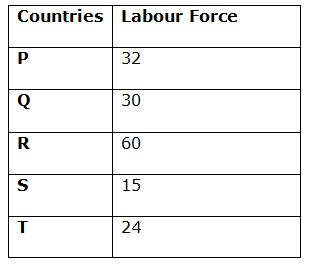
Population of age group (15 – 60) in country P = 80 – (10 + 30) = 40
80% = (Labour Force/40) * 100
Labour Force in country P = (80/100) * 40 = 32
Population of age group (15 – 60) in country Q = 100 – (15 + 25) = 60
50% = (Labour Force/60) * 100
Labour Force in country Q = (50/100) * 60 = 30
Population of age group (15 – 60) in country R = 120 – (20 + 20) = 80
75% = (Labour Force/80) * 100
Labour Force in country R = (75/100) * 80 = 60
Population of age group (15 – 60) in country S = 50 – (10 + 15) = 25
60% = (Labour Force/25) * 100
Labour Force in country S = (60/100) * 25 = 15
Population of age group (15 – 60) in country T = 80 – (20 + 30) = 30
80% = (Labour Force/50) * 100
Labour Force in country T = (80/100) * 30 = 24
Total population of country P = 80
Total employed in country P = 30% of 80 = 24
Total unemployed out of Labour Force = 30 – 24 = 8
Unemployment rate = (8/32) * 100 = 25%
2) Answer: c)
Population of age group (15 – 60) in country P = 80 – (10 + 30) = 40
80% = (Labour Force/40) * 100
Labour Force in country P = (80/100) * 40 = 32
Population of age group (15 – 60) in country Q = 100 – (15 + 25) = 60
50% = (Labour Force/60) * 100
Labour Force in country Q = (50/100) * 60 = 30
Population of age group (15 – 60) in country R = 120 – (20 + 20) = 80
75% = (Labour Force/80) * 100
Labour Force in country R = (75/100) * 80 = 60
Population of age group (15 – 60) in country S = 50 – (10 + 15) = 25
60% = (Labour Force/25) * 100
Labour Force in country S = (60/100) * 25 = 15
Population of age group (15 – 60) in country T = 80 – (20 + 30) = 30
80% = (Labour Force/50) * 100
Labour Force in country T = (80/100) * 30 = 24

Unemployment rate = (Unemployed/Labour Force) * 100
40 = (Unemployed/30) * 100
Unemployed = 12
Employed = 30 – 12 = 18
Required ratio = 18: 15 = 6: 5
3) Answer: a)
Population of age group (15 – 60) in country P = 80 – (10 + 30) = 40
80% = (Labour Force/40) * 100
Labour Force in country P = (80/100) * 40 = 32
Population of age group (15 – 60) in country Q = 100 – (15 + 25) = 60
50% = (Labour Force/60) * 100
Labour Force in country Q = (50/100) * 60 = 30
Population of age group (15 – 60) in country R = 120 – (20 + 20) = 80
75% = (Labour Force/80) * 100
Labour Force in country R = (75/100) * 80 = 60
Population of age group (15 – 60) in country S = 50 – (10 + 15) = 25
60% = (Labour Force/25) * 100
Labour Force in country S = (60/100) * 25 = 15
Population of age group (15 – 60) in country T = 80 – (20 + 30) = 30
80% = (Labour Force/50) * 100
Labour Force in country T = (80/100) * 30 = 24

Unemployment rate of P = (Unemployed/Labour Force) * 100
x = (Unemployed/32) * 100
Unemployed in P = 0.32x
Unemployment rate of R = (Unemployed/Labour Force) * 100
60 = (Unemployed/60) * 100
Unemployed in R = 36
According to the question:
36 – 0.32x = 15200/1000
0.32x = 20.8
x = 65
Now,
Unemployment rate in Q = (Unemployed/Labour Force) * 100
(x + 25) = (Unemployed/30) * 100
Unemployed in Q = [(65 + 25) * 30]/100
Unemployed in Q = 27
4) Answer: b)
Population of age group (15 – 60) in country P = 80 – (10 + 30) = 40
80% = (Labour Force/40) * 100
Labour Force in country P = (80/100) * 40 = 32
Population of age group (15 – 60) in country Q = 100 – (15 + 25) = 60
50% = (Labour Force/60) * 100
Labour Force in country Q = (50/100) * 60 = 30
Population of age group (15 – 60) in country R = 120 – (20 + 20) = 80
75% = (Labour Force/80) * 100
Labour Force in country R = (75/100) * 80 = 60
Population of age group (15 – 60) in country S = 50 – (10 + 15) = 25
60% = (Labour Force/25) * 100
Labour Force in country S = (60/100) * 25 = 15
Population of age group (15 – 60) in country T = 80 – (20 + 30) = 30
80% = (Labour Force/50) * 100
Labour Force in country T = (80/100) * 30 = 24

Let unemployed population of country R and S is ‘5x’ and ‘x’ respectively.
Unemployment rate of R = (Unemployed/Labour Force) * 100
Unemployment rate of R = (5x/60) * 100
Unemployment rate of R = 25x/3
Unemployment rate of S = (Unemployed/Labour Force) * 100
Unemployment rate of S = (x/15) * 100
Unemployment rate of S = 20x/3
According to the question:
(25x/3) – (20x/3) = 15
x = 9
Sum of unemployed population (thousands) in both the countries together = 5x + x = 6x = 54
5) Answer: b)
Population of age group (15 – 60) in country P = 80 – (10 + 30) = 40
80% = (Labour Force/40) * 100
Labour Force in country P = (80/100) * 40 = 32
Population of age group (15 – 60) in country Q = 100 – (15 + 25) = 60
50% = (Labour Force/60) * 100
Labour Force in country Q = (50/100) * 60 = 30
Population of age group (15 – 60) in country R = 120 – (20 + 20) = 80
75% = (Labour Force/80) * 100
Labour Force in country R = (75/100) * 80 = 60
Population of age group (15 – 60) in country S = 50 – (10 + 15) = 25
60% = (Labour Force/25) * 100
Labour Force in country S = (60/100) * 25 = 15
Population of age group (15 – 60) in country T = 80 – (20 + 30) = 30
80% = (Labour Force/50) * 100
Labour Force in country T = (80/100) * 30 = 24

Let unemployed population in T = ‘a’
Total population of age group (< 15) in T = 30
a = x% of 30
a = 0.3x ……… (1)
Total population of age group (< 15) in T = 30
a = (x + 18)% of 20
From equation (1):
0.3x = 0.2(x + 18)
0.3x = 0.2x + 3.6
x = 36
Unemployment rate = (a/24) * 100
= (0.3x/24) * 100
= 45%
Direction (6-10) :
6) Answer: b)
Balls faced by Sachin = (120/75) * 100 = 160
Balls bowled by Zaheer = 10 * 4 = 40
Total points of Sachin = 50% of 120 – 20% of 160 = 60 – 32 = 28
Total points of Zaheer = 20 * 4 – 40 = 40
Required difference = 40 – 28 = 12
7) Answer: a)
Number of balls faced by Irfan = (60/50) * 100 = 120
Number of balls bowled by Irfan = 2 * 15 = 30
Points earned while batting = 50% of 60 –20% of 120 = 30 – 24 = 6
Points earned while bowling = 20 * 2 – 30 = 40 – 30 = 10
Hence, total points earned by Irfan= 2 * 6 + 10 = 22
8) Answer: d)
Let runs scored by Smith = ‘x’
Balls faced by Smith = (x/80) * 100 = 1.25x
Balls bowled by Smith = 1 * 15 = 15
Points earned while batting = 50% of x – 20% of 1.25x = 0.25x
Points earned while bowling = 20 * 1 – 15 = 5
Total points earned by Smith = 0.25x + 2 * 5 = 22
0.25x = 12
x = 48
Hence, runs scored by Smith = x = 48
9) Answer: b)
Total balls bowled by Stokes = 3 * x = 3x
Total balls faced by Stokes = (24/50) * 100 = 48
Points earned while batting = 50% of 24 – 20% of 48 = 2.4
Points earned while bowling = 20 * 3 – 3x = (60 – 3x)
Total points earned = (60 – 3x) + 2 * 2.4 = 16.8
3x = 48
x = 16
10) Answer: c)
Let total wicket taken by Kohli and Root in that match is ‘x’ and ‘3 – x’ respectively.
Kohli:
Total ball faced = (32/160) * 100 = 20
Total balls bowled = 18 * x = 18x
Points earned while batting = 50% of 32 – 20% of 20 = 16 – 4 = 12
Points earned while bowling = 20 * x – 18x = 2x
Root:
Total ball faced = (28/140) * 100 = 20
Total balls bowled = 15 * (3 – x)
Points earned while batting = 50% of 28 – 20% of 20 = 14 – 4 = 10
Points earned while bowling = 20 * (3 – x) – 15 * (3 – x) = (15 – 5x)
According to the question:
12 + 2 * 2x = 10 + 2 * (15 – 5x)
12 + 4x = 10 + 30 – 10x
14x = 28
x = 2
Hence, total wickets taken by Kohli = x = 2





