SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 4777]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1-5): Read the following passage carefully and answer the given questions.
Rahul has five different bags P, Q, R, S and T which contains four different colour caps viz. black, pink, red and green.
Bag P: Number of pink colour caps is 15 which is 150% of the number of green colour caps. Number of black colour caps is 80% of pink colour caps. One cap is taken and the probability of getting a pink colour cap is 1/3.
Bag Q: The ratio of the number of black colour caps to the pink is 5: 6. The ratio of the number of pink colour caps to red is 4: 5. The ratio of the number of red colour caps to green is 3: 1. Two caps are taken and the probability of getting pink and one red colour caps is 120/581.
Bag R: Total number of caps is 35 more than the total number of caps in bag P. Total number of pink and red colour caps is 50% of the total number of caps. Number of pink colour cap is 150 percentage of the number of red colour caps. The number of green colour caps is 60% of the number of black colour caps.
Bag S: Number of pink colour caps is equal to the number of red colour caps and 5 caps less than the number of green colour caps. Total number of caps in the bag is 5 more than bag P. One cap is taken and the probability of getting a black colour cap is 3/10.
Bag T: Total number of caps in the bag is 66 (2/3)% of the total number of caps in the bag P. Number of black colour caps is one-sixth of the total number of caps and is equal to the number of red colour caps. One ball is taken and the probability of getting a green colour caps is 1/3.
1) Quantity I: Two caps taken randomly from the bag S. What is the probability of getting one red and one pink?
Quantity II: Two caps taken randomly from the bag T. What is the probability of getting both are pink colour?
Quantity III: 7/20
Note: The options represent the relations of Quantity I __ Quantity II __ Quantity III
A) >
B) <
C) =
D) ≤
E) ≥
a) B, C
b) C, D
c) B, B
d) A, B
e) None of these
2) Quantity I: One cap is taken randomly from bag R, S and T. What is the probability of getting a black colour cap?
Quantity II: Two caps taken randomly from bag P. What is the probability of getting at least one green cap?
a) Quantity I > Quantity II
b) Quantity II > Quantity I
c) Quantity I ≥ Quantity II
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II (or) Relationships cannot be determined
3) In bag Q, 25% of caps sold at 20% discount in which 33(1/3) % is red colour caps. Two caps taken without replacement, what is the probability of getting one red colour cap without discount and another cap with discount?
a) 21/332
b) 23/332
c) 19/332
d) 17/332
e) None of these
4) If x green caps taken out from bag S and added to bag T, in the same way 2x red colour caps and x pink colour caps taken out from bag T and added to bag S. One cap is taken from bag S and the probability of getting black colour cap is 1/6. Find the value of ‘x’?
a) 16
b) 12
c) 20
d) 10
e) None of these
5) Quantity I: Total number of black colour caps is what percentage less than the total number of caps in bag R?
Quantity II: Total number of green colour caps is what percentage less than the total number of caps in bag S?
Quantity III: Total number of red colour caps is what percentage more than the total number of caps in bag T?
Note: The options represent the relations of Quantity I __ Quantity II __ Quantity III
A) >
B) <
C) =
D) ≤
E) ≥
a) A, C
b) B, D
c) E, B
d) B, B
e) C, B
Directions (Q. 6 – 10): Each question contains a statement followed by Quantity I and Quantity II. Read the contents clearly and answer your questions accordingly.
6) Quantity I: The shopkeeper sold an article at 10 % discount on marked price and he gains 20 %. If the marked price of the article is Rs. 400, then the cost price is?
Quantity II: The shopkeeper marks the price of the book Rs. 350 and his profit % is 15%. Find the cost price of the book, if he allows a discount of 8%?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
7) Quantity I: A and B started a business by Rs. 4800 and Rs. 6400 respectively. A invested only 5 months and they divided their shares after a year. The ratio of profit of A and B is 3 : 8. Then how many months B invested the money?
Quantity II: P and Q invested in the ratio of 5 : 8. P invested the money for 8 months. The ratio of profit of P and Q is 1 : 2. Then, how many months Q invested the money?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
8) Quantity I: Ravi can swim at 10 km/hr in still water. The river flows at 6 km/hr and it takes 6 hours more upstream than downstream for the same distance. How far is the place?
Quantity II: A man can row 20 km/hr in still water and the river is running at 8 km/hr. If the man takes 4 hr to row to a place and back, how far is the place?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
9) Quantity I: The SI on a certain sum of money for 5 years at 8 % per annum is Rs. 7500. Then the principle is?
Quantity II: The CI on a certain sum of money for 2 years at 20 % per annum is Rs. 8800. Then the principle is?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
10) A box contains 7 black balls, 5 pink balls and 4 yellow balls.
Quantity I: If 3 balls are drawn randomly, then the probability of getting at least one pink balls?
Quantity II: If 2 balls are drawn randomly, then the probability of getting both the balls is either black or yellow?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
Answers:
Directions (1-5):
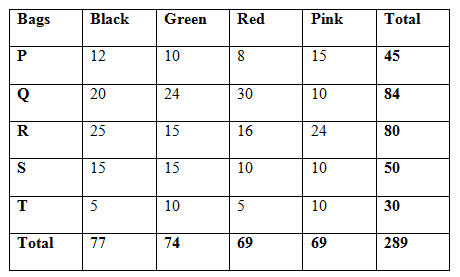
Bag P:
Number of pink colour caps is 15 which is 150% of the number of green colour caps. Number of black colour caps is 80% of pink colour caps. One cap is taken and the probability of getting a pink colour cap is 1/3.
Number of pink colour caps = 15
Number of green colour caps = (15/150) * 100 = 10
Number of black colour caps = (80/100) * 15 = 12
Let us take the number of red colour caps be x,
Total caps in bag P = 15+10+12+x = 37 + x
Probability of one pink cap = 15C1/(37+x)C1 = 1/3
15/(37 + x) = 1/3
45 = 37 + x
= > x = 45 – 37 = 8
Total = 45
Number of black, pink, green and red colour caps is 12, 15, 8 and 10 respectively
Bag Q:
The ratio of the number of black colour caps to the pink is 5: 6. The ratio of the number of pink colour caps to red is 4: 5. The ratio of the number of red colour caps to green is 3: 1. Two caps are taken and the probability of getting one pink and one red colour caps is 120/581.
Ratio of number of black, pink, red and green colour caps
Black : Pink : Red : Green
5 : 6 : 6 : 6
4 : 4 : 5 : 5
3 : 3 : 3 : 1
(5*4*3): (6*4*3): (6*5*3) : (6*5*1)
Ratio of number of black, pink, red and green colour caps
= 60: 72: 90: 30
= 20: 24: 30: 10
= 10: 12: 15: 5
Probability of one pink and one red colour caps
= 15xC1 *12xC1 /(10x+12x+15x+5x)C2 = 120/581
= > [(15x*12x)*2]/(42x*(42x-1)) = 120/581
= > x/(14*(42x-1))= 1/581
= > 581x = 588x – 14
= > 7x = 14
= > x = 2
Number of black, pink, red and green colour caps is 20, 24, 30 and 10 respectively.
Total = 84
Bag R:
Total number of caps is 35 more than the total number of caps in bag P. Total number of pink and red colour caps is 50% of the total number of caps. Number of pink colour cap is 150 percentage of the number of red colour caps. The number of green colour caps is 60% of the number of black colour caps.
Total = 35 + 45 = 80 caps
Number of pink and red colour caps = (50/100) * 80
= 40 caps
Number of pink colour caps = (150/100) * Number of red colour caps
Ratio of pink to red colour caps = 3: 2
Number of pink colour caps = 40*(3/5) = 24
Number of red colour caps = 40*(2/5) = 16
Number of black and green colour caps = (50/100) * 80 = 40 caps
Number of green colour caps = (60/100)*Number of black colour caps
Ratio of green to black colour caps = 3: 5
Number of green colour caps = 40*(3/8) = 15
Number of black colour caps = 40*(5/8) = 25
Number of black, pink, green and red colour caps is 25, 24, 15 and 16 respectively
Bag S:
Number of pink colour caps is equal to the number of red colour caps and 5 caps less than the number of green colour caps. Total number of caps in the bag is 5 more than bag P. one cap is taken and the probability of getting a black colour cap is 3/10.
Total = 45 + 5 = 50 caps
Number of green colour caps = x
Number of pink colour caps = Number of red colour caps = x – 5
Number of black colour caps = y
Probability of getting a black colour cap = yC1/50C1 = 3/10
y/50 =3/10
y = 15
Remaining = 50 – 15 = 35
= > x + (x -5) + (x -5) = 35
3x = 45
= > x = 15
Number of pink, black, green and red colour caps is 10, 15, 15 and 10 respectively.
Bag T:
Total number of caps in the bag is 66 (2/3)% of the total number of caps in the bag P. Number of black colour caps is one-sixth of the total number of caps and is equal to the number of red colour caps. One ball is taken and the probability of getting a green colour caps is 1/3.
Total = 66 (2/3)% of Total caps in bag P
= 200/300 * 45
= 2/3*45 = 30 caps
Number of black colour caps = 30 * (1/6) = 5 = Number of red colour caps
Number of green colour caps = x
Probability of getting a green colour cap = xC1/30C1 = 1/3
= > x/30 = 1/3
= > x = 10 caps
Number of pink colour caps = 30 – 10- 5 – 5 = 30 – 20 = 10 caps
Number of black, pink, green and red colour caps is 5, 10, 10 and 5 respectively
1) Answer: c)
Quantity I: Two caps taken randomly from the bag S. What is the probability of getting one red and one pink?
Required probability = (10C1*10C1)/50C2
= (10*10)/(50*49/(1*2))
= (10*10*2)/(50*49)
= 4/49
= 0.081
Quantity II: Two caps taken randomly from the bag T. What is the probability of getting both are pink colour?
Required probability = 10C2/30C2
= (10*9)/(30*29) = 3/29 = 0.1034
Quantity III: 7/20
7/20 = 0.35
Quantity I < Quantity II < Quantity III
2) Answer: b)
Quantity I: One cap is taken randomly from bag R, S and T. What is the probability of getting a black colour cap?
Required probability = (1/3) *(25/80 + 15/50 + 5/30)
= (1/3) * (5/16 + 3/10 + 1/6)
= (1/3) *((75+72+40)/240)
= (1/3) *(187/240)
= 187/720
= 0.2597
Quantity II: Two caps taken randomly from bag P. What is the probability of getting at least one green cap?
Required probability = 1 – Probability of none of the cap is green
= 1 – (35C2/45C2)
= 1 – ((35*34)/(45*44))
= 1 – 119/198
= 79/198
= 0.3989
Quantity I < Quantity II
3) Answer: b)
Total caps sold at 20% discount in bag Q = 84 * 25/100
= 84 * ¼ = 21
Total red caps sold at 20% discount in bag Q = 21 * 33 (1/3) %
= 21 * 1/3 = 7
Remaining red caps = 30 – 7 = 23
Required probability = (23C1/84C1)*(21C1/83C1)
= (23/84) * (21/83)
= 23/332
4) Answer: c)
Total caps in bag S after x green colour caps taken out = 50 – x
Total caps in bag T after x green colour caps added = 30 + x
Total caps in bag T after 2x red and x pink colour caps taken out
= (30 + x) – (2x + x)
= 30 – 2x
Total caps in bag S after 2x red and x pink colour caps added
= (50 – x) + (2x + x)
= 50 – x + 2x + x = 50 + 2x
In bag S, Probability of getting black colour cap is 1/6
15C1/(50+2x)C1 = 1/6
15/(50+2x) = 1/6
90 = 50 + 2x
2x = 40
= > x = 20 caps
5) Answer: d)
Quantity I: Total number of black colour caps is what percentage less than the total number of caps in bag R?
Required percentage = [(80 – 77)/80] * 100
= 3.75 %
Quantity II: Total number of green colour caps is what percentage more than the total number of caps in bag S?
Required percentage = [(69 – 50)/50] * 100
= (19/50) * 100
= 38%
Quantity III: Total number of red colour caps is what percentage more than the total number of caps in bag T?
Required percentage = [(69 – 30)/30] * 100
= (39/30)*100= 130%
Quantity I < Quantity II < Quantity III
Directions (Q. 6 – 10):
6) Answer: a)
Quantity I:
Selling price of the article = 400*(90/100) = Rs. 360
Cost price of the article
= > CP*(120/100) = 360
= > CP = 360*(100/120)
= > CP = Rs. 300
Quantity II:
Selling price of the book = 350*(92/100) = Rs. 322
Cost price of the book = 322*(100/115) = Rs. 280
Quantity I > Quantity II
7) Answer: e)
Quantity I:
According to the question,
(4800*5)/(6400*x) = (3/8)
24000/6400x = 3/8
24000*8 = 6400x*3
X = (32400*8)/(6400*3)
X = 10 months
Quantity II:
According to the question,
(5*8)/(8x) = (1/2)
X = 10 months
Quantity I = Quantity II
8) Answer: c)
Quantity I:
x/(10-6) – x/(10+6) = 6
x/4 – x/16 = 6
3x/16 = 6
X= 32 km
Quantity II:
Speed of still water (x) = 20 km/hr,
Speed of stream (y) = 8 km/hr
D = t*[(x2 – y2)/2x]
= > 4*[(202 – 82)/(2*20)]
= > 4*(400 – 64)/40
= > 4*(336/40)
= > 33.6 km
Quantity I < Quantity II
9) Answer: c)
Quantity I:
SI = (P*n*r)/100
7500 = (P*5*8)/100
P = (7500*100)/40 = Rs. 18750
Quantity II:
C.I = P*[(1 + (r/100))2 – 1]
8800 = P*[(1 + 20/100)2 – 1]
8800 = P*[(120/100)2 – 1]
8800 = P*[(24/20)2 – 1]
8800 = P*[(576/400) – 1]
8800 = P*[176/400]
P = (8800*400)/176 = Rs. 20000
Quantity I < Quantity II
10) Answer: a)
Quantity I:
Total probability n(S) = 16C3
Required probability n(E) = 1 – P(none is Pink)
Probability of getting none is Pink balls,
P(E) = n(E)/n(S) = 11C3/16C3
= > 33/112
Required probability = 1 – (33/112) = 79/112
Quantity II:
Total probability n(S) = 16C2
Required probability n(E) = 7C2 or 4C2
P(E) = n(E)/n(S) = 7C2 or 4C2 / 16C2
= > (21 + 6)/120 = 27/120
= > 9/40
Quantity I > Quantity II
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| NIACL AO Prelims – Reasoning | 10.00 AM |
| NIACL AO Prelims – Reasoning (Hindi) | 10.30 AM |
| NIACL AO Prelims – Quantitative Aptitude | 11.00 AM |
| NIACL AO Prelims – Quantitative Aptitude (Hindi) | 11.30 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| NIACL AO Prelims – English Language | 1.00 PM |
| SSC Practice Questions (Reasoning/Quantitative aptitude) | 2.00 PM |
| IBPS Clerk – GK Questions | 3.00 PM |
| SSC Practice Questions (English/General Knowledge) | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| SBI PO/IBPS Clerk Mains – Reasoning | 6.00 PM |
| SBI PO/IBPS Clerk Mains – Quantitative Aptitude | 7.00 PM |
| SBI PO/IBPS Clerk Mains – English Language | 8.00 PM |





