Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
Note: Dear IG ‘ians, Once Again IBPS Guide Team has brought you here with a New Innovative, to make you understand the questions more easier we have started providing Video Solutions for the questions. Practice here & click the link given below to check the video solutions of the same questions. Make use of it & thanks for your love.
[WpProQuiz 4608]Click Below for Video Solutions for these Questions
Directions (Q. 1 – 5): The questions below are based on the given Series-I. The series-I satisfy a certain pattern, follow the same pattern in Series-II and answer the questions given below.
1) I) 52, 54, 60, 72, 92, 122
II) 36……148. If 148 is nth term, then find the value of n?
a) 5
b) 4
c) 6
d) 7
e) 8
2) I) 72, 37, 38, 58, 117, 293.5
II) 16 …….. 881.25. If 881.25 is nth term, then what value should come in place of (n – 3)th term?
a) 83.5
b) 52
c) 64.5
d) 33
e) 75
3) I) 117, 115, 124, 96, 161, 35
II) 238 ……. 373. If 373 is nth term, then find the value of n?
a) 6
b) 7
c) 5
d) 8
e) 4
4) I) 534, 266, 132, 65, 31.5, 14.75
II) 890 …… 25.875. If 25.875 is nth term, then find the value of n?
a) 5
b) 4
c) 6
d) 7
e) 8
5) I) 216, 231, 255, 304, 402, 581
II) 752, 773 ……. 1453. If 1453 is nth term, then what value should come in place of (n-2)th term?
a) 896
b) 970
c) 914
d) 858
e) 962
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The given bar graph shows the percentage distribution of the area of six different shapes and the total area is 2200 cm2.
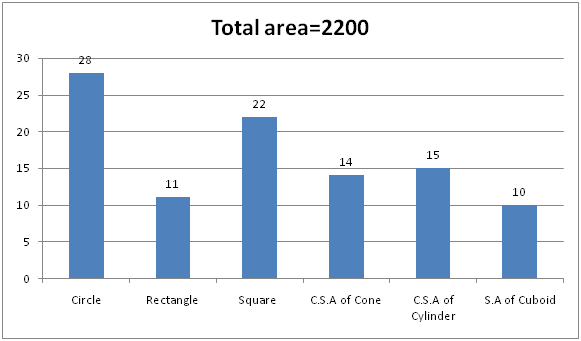
6) Find the perimeter of the rectangle?
Statement I: If the breadth of the rectangle is equal to the radius of the cone.
Statement II: Length of the cone is equal to the radius of the circle.
Statement III: Length of the rectangle is equal to the side of the square.
a) Only I and II are sufficient
b) Only II and III are sufficient
c) Either only III or I and II are sufficient
d) All I, II and III necessary to the answer the question
e) The question can’t be answered even with all I, II and III
7) Find the volume of sphere?
Quantity I: If the volume of the sphere is equal to the volume of the cone. Ratio of length and height of cone is 7 : 5 and the radius of the cone is equal to the side of the square.
Quantity II: If the radius of the circle is equal to the radius of the sphere.
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
8) What is the ratio of the volume of cylinder to the volume of the cuboid?
Statement I: Height of the cylinder is 120% of the radius of the cylinder. Base, Length and height of the cuboid are 12cm, 9cm and 20cm respectively.
Statement II: Base of the cuboid is same as the side of the square and length and height of the cuboid is equal. Radius of the cylinder is two-seventh of the radius of the circle.
a) Only I
b) Only II
c) Either I or II sufficient
d) All I and II necessary to the answer the question
e) The question can’t be answered even with all I and II
9) Find the height of the cone?
Statement I: If the radius of the cone is 50% of the radius of the circle.
Statement II: If the length of the cone is 150% of the radius of the circle.
a) Only I
b) Only II
c) Either I or II sufficient
d) All I and II necessary to the answer the question
e) The question can’t be answered even with all I and II
10) What is the difference between the area of rectangle and cuboid together and the area of the square and cylinder together?
a) 352 cm2
b) 362 cm2
c) 325 cm2
d) 382 cm2
e) None of these
Click Below for Video Solutions for these Questions
Answers :
Direction (1-5) :
1) Answer: d)
Series I Pattern:
52 is the first term
52 + (12 + 1) = 54
54 + (22 + 2) = 60
60 + (32 + 3) = 72
72 + (42 + 4) = 92
92 + (52 + 5) = 122
122 is 6th term
Series II Pattern:
36 is the first term
36 + (12 + 1) = 38
38 + (22 + 2) = 44
44 + (32 + 3) = 56
56 + (42 + 4) = 76
76 + (52 + 5) = 106
106 + (62 + 6) = 148
148 is 7th term. So, n = 7
2) Answer: d)
Series I Pattern:
72 is the first term
72*0.5 + 1 = 37
37*1 + 1 = 38
38*1.5 + 1 = 58
58*2 + 1 = 117
117*2.5 + 1 = 293.5
293.5 is 6th term
Series II Pattern:
16 is the first term
16*0.5 + 1 = 9
9*1 + 1 = 10
10*1.5 + 1 = 16
16*2 + 1 = 33 = (n-3)th term
33*2.5 + 1 = 83.5 = (n-2)th term
83.5*3 + 1 = 251.5 = (n-1)th term
251.5*3.5 + 1 = 881.25 = nth term
881.25 is nth term
The answer is, 33
3) Answer: b)
Series I Pattern:
117 is the first term
117 – (13 + 1) = 115
115 + (23 + 1) = 124
124 – (33 + 1) = 96
96 + (43 + 1) = 161
161 – (53 + 1) = 35
35 is 6th term
Series II Pattern:
238 is the first term
238 – (13 + 1) = 236
236 + (23 + 1) = 245
245 – (33 + 1) = 217
217 + (43 + 1) = 282
282 – (53 + 1) = 156
156 + (63 + 1) = 373
373 is 7th term. So, n = 7
4) Answer: c)
Series I Pattern:
534 is the first term
534 ÷ 2 – 1 = 266
266 ÷ 2 – 1 = 132
132 ÷ 2 – 1 = 65
65 ÷ 2 – 1 = 31.5
31.5 ÷ 2 – 1 = 14.75
14.75 is 6th term
Series II Pattern:
890 is the first term
890 ÷ 2 – 1 = 444
444 ÷ 2 – 1 = 221
221 ÷ 2 – 1 = 109.5
109.5 ÷ 2 – 1 = 53.75
53.75 ÷ 2 – 1 = 25.875
25.875 is 6th term. So, n = 6
5) Answer: e)
Series I Pattern:

Series II Pattern:

Direction (6-10) :
6) Answer: c)
From Statement I,
Area of the rectangle= (11/100)*2200= 242
CSA of cone = (14/100)*2200 = 308
(22/7)*r*l = 308
So, Statement I alone is not sufficient to the answer the question.
From Statement II,
Area of the circle = (28/100)*2200= 616
(22/7)*r*r = 616
Radius of circle r = 14
Length of the cone = 14 cm
So, Statement II alone is not sufficient to the answer the question.
From statement I and II,
(22/7)*r*14=308
Radius of the cone=7
Breadth of the rectangle=7
Area of the rectangle=l*7=242
l=242/7
Perimeter of the rectangle=2*[(242/7) + 7) = 582/7 cm
Statement I and II are sufficient to answer the question.
From Statement III,
Area of the square = (22/100)*2200= 484
Length of the rectangle=22
Area of the rectangle = (11/100)*2200=242
22*b =242
b=11
Perimeter of the rectangle = 2*(11+22) = 66 cm
Statement III are sufficient to answer the question.
7) Answer: c)
From quantity I,
Volume of the cone = (1/3)*(22/7)*r*r*h
CSA = (14/100)*2200 = 308
(22/7)*r*l = 308
rl = 98
Area of square = (22/100)*2200= 441
Side of the square= radius of the cone=22
l=98/22=49/11
Height of cone = (5*49/11)/7=35/11
Volume of the cone = (1/3)*(22/7)*22*22*(35/11) = 4840/3
Volume of the sphere = 4840/3
From quantity II,
Area of the circle = (28/100)*2200 = 616
(22/7)*r*r = 616
R2 = 196
r=14
Volume of sphere = (4/3)*(22/7)*r*r*r
= > (4/3)*(22/7)*14*14*14
= > 34496/3
Quantity II > Quantity I
8) Answer: a)
From Statement I,
Volume of the cuboid=12*9*20=2160
CSA of cylinder = (15/100)*2200=330
330=2*(22/7)*r*(120/100)*r
12r*r=525
r*r=175/4
r = (5/2)*√7
Volume of cylinder=(22/7)*r*r*h
= > (22/7)*(175/4)*(120/100)*(5/2)*√7
= > 825 (√7/2)
Required ratio= 825 (√7/2) : 2160
So, Statement I alone is sufficient to the answer the question.
From Statement II,
Side of the square=22
Base of the cuboid=22
Radius of circle=14
Radius of cylinder= (2/7)*14= 4
So, Statement II alone is not sufficient to the answer the question.
9) Answer: c)
From Statement I,
Radius of the circle=14
Radius of the cone = (50/100)*14=7cm
CSA of cone = (14/100)*2200=308 cm2
(22/7)*7*l=308
L=14 cm
14*14=h*h+7*7
196-49=h*h
147=h*h
h=√147 = 7√3 cm
So, Statement I alone is sufficient to the answer the question.
From statement II,
Radius of the circle=14
Length of the cone=14*(150/100)= 21
CSA of cone=308
(22/7)*21*r=308
r=14/3
441=h*h + (196/9)
h=√3773/3
So, Statement II alone is sufficient to the answer the question.
10) Answer: a)
Area of rectangle and cuboid = [(11+10)/100]*2200=462 cm2
Area of square and cylinder= [(22+15)/100]*2200=814 cm2
Difference=814-462=352 cm2





