Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4633]Click here to View Quantitative Aptitude Questions in Hindi
Directions (1-5): Study the following graph carefully and answer the given questions.
The line graph shows the speed of the stream (in km/hr).
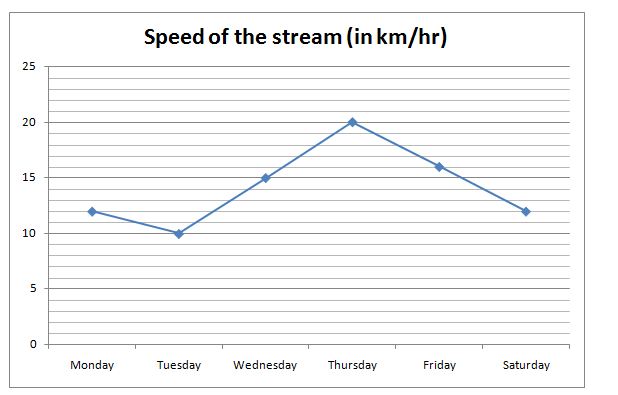
The table shows the distance (upstream and downstream) covered by different boats in same time on different days.
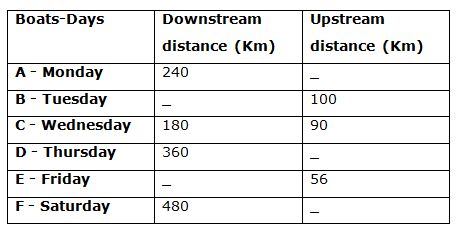
Note: Some values are missing, you need to calculate those values if required.
1) In Monday, Sanjana and Ranjana start swimming simultaneously from the two opposite ends of a lake at a speed is same as the boat A’s speed in still water. Sanjana swims along the stream and Ranjana swims against the stream. The distance between the ends is 1200 m and the time taken by Ranjana to swims the given distance is 48 secs more than that of Sanjana. Then what is the distance covered by boat A in upstream?
a) 240 km
b) 320 km
c) 144 km
d) 288 km
e) 120 km
2) If the speed of boat C in still water is 12.5% more than the speed of boat D in still water and the downstream distance covered by boat E is 40 km more than twice the upstream distance covered by boat D, then find the speed of boat E on Friday?
a) 40 km/hr
b) 32 km/hr
c) 28 km/hr
d) 24 km/hr
e) 30 km/hr
3) Find the ratio of the upstream distance covered by boat D to the downstream distance covered by boat E?
Statement I: If the upstream speed of boat D half of the downstream speed of boat E which is 40 km/hr
Statement II: The upstream distance covered by boat D is 20 km less than the half of the downstream distance covered by boat E
Statement III: The time taken to cover upstream distance by boat E is 1 hour more than the downstream distance covered by boat D which is 6 hour.
a) Only II
b) Either I or III
c) Any of the two
d) All the three together
e) None of these
4) Quantity I: Find the speed of the boat B, if the downstream distance covered by boat B is twice the upstream distance covered by boat B
Quantity II: Find the average speed of downstream and upstream of boat F to cover the given distance, if the downstream distance covered by boat F is twice the upstream distance covered by boat F
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity I = Quantity II (or) Relationship cannot be determined
d) Quantity I < Quantity II
e) Quantity I ≤ Quantity II
5) Find the ratio of upstream speed of boat A to the speed of boat D, if the downstream speed of boat A, C and D is same?
a) 2: 3
b) 4: 5
c) 6: 7
d) 9: 8
e) None of these
Directions (6 – 10): The questions below are based on the given Series-I. The series-I satisfy a certain pattern, follow the same pattern in Series-II and answer the questions given below.
6)
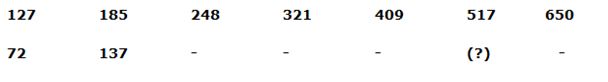
a) 513
b) 497
c) 459
d) 475
e) 502
7)
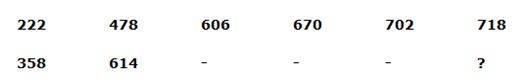
a) 726
b) 782
c) 834
d) 794
e) 854
8)
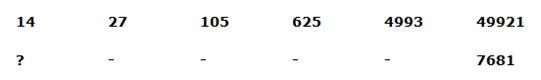
a) 5
b) 4
c) 2
d) 3
e) 6
9)
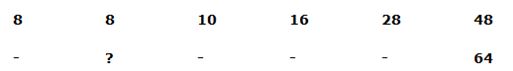
a) 16
b) 18
c) 24
d) 28
e) 12
10)
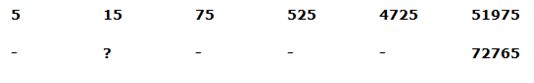
a) 21
b) 24
c) 18
d) 27
e) 33
Answers:
Directions (1-5):
1) Answer: c)
Let us take boat, Sanjana and Ranjana’s speed be x km/hr,
1200/[(x-12)*5/18] – 1200/[(x+12)*5/18] = 48
1200 * 18/5 [1/(x-12) – 1/(x+12)] = 48
90 [(x+12 –x +12)/(x2 – 122)] = 1
90*24 = x2 – 122
2160 = x2 – 144
= > x2 = 2160 + 144 = 2304
= > x = 48 km/hr
Time taken to cover downstream distance by boat A = 240/(48+12)
= 240/60
= 4 hours
Upstream distance covered by boat A = 4 * (48-12)
= 4 * 36
= 144 km
2) Answer: d)
Let us take the speed of boat C be x km/hr
According to the question,
180/(x+15) = 90/(x-15)
2/(x+15) =1/(x-15)
2*(x-15) = (x+15)
2x – 30 = x + 15
= > x = 45 km/hr
Speed of boat D in still water = 45 * [100/(100+12.5)]
= 45 * (100/112.5)
= 40 km/hr
Time taken to cover downstream distance by boat D in still water is
= > 360/(40+20)
= > 6 hours
Upstream distance covered by boat D in still water is
= > 6 *(40-20)
= 6 * 20 = 120 km
Downstream distance covered by boat E = 40 + (2*120)
= 280 km
Let us take the speed of boat E be y km/hr
According to the question,
280/(y+16) = 56/(y-16)
5/(y+16) =1/(y-16)
5y – 80 = y + 16
4y = 96
= > y = 24 km/hr
3) Answer: b)
From statement I: If the upstream speed of boat D half of the downstream speed of boat E which is 40 km/hr
Downstream speed of boat E = 40 km/hr
Upstream speed of boat D = 40/2 = 20 km/hr
On Friday,
Speed of stream on Friday = (Downstream speed – Upstream speed)/2
16 km/hr = (40 – Upstream speed)/2
Upstream speed of boat E = 40 – 32 = 8 km/hr
Time taken by boat E to cover 56 km upstream,
= > 56/8 = 7 hours
Downstream distance covered by boat E on Friday = 7 * 40 = 280 km
On Thursday,
Speed of stream on Thursday = (Downstream speed – Upstream speed)/2
20 = (Downstream speed – 20)/2
Downstream speed of boat D = 40 + 20 = 60 km/hr
Time taken by boat D to cover 360 km downstream,
= > 360/60 = 6 hours
Upstream distance covered by boat D on Thursday = 6 * 20 = 120 km
Required ratio = 280: 120 = 7: 3
Statement I alone is sufficient to answer the question.
From statement II: The upstream distance covered by boat D is 20 km less than the half of the downstream distance covered by boat E
Let us take downstream distance covered by boat E be x km
Upstream distance covered by boat D = (x/2 – 20)
On Thursday,
[360/(Speed of boat D + 20)] = [Upstream distance/(Speed of boat D – 20)]
[360/(Speed of boat D + 20)] = (x/2 – 20)/ (Speed of boat D – 20)]
On Friday,
[Downstream distance/(Speed of boat E+16)] = [56/(Speed of boat E – 16)]
X / (Speed of boat E+16) = [56/(Speed of boat E – 16)]
There is no information about speed of boat D and E. So we could not able to find the relation between downstream distance covered by boat E and the upstream distance covered by boat D
Statement II alone is not sufficient to answer the question.
Statement III: The time taken to cover upstream distance by boat E is 1 hour more than the downstream distance covered by boat D which is 6 hours.
On Thursday,
Time taken to cover downstream distance by boat D = 6 hours = Time taken to cover upstream distance by boat D
Downstream speed of boat D = 360/6 = 60 km/hr
Speed of stream on Thursday = (Downstream speed – Upstream speed)/2
20 = (60 – Upstream speed)/2
Upstream speed of boat D = 60 – 40 = 20 km/hr
Upstream distance of boat D = 20*6 = 120 km
On Friday,
Time taken to cover upstream distance by boat E = 7 hours = Time taken to cover downstream distance by boat E
Upstream speed of boat E = 56/7 = 8 km/hr
Speed of stream on Friday = (Downstream speed – Upstream speed)/2
16 = (Downstream speed – 8)/2
Downstream speed of boat E = 32 + 8 = 40 km/hr
Downstream distance of boat E = 40 * 7 = 280 km
Required ratio = 280: 120 = 7: 3
Statement III alone is sufficient to answer the question.
4) Answer: d)
From quantity I: Find the speed of the boat B, if the downstream distance covered by boat B is twice the upstream distance covered by boat B
Downstream distance covered by boat B = 100 * 2 = 200 km
200/(Speed of boat B+10) = 100/(Speed of boat B -10)
2 *(Speed of boat B -10) = (Speed of boat B+10)
Speed of boat B = 10+20 = 30 km/hr
From quantity II: Find the average speed of downstream and Upstream of boat F to cover the given distance, if the downstream distance covered by boat F is twice the upstream distance covered by boat F
Downstream distance covered by boat F = 2 * 240 = 480 km
480/(Speed of boat F + 12) = 240/(Speed of boat F – 12)
2* (Speed of boat F – 12) = (Speed of boat F + 12)
Speed of boat F = 12 + 24 = 36 km/hr
Downstream speed of boat F = 36 + 12 = 48 km/hr
Time taken by boat F to cover 480 km downstream = 480/48 = 10 hours
Upstream speed of boat F = 36 – 12 = 24 km/hr
Time taken by boat F to cover 240 km upstream = 240/24 = 10 hours
Average speed = Total distance/Total time
= (480+240)/(10+10)
= 720/20
= 36 km/hr
Hence, Quantity I < Quantity II
5) Answer: e)
Let us take the speed of boat C be x km/hr
180/(x+15) = 90/(x-15)
2*(x-15) = (x+15)
2x – 30 = x + 15
= > x = 45 km/hr
Downstream speed of boat C = Downstream speed of boat A = Downstream speed of boat D = (45+15) = 60 km/hr
Boat A,
Speed of stream = (Downstream speed – Upstream speed)/2
24 = (60 – Upstream speed)
Upstream speed of boat A = 60 – 24 = 36 km/hr
Boat D,
Speed of stream = (Downstream speed – Upstream speed)/2
40 = (60 – Upstream speed)
Upstream speed of boat D = 60 – 40 = 20 km/hr
Required ratio = 36: 20 = 9: 5
Directions (6-10):
6) Answer: b)
Series I Pattern:

Series II Pattern:
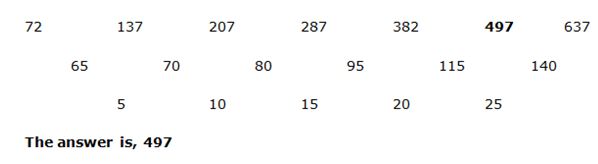
7) Answer: e)
Series I Pattern:
478 – 222 = 256
606 – 478 = 128
670 – 606 = 64
702 – 670 = 32
718 – 702 = 16
The pattern is, the difference of two numbers ÷ 2
Series II Pattern:
614 – 358 = 256
742 – 614 = 128
806 – 742 = 64
838 – 806 = 32
854 – 838 = 16
The answer is, 854
8) Answer: d)
Series I Pattern:
14*2 – 1 = 27
27*4 – 3 = 105
105*6 – 5 = 625
625*8 – 7 = 4993
4993*10 – 9 = 49921
Series II Pattern:
(7681 + 9)/10 = 769
(769 + 7)/8 = 97
(97 + 5)/6 = 17
(17 + 3)/4 = 5
(5 + 1)/2 = 3
The answer is, 3
9) Answer: c)
Series I Pattern:
The pattern is,
8 + (12 – 1) = 8
8 + (22 – 2) = 10
10 + (32 – 3) = 16
16 + (42 – 4) = 28
28 + (52 – 5) = 48
Series II Pattern:
64 – (52 – 5) = 44
44 – (42 – 4) = 32
32 – (32 – 3) = 26
26 – (22 – 2) = 24
24 – (12 – 1) = 24
The answer is, 24
10) Answer: a)
Series I Pattern:
5*3 = 15
15*5 = 75
75*7 = 525
525*9 = 4725
4725*11 = 51975
Series II Pattern:
72765/11 = 6615
6615/9 = 735
735/7 = 105
105/5 = 21
21/3 = 7
The answer is, 21
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| IBPS SO/NIACL AO Prelims – Reasoning | 10.00 AM |
| IBPS SO/NIACL AO Prelims – Reasoning (Hindi) | 10.30 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude | 11.00 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude (Hindi) | 11.30 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| IBPS SO/NIACL AO Prelims – English Language | 1.00 PM |
| SSC Practice Questions (Reasoning/Quantitative aptitude) | 2.00 PM |
| IBPS Clerk – GK Questions | 3.00 PM |
| SSC Practice Questions (English/General Knowledge) | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| SBI PO/IBPS Clerk Mains – Reasoning | 6.00 PM |
| SBI PO/IBPS Clerk Mains – Quantitative Aptitude | 7.00 PM |
| SBI PO/IBPS Clerk Mains – English Language | 8.00 PM |





