Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4746]
Click Here for IBPS Clerk Mains Online Mock Test
Direction (1 – 5): Study the following bar graph and answer the questions that follow:
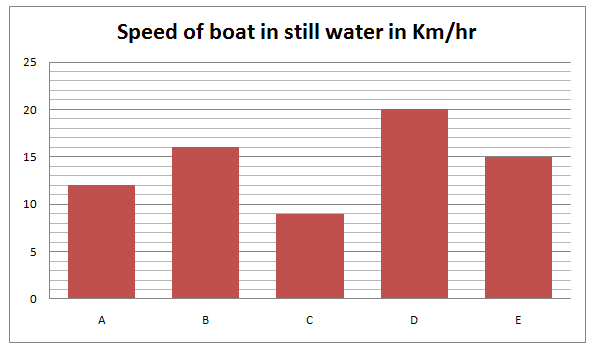
1) On a particular day, the time taken by boat A to cover 255 km downstream is 2 hours more than the time taken by boat D to cover 195 km upstream. Find the ratio of upstream speed to downstream speed in case of boat A on that particular day.
a) 1:3
b) 7:17
c) 5:19
d) 17:7
e) None of these
2) Boat B covered 756 km downstream on Saturday for which it took 6 hours less than that in which it covered half distance upstream on Sunday. On Sunday, speed of stream was 2 km/hr more than that on Saturday. Find the downstream speed of boat B on Sunday.
a) 22 km/hr
b) 19 km/hr
c) 25 km/hr
d) 23 km/hr
e) None of these
3) For boat C, its upstream speed is 6 km/hr on a particular day. Find the difference in time in covering 360 km by boats A and C on that particular day?
a) 9 hours
b) 5 hours
c) 6 hours
d) 7 hours
e) None of these
4) On a particular day, ratio of upstream speed to downstream speed of boat D is 3 : 7. It took 20 hours more to cover a distance upstream than same distance downstream by boat D. On that particular day, boat B covered same distance in how much time?
a) 5 hours
b) 19 hours
c) 16 hours
d) 21 hours
e) None of these
5) Upstream speed of boat E is 9 km/hr. How many more hours will it take to cover a distance of 315 km upstream than same distance downstream?
a) 25 hours
b) 21 hours
c) 18 hours
d) 20 hours
e) None of these
Directions (6-10): Study the following information and answer the given questions.
In 2015, Hari, Karna and Randy enter into a business with their investments in the ratio 4:3:7. After 3 months Hari withdrawn his whole amount, Karna withdrawn half of his amount and Randy doubles his amount. After another six months, Randy withdrawn 5/7th of his amount, Karna doubles his amount and Hari re-enter into the business with an amount equal to his initial amount.
6) The profit at the end of the year is Rs 14504 and if the profit is shared among all of them in the ratio of their investment, then the profit of Hari is how much less than that of Randy?
a) Rs 7289
b) Rs 9208
c) Rs 7098
d) Rs 8029
e) Rs 8390
7) All of them maintain their amount at the end of the first year as for another 24 months. Then what is the share of Hari if the overall profit for only last 24 months is Rs 32362?
a) Rs 10527
b) Rs 11768
c) Rs 11082
d) Rs 10862
e) Rs 12792
8) In 2016, Hari and Karna invested the same amount of money for 6 months and 8 months respectively. If the difference of their profit share is Rs 2320, then find the total profit of Hari and Karna in that year
a) Rs 15860
b) Rs 12080
c) Rs 16240
d) Rs 15220
e) Rs 14820
9) The sum of the total amount invested by Hari and Karna is Rs 46536 in 2015. If in 2016 Randy invested one third of the amount of what he invested in 2015, then find Randy’s investment in year 2016.
a) Rs 14625
b) Rs 15512
c) Rs 12709
d) Rs 15882
e) Rs 16826
10) If in 2016, the profit of Hari is increased by 10% and the profit of Karna is increased by 20% and the profit of Randy is decreased by 30%, then what is the ratio of profits of Hari, Karna and Randy in the year 2016?
a) 48:101:273
b) 88:108:271
c) 88:108:273
d) 81:128:273
e) 88:136:273
Answers:
1) Answer: b)
Let x km/hr is the speed of stream on that particular day.
So 255/(12+x) = 195/(20-x) + 2
Solve, x = 5 km/hr
So in case of boat A, ratio of speed upstream: downstream
= (12-5) : (12+5) = 7 : 17
2) Answer: d)
Let on Saturday, speed of stream is x km/hr, then on Sunday it is (x+2) km/hr
On Saturday it covered 756 km, so on Sunday it covered 756/2 = 378 km
So 756/(16+x) = 378/(16-(x+2)) – 6 ………(1)
Solve, x = 5 km/hr
So speed of stream on Sunday = (5+2) = 7 km/hr
So downstream speed of boat B = (16+7) = 23 km/hr
3) Answer: c)
Upstream speed of C = 6 km/hr, so speed of stream: 9 – x = 6, x = 3 km/hr
Downstream speed of boat C = 9+3 = 12 km/hr
Downstream speed of boat A = 12+3 = 15 km/hr
So difference in timings = 360/12 – 360/15 = 30 – 24 = 6 hours
4) Answer: a)
Let speed of stream on that day = x km/hr
So (20-x)/(20+x) = 3/7
Solve, x = 8 km/hr
So y/(20-8) – y/(20+8) = 20
Solve, y = 420 km
So required time = 420/(16+8) = 420/24 = 17.5 hours
5) Answer: d)
Upstream speed = 9, speed of boat = 15 km/hr,
so speed of stream = 15-9 = 6 km/hr
Downstream speed = 15+6 = 21 km/hr
So required time = 315/9 – 315/21 = 20 hours
Directions (6-10):
Given that, the investment ratio of Hari, Karna and Randy=4:3:7
Then profit ratio is obtained as follows:
Hari : Karna : Randy
(4*3 + 4*3) : {(3*3) + (3/2)*6+ [(3/2)*2]*3} : {(7*3) + [(2*7)*6] +
[(2/7)*14]*3}
24 : 27 : 117
8 : 9 : 39
6) Answer: d)
We have Profit ratio of Hari, Karna and Randy as 8:9:39
(i.e) Profit of Hari= 8x
Profit of Karna= 9x
Profit of Randy= 39x
Then total profit=8x+9x+39x=56x
Given that 56x=14504
x=259
Then profit of Hari= 8*259=2072
And Profit of Randy=39*259=10101
Required difference=10101-2072=Rs 8029
7) Answer: b)
At the end of first year, investment ratio is as follows:
Hari : Karna : Randy
4 : (3/2)*2 : (2/7)*14
4 : 3 : 4
Then total profit for last 24 months= 4x+3x+4x=11x
Then, 11x=32362
x=2942
Then share of Hari=4x=4*2942=Rs 11768
8) Answer: c)
Let x be the amount invested by Hari.
Then the ratio of profit of Hari and Karna in 2016 = 6x : 8x = 3 : 4
Then difference of their profit = 4x – 3x = x
(i.e) x= 2320
Then total profit= 7x=7*2320= Rs 16240
9) Answer: b)
Ratio of investment Hari, Karna and Randy in 2015=4:3:7
(i.e)Investment of Hari=4x
Investment of Karna=3x
Investment of Randy=7x
According to the question, 4x+3x=46536
7x=46536
x=6648
Thus Randy’s investment in 2015=7*6648=46536
Then, Randy’s investment in 2016=46536/3=Rs 15512
10) Answer: c)
Let the profit of Hari in the year 2015= 8x
Then profit of Hari in 2016= 8x*110/100=8.8x
Similarly the profit of Karna in 2016=9x*120/100 = 10.8x
And the profit of Randy in 2016= 39x*70/100 = 27.3x
Then Required ratio= 8.8x : 10.8x : 27.3x = 88:108:273
Click Here for IBPS Clerk Mains Online Mock Test
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| IBPS SO/NIACL AO Prelims – Reasoning | 10.00 AM |
| IBPS SO/NIACL AO Prelims – Reasoning (Hindi) | 10.30 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude | 11.00 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude (Hindi) | 11.30 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| IBPS SO/NIACL AO Prelims – English Language | 1.00 PM |
| SSC Practice Questions (Reasoning/Quantitative aptitude) | 2.00 PM |
| IBPS Clerk – GK Questions | 3.00 PM |
| SSC Practice Questions (English/General Knowledge) | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| SBI PO/IBPS Clerk Mains – Reasoning | 6.00 PM |
| SBI PO/IBPS Clerk Mains – Quantitative Aptitude | 7.00 PM |
| SBI PO/IBPS Clerk Mains – English Language | 8.00 PM |





