Dear Aspirants, Quantitative Aptitude plays a crucial role in Banking and all other competitive exams. To enrich your preparation, here we have provided New Pattern Aptitude Questions for IBPS Clerk Mains. Candidates those who are going to appear in IBPS Clerk Mains can practice these questions daily and make your preparation effective.
[WpProQuiz 4673]Click Here for IBPS Clerk Mains Online Mock Test
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 3): Study the following graph carefully and answer the given questions.
Preethi and Sharma can complete a work in 30 working days and 20 working days respectively with their full efficiencies. Preethi does work on Tuesday, Thursday and Saturday while Sharma does the work on Monday, Wednesday and Friday. Sunday is always off and Preethi takes Thursday off in 1st week and 3rd week while Sharma takes Saturday off in the week when Preethi does not take off. If Sharma started the work in 2nd December which falls on Monday followed by Preethi on the next day and so on (i.e. they work collectively in alternate days), then the work will be completed in ‘x’ days.
Note: Only two week-off is allowed by each of them excluding Sunday and no one takes week – off in the fifth week of the month.
1) Find the value of ‘x’ in the given paragraph?
a) 30
b) 20
c) 24
d) 28
e) 36
2) Reeta and Karna can completes the work individually in (x+16) days and (x-4) days. If they started working alternatively, Reeta works on 1st day with 100% more than her original efficiency and Karna works on 2nd day with 50% more than his original efficiency, then find the total number of days taken to complete double the work
a) 12
b) 18
c) 20
d) 16
e) 8
3) Pipe P and Q can fill an empty tank in (x+6) and (x-4) hours respectively. Pipe P fills the tank in 1st hour and empty the tank in 2nd hour and so on. If Pipe Q opened at 8.30 am and pipe P has been opened at 11.50 am. At what time three-fifth of the tank filled?
a) 8.14 pm
b) 7.50 pm
c) 9.20 pm
d) 8.30 pm
e) 9.10 pm
Directions (4 – 7): The questions below are based on the given Series-I. The series-I satisfy a certain pattern, follow the same pattern in Series-II and find the wrong number in the series –II.
4) I. 198, 210, 234, 282, 378, 570
II. 248, 260, 284, 332, 428, 618
a) 332
b) 428
c) 284
d) 618
e) 260
5) I. 2, 6, 28, 174, 1400, 14010
II. 9, 20, 84, 510, 4088, 40880
a) 4088
b) 20
c) 40880
d) 84
e) 510
6) I. 209, 332, 505, 778, 1201, 1824
II. 121, 230, 389, 647, 1057, 1666
a) 230
b) 647
c) 389
d) 1057
e) 1666
7) I. 88, 44, 44, 66, 132, 330, 990
II. 96, 48, 48, 72, 144, 360, 1008
a) 48
b) 72
c) 144
d) 360
e) 1008
Directions (8 – 10): Read the following information carefully and answer the given questions.
There are 400 students in a school in which 25% girls. All of them like at least one of the three different fruits viz. Mango, Apple and Papaya.
Boys: 10% likes Mango and Papaya together not Apple. 5% likes all the three fruits and 25% likes only Apple. 15% likes only Papaya.
Girls: 20% likes only Papaya and 15% likes Mango and Papaya but not Apple. 20% likes only Mango.
8) Find the ratio of the number of boys like Mango to the number of girls like Apple?
Statement I: 10% of boys like Apple and Papaya but not Mango
Statement II: 20% of boys like only Mango
a) Statement I alone is sufficient to answer the question
b) Statement II alone is sufficient to answer the question
c) Either statement I alone or II alone is sufficient to answer the question
d) Both the statements I and II together are not necessary to answer the question
e) Both the statements I and II together are necessary to answer the question
9) If 20% of girls like Mango and Apple and 15% of girls like Only Apple. 50% of boys like Mango.
Quantity I: Find the number of boys like Apple and Papaya but not Mango
Quantity II: Find the number of girls like Apple and Papaya but not Mango
Quantity III: If the number of girls like Mango and Apple but not Papaya is 2 more than the number of girls like Apple and Papaya but not Mango, then find the number of girls like all the three fruits.
Which of the following should be placed in the blank spaces of the expression “Quantity I__ Quantity II___Quantity III” from left to right with respect to the above statements?
a) >, >
b) <, >
c) <, <
d) >, <
e) None of these
10) If the 20% of boys and 15% of girls like only Mango and Only Apple respectively, then find the difference between the number of boys and girls like at least two fruits.
a) 75
b) 90
c) 80
d) 110
e) 55
Answers :
Directions (1 – 3):
LCM of 20 and 30 = 60
Total work = 60 units
Preethi’s per day work = 2 units
Sharma’s per day work = 3 units
December month consists of 31 days
Working days (5 Monday’s, 5 Tuesday’s, 4 Wednesday’s, 4 Thursday’s, 4 Friday’s and 4 Saturday’s)
Preethi takes week-off on 1st and 3rd week of the month
Sharma takes week-off on 2nd and 4th week of the month
If they work in all the days of the week (No week-off), they would complete 15 units
If they take week-off in the week, then their one day work subtracted from 15 units. We got one week’s total work.
1st week:
1st day (Monday) – Sharma completes 3 units
2nd day – Preethi completes 2 units
3rd day – Sharma completed 3 units
4th day – Preethi week-off
5th day – Sharma completes 3 units
6th day – Preethi completes 2 units
Total units completed at the end of 1st week is 13 units
(Or)
Total units completed at the end of 1st week = 15 – (Preethi’s work)
= 15 – 2 = 13 units
Similarly 2nd week,
Sharma takes week-off
Total units completed at the end of 2nd week = 15 – (Sharma’s work)
= 15 – 3 = 12 units
1st and 3rd week is same and 2nd and 4th week is also same
Total units completed at the end of four weeks = (13+12+13+12)
= 50 units
Remaining = 60- 50 = 10 units
In 5th week has only three days in December month
30th – Monday – Sharma completes 3 units
31st – Tuesday – Preethi completes 2 units
Total work completed at the end of December month is (50+3+2) 55 units
On January, 1st week:
1st day – Wednesday – Sharma completes 3 units
2nd day – Thursday – Preethi completes 2 units
Total work completed in (5+5+5+5+2+2) 24 days
= > x = 24 working days
1) Answer: c)
x = 24 days
2) Answer: d)
Reeta can completes the whole work in (x+16) 40 days
Karna can completes the whole work in (x-4) 20 days
LCM of 40 and 20 = 40 units
Total work = 40 units
Reeta’s per day work = 1 units
Reeta’s 100% more efficiency = 1*200/100 = 2 units
Karna’s per day work = 2 units
Karna’s 50% more efficiency = 2 * 150/100 = 3 units
1st cycle (2 days) = 2+3 = 5 units
8th cycle (16 days) = 5*8 = 40 units
Total work completed in 16 days.
3) Answer: a)
Pipe P takes (x+6) 30 hours to fills an empty tank in first hour and empty the full tank in second hour and so on
Pipe Q takes (x-4) 20 hours to fills the tank
LCM of 20 and 30 = 60
Total work = 60 units
Required units to fill the tank is 3/5*60 = 36 units
Pipe P = 2 units
Pipe Q = 3 units
Pipe Q fills the tank in 3 hours 20 minutes = (3*3)+(3*20/60)
= 9 +1
= 10 units
Remaining = 36 – 10 = 26 units
Pipe P and Q fills the remaining tank,
1st hour = (P + Q) = 3+2 = 5 units
2nd hour = (Q – P) = 3 – 2 = 1 unit
1st cycle (2 hours) = 6 units filled
4th cycle (8 hours) = 6*4 = 24 units
Remaining = 26 – 24 = 2 units
Remaining 2 units filled in 2/5 hour = 24 minutes
Three fifth of the tank filled at (11.50 am + 8 hours 24 minutes) = 8.14 pm
Direction (4-7) :
4) Answer: d)

5) Answer: c)
Series –I pattern:
2 * 2 + 2 = 6
6 * 4 + 4 = 28
28 * 6 + 6 = 174
174 * 8 + 8 = 1400
1400 * 10 + 10 = 14010
Series –II pattern:
9 * 2 + 2 = 20
20 * 4 + 4 = 84
84 * 6 + 6 = 510
510 * 8 + 8 = 4088
4088 * 10 + 10 = 40890
The wrong number is, 40880
6) Answer: b)

7) Answer: e)
Series- I pattern:
88 * 0.5 = 44
44 * 1 = 44
44 * 1.5 = 66
66 * 2 = 132
132 * 2.5 = 330
330 * 3 = 990
Series –II pattern:
96 * 0.5 = 48
48 * 1 = 48
48 * 1.5 = 72
72 * 2 = 144
144 * 2.5 = 360
360 * 3 = 1080
The wrong number is, 1008
Directions (8 – 10):
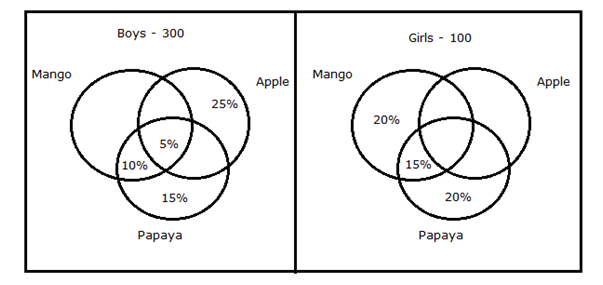
8) Answer: a)
Number of girls like Apple = 100 – (Number of girls not like apple)
= 100 – [100*(20+15+20) %]
= 100 – (100*55/100)
= 100 – 55 = 45
From statement I,
Number of boys like Mango = 300 – (Number of boys not like Mango)
= 300 – [300*(15+20+10) %]
= 300 – (300 * 45/100)
= 300 – 135
= 165
Required ratio = 165: 45
= 11: 5
Hence, Statement I alone is sufficient to answer the question
From statement II,
Number of boys like Mango = 300 – (Number of boys not like Mango)
= 300 – [300*(20+10+5+No of boys like Mango & Apple but not Papaya)]
From that, we could not able to find the ratio because there is no information about the number of boys like Mango & Apple but not Papaya.
Hence, Statement II alone is not sufficient to answer the question
9) Answer: d)
20% of girls like Mango and Apple and 15% of girls like Only Apple. 50% of boys like Mango.
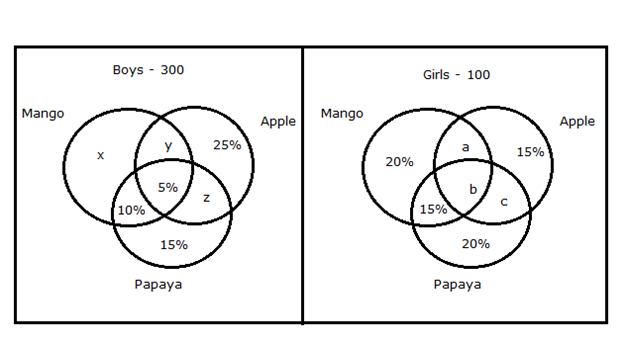
Boys:
(x+y+5%+10%) = 50%
(x+y) = 50% – 15% = 35%
= > z = 100% – (10%+15%+5%+25%+35%)
= > z = 100% – 90% = 10%
Girls:
(a + b) = 20%
= > c = 100% – (20%+15%+20%+15%+20%)
= > c = 100% – 90% = 10%
Quantity I: Find the number of boys like Apple and Papaya but not Mango
Required total = z = 10% of 300
= 10/100 * 300
= 30
Quantity II: Find the number of girls like Apple and Papaya but not Mango
Required total = c= 10% of 100
= 10/100 * 100
= 10
Quantity III: If the number of girls like Mango and Apple but not Papaya is 2 more than the number of girls like Apple and Papaya but not Mango, then find the number of girls like all the three fruits.
Number of girls like Mango and Apple = 20/100 * 100
= 20
(a + b) = 20
The number of girls like Mango and Apple but not Papaya = 2 + the number of girls like Apple and Papaya but not Mango
= > a = c+ 2
= > a = (10/100 * 100) + 2
= > a = 12
Quantity I > Quantity II < Quantity III
10) Answer: a)

Number of boys like at least two fruits = 300 – (Boys like only one fruit)
= 300 – [300*(20%+15%+25%)]
= 300 – (300*60/100)
= 300 – 180
= 120
Number of girls like at least two fruits = 100 – (Girls like only one fruit)
= 100 – [100*(20+15+20)%]
= 100 – (100*55/100)
= 100 – 55
= 45
Required difference = 120 – 45
= 75
Click Here for IBPS Clerk Mains Online Mock Test
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| IBPS SO/NIACL AO Prelims – Reasoning | 10.00 AM |
| IBPS SO/NIACL AO Prelims – Reasoning (Hindi) | 10.30 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude | 11.00 AM |
| IBPS SO/NIACL AO Prelims – Quantitative Aptitude (Hindi) | 11.30 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| IBPS SO/NIACL AO Prelims – English Language | 1.00 PM |
| SSC Practice Questions (Reasoning/Quantitative aptitude) | 2.00 PM |
| IBPS Clerk – GK Questions | 3.00 PM |
| SSC Practice Questions (English/General Knowledge) | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| SBI PO/IBPS Clerk Mains – Reasoning | 6.00 PM |
| SBI PO/IBPS Clerk Mains – Quantitative Aptitude | 7.00 PM |
| SBI PO/IBPS Clerk Mains – English Language | 8.00 PM |





