Dear Readers, Bank Exam Race for the Year 2018 is already started, To enrich your preparation here we have providing new series of Practice Questions on Quantitative Aptitude – Section. Candidates those who are preparing for IBPS PO Mains 2018 Exams can practice these questions daily and make your preparation effective.
[WpProQuiz 4051]Directions (Q. 1 – 5): Each question contains Quantity I and Quantity II. Read the contents clearly and answer your questions accordingly.
1)
Quantity I: The length of the rectangle is thrice the side of a square whose area is 324 Sq. m. The breadth of the rectangle is 10 m less than the length of the rectangle. Find the area of rectangle?
Quantity II: The perimeter of a rectangle is 212 m. The difference between the length and breadth of the rectangle is 18 m. Find the area of a rectangle?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
2)
Quantity I: The ratio between the downstream and upstream speed of the boat is 4 : 3. The boat travels 64 km downstream in 8 hours. Find the speed of the boat in still water
Quantity II: The boat travels 72 km downstream in 8 hours. The speed of the stream is 3 km/hr. Find the speed of the boat in still water?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
3)
Quantity I: Two trains are moving in opposite directions at 40 km/hr and 60 km/hr. Train lengths are 250 m and 200 m respectively. The time taken by the slower train to cross the faster train is?
Quantity II: The length of Mumbai express is 170 m and that of Sathapthi express is 180 m. These two trains are running in the same direction with the velocities of 60 km/hr and 80 km/hr respectively. The time taken by them to cross each other is?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
4)
Quantity I: The present age of Anitha is 15 years more the present age of Rahul. After 10 years the ratio of ages of Rahul and Anitha will be 7 : 10, then find the age of Anitha, after 4 years?
Quantity II: The present age of Naveen is thrice the present age of Priyanka. The ratio between the present ages of Gourav and Priyanka is 5 : 3. If the age of Gourav after 6 years will be 21 years, then find the sum of the present age of Naveen, Priyanka and Gourav?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
5) A person invested a sum of Rs. 35600 in two schemes A and B which offers interest at the rate of 18% and 12 % respectively. If the total interest received from these schemes after one year is Rs. 5340 then,
Quantity I: Sum of money invested in scheme A?
Quantity II: Sum of money invested in scheme B?
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
Directions (Q. 6 – 10) Study the following information carefully and answer the given questions.
The following table shows the number of 4 different color balls in 6 different bags.
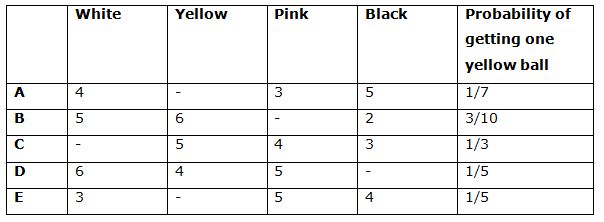
6) If 3 balls are taken out randomly from bag A, then find the probability of getting at least one pink ball from bag A?
a) 247/425
b) 78/217
c) 199/364
d) 123/289
e) None of these
7) If 4 balls are taken out randomly from bag C, then find the probability of getting different color balls from bag C?
a) 12/91
b) 45/77
c) 33/125
d) 127/245
e) None of these
8) If 4 balls are taken out randomly from bag D, then find the probability of getting 2 pink balls from bag D?
a) 56/121
b) 123/285
c) 92/157
d) 70/323
e) None of these
9) Find the ratio between the total number of balls in bag B to that of bag E?
a) 5: 6
b) 4: 3
c) 7: 8
d) 5: 4
e) None of these
10) Total number of pink balls in all the bags together is what percentage of total number of yellow balls in all the bags together?
a) 120 %
b) 80 %
c) 150 %
d) 100 %
e) 90 %
Answers:
Directions (1-5):
1) Answer: c)
Quantity I:
Area of the square = a2 = 324
Side of the square (a) = 18m
Length of the rectangle = 54m
Breadth= 44m
Area of the rectangle = 54*44= 2376 Sq. m
Quantity II:
The perimeter of a rectangle = 212 m
2(l + b) = 212
l + b = 106 —> (1)
l – b = 18 —> (2)
By solving the equation (1) and (2), we get,
Length = 62 m, Breadth = 44 m
Area of the rectangle = 62*44 = 2728 Sq. m
Quantity I < Quantity II
2) Answer: a)
Quantity I:
Downstream speed= 64/8 = 8 km/hr
Upstream speed= 8*(3/4) = 6 km/hr
Speed of boat in still water = ½ *(8+6) = 7 km/hr
Quantity II:
Downstream speed= 72/8= 9 km/hr
Downstream speed = Speed of boat in still water + speed of stream
Let the speed of boat be x
=> x + 3 = 9
=> x= 6 km/hr
Speed of boat in still water = 6 km/hr
Quantity I > Quantity II
3) Answer: c)
Quantity I:
T= D/S
T = (250 + 200)/[(40 + 60)*5/18]
T = 450/(100*(5/18)) = 16.2 sec
Quantity II:
T = D/S
T = (170 + 180)/[(80 – 60)*(5/18)]
T = 350/(20*(5/18))
T = 63 sec
Quantity I < Quantity II
4) Answer: c)
Quantity I:
Present age of Anitha = 15 + Present age of Rahul
After 10 years, The ratio of ages of Rahul and Anitha = 7 : 10(7x, 10x)
10x – 10 = 15 + 7x – 10
10x – 10 = 7x + 5
3x = 15
X = 5
The age of Anitha, after 4 years = 10x – 6 = 50 – 6 = 44 years
Quantity II:
The ratio of present age of Naveen and Priyanka = 3 : 1
The ratio of present age of Gourav and Priyanka = 5 : 3
The present age of Naveen, Priyanka and Gourav = 9 : 3 : 5
The age of Gourav, after 6 years = 21 years
The present age of Gourav = 15 years
5’s = 15
1’s = 3
Required sum = 17*3 = 51 years
Quantity I < Quantity II
5) Answer: e)
Percentage of interest received from these schemes
= 5340*100/35600
= 15%
By the rule of allegation,
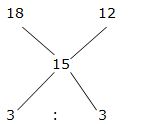
= > 1 : 1
2’s = 35600
1’s = 17800
Quantity I:
Sum of money invested in scheme A= Rs. 17800
Quantity II:
Sum of money invested in scheme B = Rs. 17800
Quantity I = Quantity II
Directions (6-10):
6) Answer: c)
Let the yellow ball be X,
Probability of getting one yellow ball = 1/7
XC1/(12 + X)C1 = 1/7
X/(12 + X) = 1/7
7X = 12 + X
6X = 12
X = 2
Yellow balls in bag A = 2 balls
Total probability = 14C3
The probability of getting at least one pink ball
= > 1 – P(none is pink ball)
Probability of getting none is pink ball
= > 11C3 /14C3 = 165/364
The probability of getting at least one pink ball
= > 1 – (165/364) = 199/364
7) Answer: a)
Let the white ball be X,
Probability of getting one yellow ball = 1/3
5C1/(12 + X)C1 = 1/3
5/(12 + X) = 1/3
15 = 12 + X
X = 3
The total white balls in bag C = 3
Total probability = 15C4
Required probability = 3C1 and 5C1 and 4C1 and 3C1
The probability of getting different color balls
= > [3C1 and 5C1 and 4C1 and 3C1]/15C4
= > 12/91
8) Answer: d)
Let the black ball be X,
Probability of getting one yellow ball = 1/5
4C1/(15 + X)C1 = 1/5
4/(15 + X) = 1/5
20 = 15 + X
X = 5
Total number of black balls = 5
Total probability = 20C4
Required probability = 5C2 and 15C2
The probability of getting 2 pink balls from bag D
= > (5C2 and 15C2)/20C4
= > 70/323
9) Answer: b)
Let the pink ball in bag B be X,
Probability of getting one yellow ball = 3/10
6C1/(13 + X)C1 = 3/10
6/(13 + X) = 3/10
13 + X = 20
X = 7
The total number of pink ball in bag B = 7 balls
Total balls in bag B = 5 + 6 + 7 + 2 = 20
Let the yellow ball in bag E be Y,
Probability of getting one yellow ball = 1/5
YC1/(12 + Y)C1 = 1/5
Y/(12 + Y) = 1/5
5Y = 12 + Y
4Y = 12
Y = 3
The total number of yellow ball in bag E = 3 balls
Total balls in bag E = 3 + 3 + 5 + 4 = 15
Required ratio = 20: 15 = 4: 3
10) Answer: a)
Let the pink ball in bag B be X,
Probability of getting one yellow ball = 3/10
6C1/(13 + X)C1 = 3/10
6/(13 + X) = 3/10
13 + X = 20
X = 7
The total number of pink ball in bag B = 7 balls
Total number of pink balls in all the bags together
= > 3 + 7 + 4 + 5 + 5 = 24
Let the yellow ball in bag A be Y,
Probability of getting one yellow ball = 1/7
YC1/(12 + Y)C1 = 1/7
Y/(12 + Y) = 1/7
7Y = 12 + Y
6Y = 12
Y = 2
Yellow balls in bag A = 2 balls
Let the yellow ball in bag E be Z,
Probability of getting one yellow ball = 1/5
ZC1/(12 +Z)C1 = 1/5
Z/(12 + Z) = 1/5
5Z = 12 + Z
4Z = 12
Z = 3
The total number of yellow ball in bag E = 3 balls
Total number of yellow balls in all the bags together
= > 2 + 6 + 5 + 4 + 3 = 20
Required % = (24/20)*100 = 120 %
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Current Affairs Quiz (Hindi) | 9.30 AM |
| IBPS PO Mains – Reasoning | 10.00 AM |
| IBPS PO Mains– Quantitative Aptitude | 11.00 PM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| IBPS PO Mains – English Language | 1.00 PM |
| IBPS PO/Clerk – GK | 3.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| IBPS Clerk Prelims – Reasoning | 6.00 PM |
| IBPS Clerk Prelims – Reasoning (Hindi) | 6.30 PM |
| IBPS Clerk Prelims – Quantitative Aptitude | 7.00 PM |
| IBPS Clerk Prelims – Quantitative Aptitude (Hindi) | 7.30 PM |
| IBPS Clerk Prelims – English Language | 8.00 PM |





