Important Computer Awareness Materials (Day-24) – Introduction of Computer Number System (part-2):
Dear Readers, IBPS Exams are approaching shortly, we all knew that Computer Awareness is one of the important section, which will help you to increase your score easily.
Many of our followers were asking us to provide Important Computer Awareness Notes along with the model questions, here we have planned to provide the Topic wise Important Computer Awareness Materials on Daily basis, and also we will provide MCQs based on these topics daily. Kindly follow us regularly and make use of it.
Introduction of Computer Number System (part-2)
There are many methods or techniques which can be used to convert numbers from one base to another. We’ll demonstrate here the following:
Decimal to Other Base System:
Steps
Step 1 – Divide the decimal number to be converted by the value of the new base.
Step 2 – Get the remainder from Step 1 as the rightmost digit (least significant digit) of new base number.
Step 3 – Divide the quotient of the previous divide by the new base.
Step 4 – Record the remainder from Step 3 as the next digit (to the left) of the new base number.
Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3.
The last remainder thus obtained will be the most significant digit (MSD) of the new base number.
Example:
Decimal Number: 2910
Calculating Binary Equivalent:
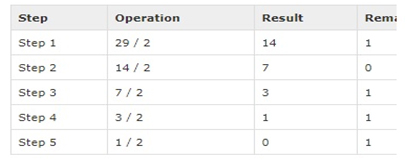
As mentioned in Steps 2 and 4, the remainders have to be arranged in the reverse order so that the first remainder becomes the least significant digit (LSD) and the last remainder becomes the most significant digit (MSD).
Decimal Number: 2910 = Binary Number: 111012.
Other base system to Decimal System:
Steps
Step 1 – Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the number system).
Step 2 – Multiply the obtained column values (in Step 1) by the digits in the corresponding columns.
Step 3 – Sum the products calculated in Step 2. The total is the equivalent value in decimal.
Example:
Binary Number: 111012
Calculating Decimal Equivalent:

Other Base System to Non-Decimal System:
Steps
Step 1 – Convert the original number to a decimal number (base 10).
Step 2 – Convert the decimal number so obtained to the new base number.
Example:
Octal Number: 258
Calculating Binary Equivalent:

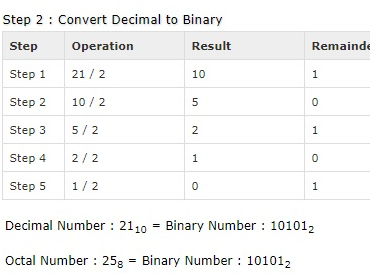
Shortcut method – Binary to Octal:
Steps
Step 1 – Divide the binary digits into groups of three (starting from the right).
Step 2 – Convert each group of three binary digits to one octal digit.
Example
Binary Number: 101012
Calculating Octal Equivalent:
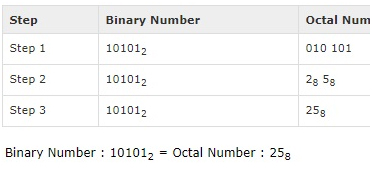
Shortcut method – Octal to Binary:
Steps
Step 1 – Convert each octal digit to a 3 digit binary number (the octal digits may be treated as decimal for this conversion).
Step 2 – Combine all the resulting binary groups (of 3 digits each) into a single binary number.
Example:
Octal Number: 258
Calculating Binary Equivalent:
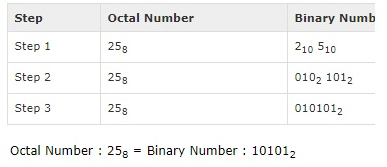
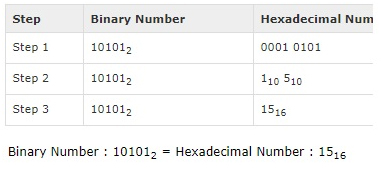
Shortcut method – Binary to Hexadecimal:
Steps
Step 1 – Divide the binary digits into groups of four (starting from the right).
Step 2 – Convert each group of four binary digits to one hexadecimal symbol.
Example:
Binary Number: 101012
Calculating hexadecimal Equivalent:
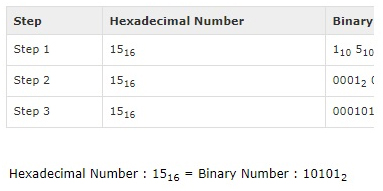
Shortcut method – Hexadecimal to Binary:
steps
Step 1 – Convert each hexadecimal digit to a 4 digit binary number (the hexadecimal digits may be treated as decimal for this conversion).
Step 2 – Combine all the resulting binary groups (of 4 digits each) into a single binary number.
Example:
Hexadecimal Number: 1516
Calculating Binary Equivalent:
Click Here for Computer Awareness Materials (Day-1 to Day-23)





