Page Contents
Mensuration Formulas PDF:
Mensuration formulas PDF Download is available here. Aspirants preparing for the various competitive exams will search for mensuration all formulas. In the quantitative aptitude section, there is a possibility for a few questions from the mensuration topic. So memorize these mensuration formulas PDF for CAT, TNPSC, banking, SSC & other exams.
In the quantitative aptitude section, there are many topics. In that mensuration is a topic that involves a lot of formula. To solve sums within the time boundary, you must memorize the mensuration maths formulas and also need to understand the concept. That is very essential. So we have provided mensuration formulas pdf. In mensuration for each geometric shape, there is a various formula. Without knowing the mensuration formula, you cannot find solutions for those problems. Many candidates will avoid this topic in their preparation, due to the lot of mensuration formula. But if you understand the concept and study in a clear manner, then the mensuration formula will be very easy to memorize. Then you will don’t get afraid of this topic. So utilize this mensuration formulas pdf.
Why Mensuration Formula is Essential?
Many candidates will skip the mensuration questions in the exams. The reason is they may don’t know the formula. if you know the formula, mostly all the mensuration problems are easy to solve. Nowadays, competitive exams are very difficult to crack. every year the cut-offs are reaching sky-high. The candidates are preparing under pressure to secure a government job. In this situation, you should leave no stones unturned in your preparation and practice. So don’t avoid any topic in your preparation. If you do not understand a topic, try it from basics and learn it. Only then you can score marks in all the topics. So, you can have the confidence to crack your dream exams. This is applicable for the mensuration topic as well. So, mensuration formulas pdf is essential.
Guidely Online Mock Test Series
List of Geometric Shapes:
There are various geometric shapes that we come across in daily life. The shapes may be of 2d or 3d. If you understand the concept, it is very simple to memorize all the mensuration formulas. Here a list of all the geometric shapes is available.
- Triangle
- Rectangle
- Square
- Trapezium
- Parallelogram
- Rhombus
- Quadrilateral
- Circle
- Cube
- Cuboid
- Cone
- Cylinder
- Sphere
- Pyramid
- Prism
For 2d geometric shapes, usually, there are formulas for area and perimeter. The mensuration formula 3d shapes include volume, curved surface area, and total surface area.
Quadrilateral – Mensuration Formulas PDF:
The quadrilateral is a 2d geometric shape. The quadrilateral will have totally 4 sides. The mensuration formula for the area of the quadrilateral is,
- Area of quadrilateral = 1/2 × Diagonal × (Sum of offsets)
we have added below some basic types of quadrilaterals. They are,
- Square
- Rectangle
- Parallelogram
- Rhombus
- Trapezium
The mensuration formula list of all these shapes is discussed below.
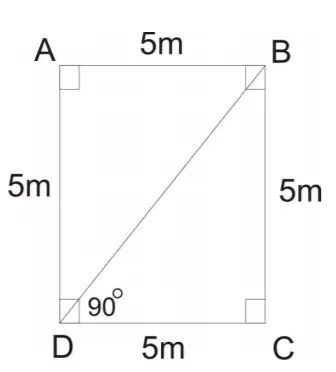
Square – Mensuration Formulas PDF:
The square will have equal 4 sides. Also, the opposite sides are parallel to each other. The mensuration formulas for the square are available.
- Area of square = a×a
- The perimeter of square = 4a
Here, a = side of the square.
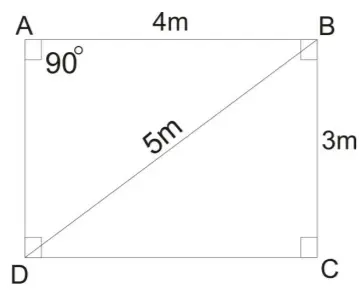
Rectangle – Mensuration Formulas PDF:
In a rectangle, the opposite sides are equal and parallel. But not all 4 sides are equal. The mensuration formula sheet for the rectangle is,
- Area of rectangle = lb
- Perimeter of rectangle = 2(l+b)
Here, l = length of rectangle and b = breadth of the rectangle.
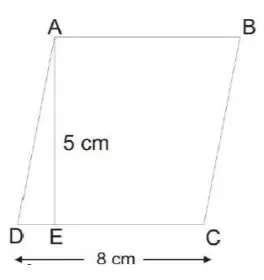
Parallelogram – Mensuration Formulas PDF:
In a parallelogram, the opposite sides are parallel and equal. But all 4 sides are not equal. Also, the angle of the corners is not at 90 degrees. Whereas in square and rectangle, the angle of corners is 90 degrees.
- Area of parallelogram = l × h
- Perimeter of parallelogram = 2(l+b)
Here, l = length or base of parallelogram. h = height of parallelogram.
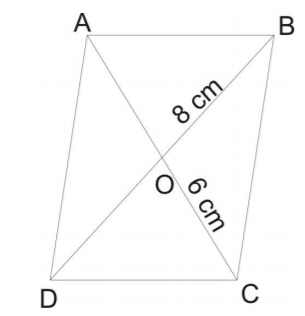
Rhombus – Mensuration Formulas PDF:
Rhombus is also a parallelogram. The main factor is that all 4 sides are equal in the rhombus. The mensuration formula chart for the rhombus is,
- Area of rhombus = d1 × d2 / 2
- The perimeter of rhombus = 4l
Here, d1 and d2 are the lengths of the diagonals. l is the side of the rhombus.
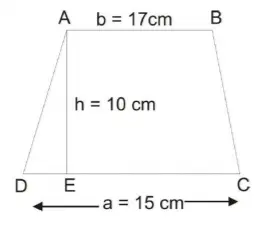
Trapezium– Mensuration Formulas PDF:
In trapezium, one set of opposite sides are parallel and unequal. The other set of opposite sides are not parallel.
- Area = 1 / 2 h(a+b)
- Perimeter = Sum of all sides
Here a and b are the top and bottom sides of the trapezium. h is the height of the trapezium.
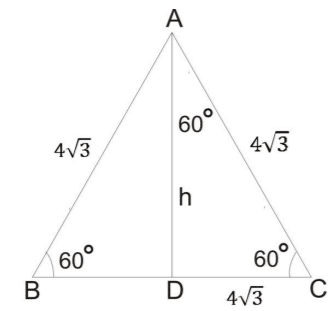
Triangle – Mensuration Formulas PDF:
Triangle is a 2d geometric shape with 3 sides. There are various types of triangles. They are,
- Equilateral triangle – all 3 sides are equal
- Isosceles triangle – two sides are equal
- Scalene triangle – No sides are equal
The mensuration formula sheet for the triangle are,
- Area of triangle = (1/2) x b x h
Here b and h are the base and height of the triangle respectively.
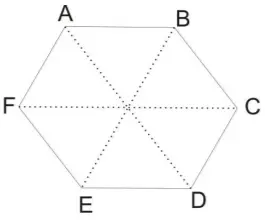
Regular Hexagon – Mensuration Formulas PDF:
Hexagon is a shape with 6 sides. If all 6 sides are equal, then it is known as a regular hexagon. The formula for the regular hexagon is,
- Area of a regular hexagon = 6 x √3 /4 x (side)2
- Perimeter of a regular hexagon = 6 x (side)
Circle – Mensuration Formulas PDF:
The maths mensuration formulas table pdf for the circle shape is,
- Circumference of a circle = 𝜋 x diameter
- Diameter of circle = 2r
- Area of a circle = 𝜋 x r x r
Here r is the radius of the circle.
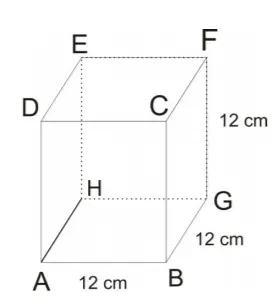
Cube– Mensuration Formulas PDF:
Cube is a 3d shape of a square. In the cube all the length, breadth, and height are equal. The mensuration formula for bank exams also includes all 3d shapes. So refer to the mensuration formulas for the cube here.
- Volume of a cube = (side)3
- Total surface area of a cube = 6 × (side)2
- Diagonal of cube = √3 x (side)
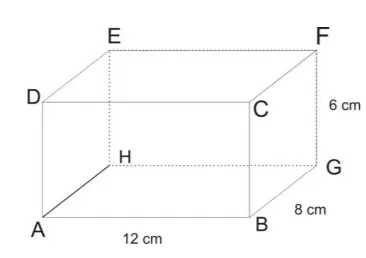
Cuboid – Mensuration Formulas PDF:
It is a 3d shape of a rectangle. The mensuration formulas for the cuboid are,
- Volume of a cuboid = (length × breadth × height) = lbh
- Total surface area of cuboid = 2(lb + bh + hl)
Cylinder – Mensuration Formulas PDF:
The cylinder is a 3d figure. The mensuration formula pdf for the cylinder are,
- Area of curved surface = (perimeter of base) x height = 2𝜋rh
- Total surface area = 2𝜋r(r + h)
- Volume = 𝜋 x r x r x h

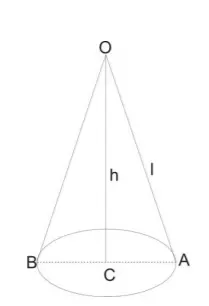
Cone – Mensuration Formulas PDF:
The mensuration formulas pdf for the cone are,
- Curved surface area = 𝜋rl
- Total surface area = 𝜋r(r + l)
- Volume of cone = (1/3) x 𝜋 x r x r x h
Here l is the slant height of the cone.
Sphere – Mensuration Formulas PDF:
For sphere, the formulas are,
- Surface area = 4𝜋 x r x r
- Volume of sphere = (4/3) x 𝜋 x r x r x r
Similarly, the formulas can be derived for the hemisphere. You can refer to the mensuration formula PDF with illustrations.
Candidates use some mensuration formula tricks to remember easily. Also if you understand the concept, it is easy to memorize all the mensuration formulas.
Also for TNPSC exams are also it will be useful. In group 4 exams, the mensuration questions are at a basic and easy level. So study all in mensuration formula PDF.
Here we have also given the links for general awareness, current affairs, static GK preparation. You can also Practice quizzes and test your level of preparation.
FAQs:
Here we have added some FAQs regarding the mensuration formulas pdf.
Q: What is the easiest way to learn mensuration formulas?
A: If you understand the concept of geometric shapes, then it is easy for you to memorize all mensuration formulas.
Q: Differentiate between 2D and 3D mensuration?
A: In 2D, the shapes of the objects orient in 2 axes. Ex: square, rectangle, triangle. But in 3D, the shapes of the objects orient in 3 axes. Ex: Cube, Cuboid, cone, etc.