Numerical Ability is one of the heebie-jeebie topics which consuming more time in Banking exams. There is no doubt Numerical Ability questions will be a complex of mathematics. Once you got a right strategy to solve the Numerical Ability questions then you can easily manage your time. To get a maximum mark in this section the aspirants need to know the tricks of Numerical Ability. Don’t worry if you are a basic learner of banking exam Read and understand the tricks of Numerical Ability. Here you can find the set of the question with important tricks to solve Numerical Ability questions.
Daily Practice Questions for Numerical Ability:
Practice only gives the perfection. Numerical Ability topic will cover the basic arithmetics such as addition, subtraction multiplication, and division. To become a master in Numerical Ability section start your practice with free Daily “20-20 QA”. The direct link is given for landing page. Practice more on Numerical Ability and crack your upcoming bank exams.
Daily Numerical Ability Questions – Click Here to Practice
Important Tricks to Solve Numerical Ability Questions:
Topics From Numerical Ability:
- Shortcut Tricks to find the Square of Numbers
- Easy Method to Take Square Root for a Number
- Shortcut for the Multiplication of 2 Digit & 3 Digit Numbers
- Shortcut for the Multiplication of 3 Digit & 4 Digit Numbers
- Easy Method to Take Cube Root of Numbers
- Shortcut Rules for Basic Multiplication
- Shortcut Rules for Basic Subtraction
- Shortcut Rules for Basic Division
Numerical Ability – Shortcut Tricks to find the Square of Numbers:
SQUARE OF NUMBERS:
- Square of a number is the product obtained by multiplying a number by itself
2×2 = 4
11×11 = 121 - To find the square of two-digit numbers (10-99) we can consider the following steps
1) Let the 2-digit number be = AB
2) Now to find AB2
3) Unit digit of square = B2
4) Ten’s digit of square = 2×A×B (+ Carry if any from the previous step)
5) The rest of the digits of square = A2 (+ Carry if any from the previous step)
FOR EXAMPLE
672 = ?
AB2 = 672
STEP 1:
B2 = 72 = 4 9 Here “9” is the unit digit and “4” is carry
- 672 = _ _ _ 9
STEP 2:
[2×A×B] + Carry from previous step i.e., 4
2×A×B = 2×6×7 = 84
Add Carry ‘4’ with the above ‘84’ we get [84+4= 88]
Therefore at the end of the 2nd Step
From Step 1, here “8” is the unit digit and “8” is carry
- 672 = _ _ 8 9
STEP 3:
A2 = 62 = 36
There is a carry of ‘8’ from the previous step
Therefore, [36+8] = 44
The final answer is 672 = 4 4 8 9
To find the square of a number which is a multiple of ‘5’
AB2 = [A× next number] B2
252 = [2×3] 52
= [6] 25 = 625
i.e., AB2 where B=5
AB2 = [A× next number] B2
For example, 852 = [8×9] 25 = 7225
1152 = [11×12] 25 = 13225
1552 = [15×16] 25 = 24025
This method can be followed for all numbers divisible by 5
Easy Method to Take Square Root for a Number
Numerical Ability – SQUARE ROOT
POINTS TO REMEMBER:
- When 22 = 4, then √4 = 2
- Here 4 is the square of 2
- 2 is the square root of 4
- A Square of a number can never end with 2, 3, 7 and 8
Table 1:
| One’s digit of a square | One’s digit of the square root |
| 1 | 1 or 9 |
| 4 | 2 or 8 |
| 5 | 5 |
| 6 | 4 or 6 |
| 9 | 7 or 3 |
To find the square of a number which is a multiple of ‘5’
252 = [2×3] 52
= [6] 25 = 625
i.e., AB2 where B=5
AB2 = [A× next number] B2
For example, 852 = [8×9] 25 = 7225
1152 = [11×12] 25 = 13225
1552 = [15×16] 25 = 24025
This method can be followed for all numbers divisible by 5
TYPE 1:
To find the square root of a 3-digit number
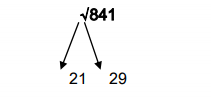
EXAMPLE: √841
STEP 1: Consider the one’s digit of the given number i.e., 1
From Table 1, if the one’s digit of the square is ‘1’ then the square root would either end with ‘1’ or ‘9’
STEP 2: Always ignore the ten’s digit of the given number
STEP 3: Now the remaining number other than the one’s and the ten’s digit in the given number is ‘8’. Consider a square-root of a square which is nearer to as well as lesser than ‘8’.
Here it is ‘4’ which is nearer to as well as lesser than ‘8’. Hence the square root of 4 i.e., ‘2’ is taken.
STEP 4: we already know the one’s digit of the square root to be either 1 or 9 from STEP 1
Therefore the square root of ‘841’ lies between 21 and 29
 STEP 5:
STEP 5:
Take a number divisible by ‘5’ between 21 and 29, that is ‘25’
252 = [2×3] 25 = 625
Now 625 < 841
252 is itself lesser than 841. Then 212 will be much lesser than 841.
Therefore, the remaining option is ‘29’
√841 = 29
TYPE 2:
To find the square root of a 4-digit number
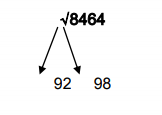
EXAMPLE: √8464
STEP 1: Consider the one’s digit of the given number i.e., 4
From Table 1, if the one’s digit of the square is ‘4’ then the square root would either end with ‘2’ or ‘8’
STEP 2: Always ignore the ten’s digit of the given number
STEP 3: Now the remaining numbers other than the one’s and the ten’s digit in the given number is ‘84’
Consider a square-root of a square which is nearer to as well as lesser than ‘84’.
Here it is ‘81’ which is nearer to as well as lesser than ‘84’. Hence the square root of 81 i.e., ‘9’ is taken.
STEP 4: we already know the one’s digit of the square root to be either 2 or 8 from STEP 1
Therefore the square root of ‘8464’ lies between 92 and 98
 STEP 5:
STEP 5:
Take a number divisible by ‘5’ between 92 and 98, that is ‘95’
952 = [9×10] 25 = 9025
Now 9025 > 8464
952 is itself greater than 8464. Then 982 will be much greater than 8464
Therefore, the remaining option is ‘92’
√8464 = 92
TYPE 3:
To find the square root of a 5-digit number
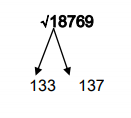
EXAMPLE: √18769
STEP 1: Consider the one’s digit of the given number i.e., 9
From Table 1, if the one’s digit of the square is ‘9’ then the square root would either end with ‘3’ or ‘7’
STEP 2: Always ignore the ten’s digit of the given number
STEP 3: Now the remaining numbers other than the one’s and the ten’s digit in the given number is ‘187’
Consider a square-root of a square which is nearer to as well as lesser than ‘187’
Here it is ‘169’ which is nearer to as well as lesser than 187. Hence the square root of 169 i.e., ‘13’ is taken
STEP 4: we already know the one’s digit of the square root to be either 3 or 7 from STEP 1
Therefore the square root of ‘18769’ lies between 133 and 137
 STEP 5:
STEP 5:
Take a number divisible by ‘5’ between 133 and 137, that is ‘135’
1352 = [13×14] 25 = 18225
Now 18225 < 18769
1352 is itself smaller than 18769. Then 1332 will be much lesser than 18769. Therefore, the remaining option is ‘137’
√18769 = 137
Shortcut for the Multiplication of 2 Digit & 3 Digit Numbers – Numerical Ability
MULTIPLICATION OF 2-DIGIT NUMBERS (10-99):
EXAMPLE 1:
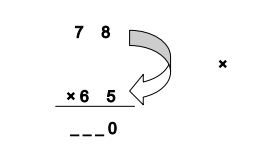
78×65 =?
GIVEN:
N1 = 78; N2 = 65
SOLUTION:
- STEP 1: One’s digit of the product is obtained by multiplying the one’s digits of N1 and N2
One’s digit of product = [One’s digit of N1 × One’s digit of N2]
= [8×5] = 40
‘4’ is taken as carry to the Step 2 i.e., C1 = 4
STEP 2:
Ten’s digit of product = [Ten’s digit of N1×One’s digit of N2] + [One’s digit of N1×Ten’s digit of N2] + C1
= [7×5] + [6×8] + 4
= 35 + 48 + 4
= 87
‘8’ is taken as the carry to Step 3 i.e., C2 = 8

Add the Products of the above 2-steps. At the end of Step 2 we have
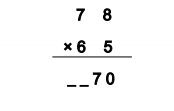
STEP 3:
To calculate the hundredth and the thousandth digit of the product
= [Ten’s digit of N1 × Ten’s digit of N2] + C2
= [7×6] + 8
= [42] + 8
= 50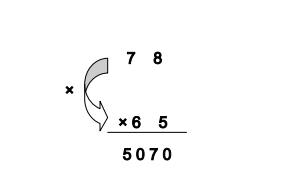
Therefore, 78×65 = 5070.
Shortcut for the Multiplication of 2 Digit & 3 Digit Numbers – Numerical Ability
MULTIPLICATION OF NUMBERS BETWEEN (90-99):
The product can be determined by a simple multiplication and a subtraction.
EXAMPLE:
98 × 97 = ?
Here, these numbers are nearer to ‘100’ in the number system.
So their difference from ‘100’ is considered, i.e., [D1=100-98=02] & [D2=100-97=03]
GIVEN:
No.1 = 98; No.2 = 97
Difference, D1 = 02; D2 = 03
SOLUTION:
The multiplication is done between 2-digit numbers so the product will definitely be a 4-digit number.
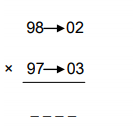
The one’s and ten’s digit of the product will be the product of D1 and D2
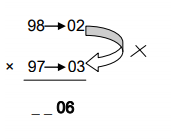
i.e., D1×D2 = 02×03 = 06
Similarly, the hundredth and thousand digit of the product will be the difference between No.2 and D1. i.e., [No.2-D1 = 97-02=95]
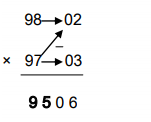
Therefore, 98×97 = 9506
This method can be applied to multiply 2-digit numbers whose difference from ‘100’ can be multiplied with each other easily.
88 × 89 = ?
Here, No.1=88; No.2=89; D1=100-88=12; D2=100-89=11
Here, 12 × 11 = 132, we know that the product is a 4-digit number so ‘1’ is taken as carry
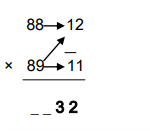
For the hundredth and thousand digits of the product, No.2 – D1 = 89-12=77
Now we have one carry from the previous step ‘1’, that is added to this difference [77+1=78]
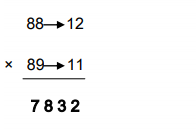
Therefore, 88×89=7832
MULTIPLICATION OF NUMBERS BETWEEN (101-110):
Here the product can be determined by a simple multiplication and an addition.
EXAMPLE:
108 × 107 = ?
Here, these numbers are nearer to ‘100’ in the number system.
So their difference from ‘100’ is considered, i.e., [D1=108-100=08] &
[D2=107-100=07]
GIVEN:
No.1 = 108; No.2 = 107
Difference, D1 = 08; D2 = 07
SOLUTION:
The multiplication is done between 3-digit numbers below 200(<200) so the product will definitely be a 5-digit number.
Here, the method is same as that of 2-digit multiplication except for a small change.
STEP 1: Product of D1 and D2 is same i.e., [D1×D2=08×07=56]
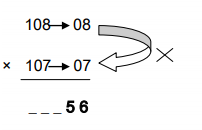
STEP 2: Since the numbers are greater than 100, the sum of No.2 and D1 is taken
[No.2+D1=107+08=115]
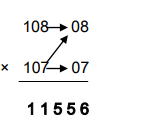
Therefore, 108×107=11556
Similarly, if D1 and D2 are more than 10, then the carry over from the product of D1×D2 is added to the sum of No.2+D1
For example, 111×112=?
Here D1=11; D2=12 (>10)
Therefore, D1×D2=11×12=132
In step 2, No.2+D1=112+11=123+carry=123+1=124
So, 111×112=12432
Numerical Ability – Shortcut for the Multiplication of 3 Digit & 4 Digit Numbers
MULTIPLICATION OF NUMBERS BETWEEN (900-999):
The product can be determined by a simple multiplication and a subtraction.
EXAMPLE:
998 × 997 = ?
Here, these numbers are nearer to ‘1000’ in the number system.
So their difference from ‘1000’ is considered, i.e., [D1=1000-998=002] & [D2=1000-997=003]
GIVEN:
No.1 = 998; No.2 = 997
Difference, D1 = 002; D2 = 003
SOLUTION:
The multiplication is done between 3-digit numbers so the product will definitely be a 6-digit number.
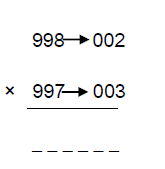
The one’s, ten’s and hundredth digit of the product will be the product of D1 and D2
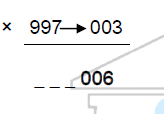
i.e., D1×D2 = 002×003 = 006
Similarly, the 1st 3 digits of the product will be the difference between No.2 and D1. i.e., [No.2-D1 = 97-02=95]

Therefore, 998×997 = 995006
This method can be applied to multiply 3-digit numbers whose difference from ‘1000’ can be multiplied with each other easily.
988 × 989 = ?
Here, No.1=988; No.2=989; D1=1000-988=12; D2=1000-989=11
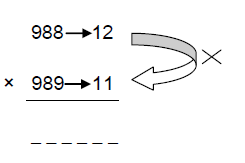
Here, 12 × 11 = 132
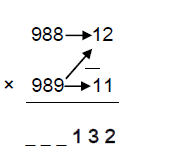
For the 1st 3 digits of the product, No.2 – D1 = 989-12= 977
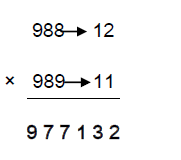
Therefore, 988×989=977132
MULTIPLICATION OF NUMBERS BETWEEN (1001-1010):
Here the product can be determined by a simple multiplication and an addition.
EXAMPLE:
1008 × 1007 = ?
Here, these numbers are nearer to ‘1000’ in the number system.
So their difference from ‘1000’ is considered, i.e., [D1=1008-1000=008] & [D2=1007-1000=007]
GIVEN:
No.1 = 1008; No.2 = 1007
Difference, D1 = 008; D2 = 007
SOLUTION:
The multiplication is done between 4-digit numbers so the product will definitely be a 7-digit number.
Here, the method is same as that of 3-digit multiplication except for a small change.
STEP 1: product of D1 and D2 is same i.e., [D1×D2=008×007=056]
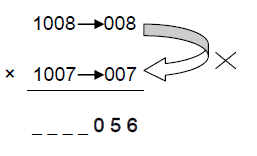
STEP 2: Since the numbers are greater than 1000, the sum of No.2 and D1 is taken
[No.2+D1=1007+08=1015]
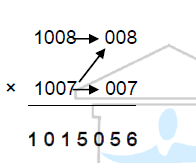
Therefore, 1008×1007=1015056
Fast and Easy Method to Take Cube Root – Numerical Ability
POINTS TO REMEMBER:
- When 23 = 8, then (8)1/3 = 2
- Here 8 is the cube of 2
- 2 is the cube root of 8
Table 1:
| One’s digit of a cube | One’s digit of the cube root |
| 1 | 1 |
| 2 | 8 |
| 3 | 7 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 3 |
| 8 | 2 |
| 9 | 9 |
| 0 | 0 |
TYPE 1: To find the cube root of a 4-digit Number
EXAMPLE: (9261)1/3
STEP 1: Consider the one’s digit of the given number i.e., 1
From Table 1, if the one’s digit of the cube is ‘1’ then the cube root would also end with ‘1’
STEP 2: Always ignore the ten’s and the hundredth digits of the given number i.e., ignore ‘2’ and ‘6’ in the given number
STEP 3: Now the remaining number other than the one’s, ten’s and the hundredth digit in the given number is ‘9’
Consider a cube-root of a cube which is nearer to as well as lesser than ‘9’.
Here it is ‘8’ which is nearer to as well as lesser than ‘9’. Hence the cube root of 8 i.e., ‘2’ is taken
STEP 4: we already know the one’s digit of the cube root is 1 from STEP 1
Therefore the cube root of ‘9261’ is 21
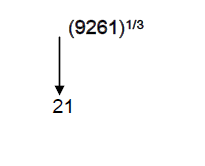
Therefore (9261)1/3 = 21
TYPE 2:
To find the cube root of a 5-digit number
EXAMPLE: (32768)1/3
STEP 1: Consider the one’s digit of the given number i.e., 8
From Table 1, if the one’s digit of the cube is ‘8’ then the cube root would end with ‘2’
STEP 2: Always ignore the ten’s and the hundredth digits of the given number i.e., ‘6’ and ‘7’ here
STEP 3: Now the remaining numbers other than the one’s, ten’s and the hundredth digits in the given number is ‘32’
Consider a cube-root of a cube which is nearer to as well as lesser than ‘32’.
Here it is ‘27’ which is nearer to as well as lesser than ‘32’. Hence the cube root of 27 i.e., ‘3’ is taken
STEP 4: we already know the one’s digit of the cube root to be 2 from STEP 1
Therefore the cube root of ‘32768’ is 32
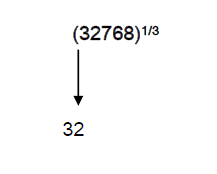
Therefore (32768)1/3 = 32
Shortcut Numerical Ability Rules for Basic Multiplication
Type-1: If the unit figure is same and the sum of the tens figure is 10, then follow the below method.
General Shortcut Method:
[Tens fig. × Tens fig. + Unit fig.] [Unit fig × Unit fig]
Example:
86 × 26 = [8 × 2 + 6] [6 × 6] = [22] [36]; so answer is: 2236.
Note: Here, the unit figure denotes the number that present in the ones digit (6, 6), and tens figure denotes the number that present in the tens digit (8, 2).
Type-2: If the sum of the unit figure is 5 and the tens figure are equal. Then follow the below method.
General Shortcut Method:
[(Tens figure)2 + ½ × Tens figure] [Unit fig. × Unit fig]
Example:
83 × 82 = [82 + ½ × 8] [ 3 × 2 ] = [68] [06] So the answer is: 6806
Type-3: If the unit figures are same and the sum of tens figures is 5.
General Shortcut Method:
[Tens fig × Tens fig + ½ × Unit fig] [(Unit fig.)2]
Example:
36 × 26 = [3 × 2 + ½ × 6] [62]
= [9] [36]; Answer is 936.
Type-4: If the unit figures are 5 and difference between the tens figures is 1 then the rule is,
General Shortcut Method: [(Larger tens fig + 1) × (Smaller tens fig)] [75]
Example:
35 × 45 = [(4 + 1) × 3] [75]
= [15] [75]; So the Answer is, 1575.
MULTIPLICATION BY 11 WITH ANY NUMBER AND ANY DIGITS – Numerical Ability
TWO DIGIT NUMBERS:
TYPE I: When the sum of the one’s and ten’s digit of the number is less than 10 (i.e. 0 to 9)
For example, 43×11 where the sum of the digits is less than 10, [4+3=7] this method can be used.
Now 43×11
4 _ 3
The one’s and the ten’s digit of the number will be the last and the first digit of the product
respectively.
43×11
4 7 3
The ten’s digit of the product will be sum of the digits of the number, here [4+3=7]
Therefore, 43 × 11 = 473.
Similarly, 36 × 11 = 396, where [3+6=9]
53 × 11 = 583, where [5+3=8]
TYPE II: When the sum of the one’s and ten’s digit of the number is either 10 or more than 10 (i.e. 10 or 10<)
For example, 28 ×11 where the sum of the digits is 10, [2+8=10] this method can be used.
Now 28×11
_ _ 8
The one’s digit of the number will be the one’s digit of the product.
28×11
_ 0 8
The ten’s digit of the product will be sum of the digits of the number, here [2 + 8 = 1 0]↓
Carryover
The hundredth digit of the product will be the sum of ten’s digit of the number and the carry over.
[2 + 1 = 3]
Therefore, 28×11
3 0 8
Similarly, 85 × 11 = 935 → {9[8+1] 3[8+5=13] 5}
99 × 11 = 1089 → {10[9+1] 8[9+9=18] 9}
THREE DIGIT NUMBERS:
TYPE I (Sum of digits < 10):
For example:
352 × 11
Here the sum of the digits, 3+5=8 & 5+2=7⇓
Both the sums are less than 10
Now, 352 × 11
3 _ _ 2
Similar to 2-digit multiplication the first and the last digit of the number will be the first and the last
digit of the product.
The ten’s digit of the product = [One’s digit of the no. + Ten’s digit of the no.]
= [5 + 2 = 7]
352 × 11
3 _ 7 2
The hundredth digit of the product = [Hundredth digit of the no. + Ten’s digit of the no.]
= [3 + 5 = 8]
352 × 11
3 8 7 2
Therefore, 352×11 = 3872.
Similarly, 236 × 11 = 2596 → {2 5[2+3=5] 9[3+6] 6}
123 × 11 = 1353 → {1 3[1+2=3] 5[2+3] 3}
TYPE II (Sum of digits >10):
For example:
756 × 11
Here the sum of the digits, 7+5=12 & 5+6=11⇓
Both the sums are more than 10
Now, 756 × 11
_ _ _ 6
The one’s digit of the product is same as the one’s digit of the number.
Ten’s digit of the product = [One’s digit of no. + Ten’s digit of no.]
= [5 + 6 = 1 1]
Carry over 1
756 × 11
_ _ 1 6
Hundredth digit of the product = [Ten’s digit of no.+ Hundredth digit of no.] + Carry over 1
= [7 + 5] + 1 = 1 3
Carry over 2
756 × 11
_ 3 1 6
Thousand digit of the product = [Hundredth digit of the number + Carry over 2] = [7 + 1 = 8]
756 × 11
8 3 1 6
Therefore, 756 × 11 = 8316
Similarly, 999 × 11 = 10989 → {10[9+1] 9[9+9+1=19] 8[9+9=18] 9}
Shortcut Numerical Ability Rules for Basic Subtraction
Rule-I: Borrowing and Paying Back Method:
This method is the quickest method of subtraction. This method is also called equal additions method.
Example (1): Suppose we have to subtract 55 from 91. Mentally we have to increase the number to be subtracted to the nearest multiple of 10 i.e., increase 55 to 60 by adding 5 to it. Mentally increase the other quantity by the same amount i.e., by 5. Therefore, the problem is 96 minus 60 i.e., our answer is 96 – 60= 36.
Example (2): Sometimes it is useful to increase the number to be subtracted to the nearest multiple of 100.
for example 442 – 179. Therefore 179 becomes 200 by adding 21 and 442 becomes 463 by adding 21. Then the problem becomes 463 – 200= 263. Now we see that 463 – 200 is easier than 442 – 179. The result is same as 263.
Example (3): Another example is 2326 – 1875. Here 1875 becomes 2000 by adding 125 and 2326 becomes 2451 by adding 125. The number becomes 2451 – 2000= 451. Here the subtraction 2451 – 2000 is easier than the subtraction 2326 – 1875. The answer of both is same 451.
Example (4): The subtraction of 3786 – 2998. Here 2998 becomes 3000 by adding 2 and 3786 becomes 3788 by adding 2. The problem of 3788 – 3000 is easier than 3786 – 2998 and our answer is 788. This answer is same for both the problems.
Rule: II. Double Column Addition and Subtraction Method:
This following method works when there is a series of additions and subtractions are to be performed in a line.
Example (1):
1026
– 4572
+5263
– 2763
+8294
_____________
Explanation: We have to look the signs given before the numbers and then start adding and adding and subtracting from the top right position.
Step I: First Double Column
26 – 72= – 46, – 46 + 63= 17,
17 – 63= – 46, – 46 + 94= 48.
Answer is 48 → Step-I
Step II: Second Double Column:
10 – 45= – 35, – 35 + 52= 17,
17 – 27= – 10, – 10 + 82= 72.
Answer is 72 → Step-II
Now Combine the Step II and Step I.
Answer will be 7248.
You will get the same answer if you also use the normal method.
Example (2):
7676
– 1431
+5276
– 3489
+1546
_____________
Explanation: We have to look the signs given before the numbers and then start adding and adding and subtracting from the top right position.
Step I: First Double Column
76 – 31= 45, 45 + 76= 121 (here in the 121 take the last two digits from 121 i.e., 21)
21 – 89= – 68, – 68 + 46= -22 (Here the answer comes in minus so add 100 with the answer)
100 + (- 22) = 78.
Answer is 78 → Step I
Step II: Second Double Column
76 – 14= 62, 62 + 52= 114 (Take the last two digits from 114 i.e., 14)
14 – 34= – 20, – 20 + 15= – 5 (Here the answer comes in minus so add 100 with the answer)
100 + (-5) = 95
Answer is 95 → Step II.
Now Combine the Step II and Step I.
The answer will be 9578.
Shortcut Numerical Ability Rules for Basic Division
1.) DIVISIBLE BY 2:
A number will be divisible by 2, if the unit digit in the number is 0, 2, 4, 6 and 8.
Example: Numbers like, 56456, 32658, 89846 are divisible by 2.
2.) DIVISIBLE BY 4:
A number will be divisible by 4, if the last two digits of the number is divisible by 4.
Example: Numbers like 56536 is divisible by 4, because the last two digits of this number is divisible by 4 and the number 546642 is not divisible by 4 because the last two digits of this number is not divisible by 4.
3.) DIVISIBLE BY 6:
A number will be divisible by 6, if that number is divisible by both 2 and 3.
Example: 36 is divisible by 6 because 36 is divisible by both 2 and 3.
4.) DIVISIBLE BY 8: A number will be divisible by 8, if the last three digits of that number are divisible by 8.
Example: 565144 is divisible by 8 because the last three digits 144 is divisible by 8. And the number 554314 is not divisible by 8 because the last three digits 314 is not divisible by 8.
5.) DIVISIBLE BY 5:
A number will be divisible by 5 if the unit digit is either 0 or 5.
Example: Numbers like 565520 and 898935 are divisible by 5.
6.) DIVISIBLE BY 3:
A number will be divisible by 3, if the sum of the digits in the number is divisible by 3.
Example: 658452 is divisible by 3 because the sum of the numbers is divisible by 3, 6+5+8+4+5+2= 30, which is divisible by 3.
The number 456455 is not divisible by 3, because the sum of the number is not divisible by 3. 4+5+6+4+5+5= 29 this is not divisible by 29.
7.) DIVISIBLE BY 9:
A number will be divisible by 9, if the sum of the digits in the number is divisible by 9.
Example: 898686 is divisible by 9 because the sum of the numbers is divisible by 9,
8+9+8+6+8+6= 45, this is divisible by 9.
8.) DIVISIBLE BY 11:
A number will be divisible by 11, if the difference of the sum of the digits in the Odd places and Sum of the digits in the Even places, is either zero or divisible by 11.
Example: 502678 is divisible by 11 because, the sum of the digits of the odd places, 5+2+7= 14, sum of the digits in the even places, 0+6+8=14, the difference is 14-14=0, so this number is divisible by 11.
9.) DIVISIBLE BY 12:
A number is divisible by 12, if the number is divisible by both 3 and 4.
Example: 144 is divisible by 12, because it is divisible by both 3 and 4.
10.) DIVISIBLE BY 10:
Any number that ends with zero will be divisible by 10.
Dear Aspirant, Hope the above explanation of Numerical ability tricks will be more helpful to you. If you need any guidance or regarding your doubt drop your message in the comment section. Our team is onboard and ready to support you always. Find the PDF File link of Numerical Ability Tricks. It is free to download. Click, download and read it and score more in Numerical Ability topic.





