Dear Readers, SBI is conducting Online preliminary Examination for the recruitment of Clerical Cadre. preliminary Examination of SBI Clerk was scheduled from June 2018. To enrich your preparation here we have providing new series of Data Interpretation – Quantitative Aptitude Questions. Candidates those who are appearing in SBI Clerk Prelims Exams can practice these Quantitative Aptitude average questions daily and make your preparation effective.
Click “Start Quiz” to attend these Questions and view Solutions
Click here to view Quantitative Aptitude Questions in Hindi
Directions (Q. 1 – 5): Read the following information carefully and answer the following questions given below. The table below shows no of balls in different bags
| Bags
|
Red | Yellow | Blue | Green |
| A
|
4 | 7 | ||
| B
|
2 | 3 | 5 | |
| C
|
6 | 4 | 8 | 5 |
| D
|
4 | 2 | 8 | |
| E
|
2 | 4 | ||
| F
|
3 | 5 | 4 |
Note: All the questions are independent from each other
- If the probability of getting a red from bag A is 1/5 when one ball is picked random and the number of yellow balls are twice the blue balls then find the probability of getting both yellow balls when 2 balls are picked from bag A randomly?
a) 3/38
b) 3/10
c) 1/7
d) 6/11
e) None of these
- If the number of red balls in bag D is 3/4 of the yellow balls in bag C and 3 green balls are transferred from bag B to bag D then find the probability of getting at least one yellow ball from bag D when two balls are picked at random from bag D?
a) 3/38
b) 3/10
c) 7/19
d) 6/11
e) None of these
- If ‘x’ number of blue balls are added in Bag C then the probability of getting a green ball when one ball is picked at random is 1/6 then find the value of x?
a) 3
b) 10
c) 7
d) 6
e) None of these
- If the number of total balls in bag E is 16 and yellow and blue balls are in the ratio of 2:3 then find what is the probability of getting one blue ball and two green balls when three balls are picked at random?
a) 9/140
b) 3/121
c) 11/73
d) 6/117
e) None of these
- If 3 blue balls are taken out from bag F and then one ball is picked at random from bag F then the probability of getting a blue ball is 1/3 then find how many balls were there in the bag initially?
a) 8
b) 30
c) 17
d) 21
e) None of these
Directions (Q. 6 – 10): Study the following information carefully and answer the question given below.
The following table represents the number of students enrolled in six different colleges, percentage of students left the college and percentage of students who passed out the college among those who continued their study in the college.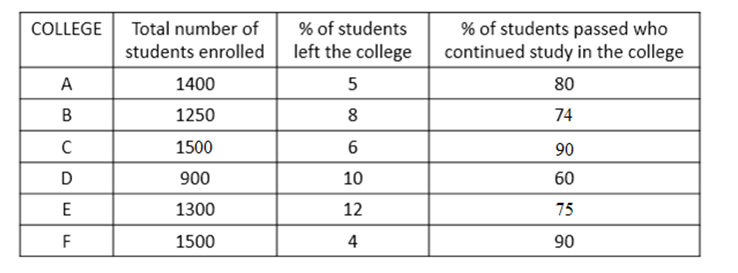
- Find the sum of total number of students from all the colleges, who continued their study.
a) 7136
b) 7120
c) 7284
d) 7350
e) None of these
- Number of students passed from college B is approximately what percent of the number of students passed from college D?
a) 152 %
b) 175 %
c) 187 %
d) 124 %
e) 168 %
- Total number of students enrolled in A and B together is approximately what percent more than the number of students enrolled in C and D together?
a) 6 %
b) 10 %
c) 14 %
d) 19 %
e) 23 %
- Find the ratio of number of failed students of college C and college F respectively.
a) 38 : 41
b) 55 : 58
c) 47 : 48
d) 32 : 43
e) None of these
- Passed students of college A is what percent of failed students of college E?
a) 161.34 %
b) 384.41%
c) 211.52%
d) 372.02 %
e) 189.65 %
Answers:
Directions (Q. 1 – 5):
- Answer (a)
Explanation:
Let the number of blue balls in the bag A be x
Yellow balls= 2x
So,
Total balls= 4+7+x+2x= 3x+11
4C1/ (3x+11)C1 = 1/5
4/(3x+11) = 1/5
3x+11= 20
3x= 20-11
3x= 9
x= 3
Blue balls= 3
Yellow balls= 6
Probability of getting two yellow balls= 6C2/20C2= 15/190 = 3/38
- Answer (c)
Explanation:
Number of red balls in bag D = 3*4/4= 3
Number of green balls in bag D= 8+3= 11
Probability of not getting a yellow ball= 16C2/20C2= 120/ 190 = 12/19
Probability of getting at least one yellow ball= 1- 12/19= 7/19
- Answer (c)
Explanation:
Total number of balls in bag C= 23
After addition= 23+x
So,
5C1/(23+x)C1= 1/6
5/(23+x) = 1/6
30= 23+x
x= 7
Number of blue balls added(x) = 7 balls
- Answer (a)
Explanation:
Number of blue and yellow balls= 16-6= 10
Number of blue balls= 2*10/5= 4
Number of yellow balls = 10- 4= 6
So,
Required probability= (6C1 * 4C2)/ 16C3 = 9/140
- Answer (d)
Explanation:
Let the number of blue balls in bag F initially be x
Balls taken out= x-3
Balls left = 3+5+4+x-3= x+9
So,
(x-3)C1/(x+9)C1 = 1/3
x-3 / x+9= 1/3
3x- 9= x+9
2x= 18
x= 9
So, number of blue balls initially = 9
Total balls in the bag initially= 9+3+4+5= 21balls
Directions (Q. 6 – 10):
- Answer (c)
Explanation:
A = (100 – 5)/100 x 1400 = 1330
B = (100 – 8)/100 x 1250 = 1150
C = (100 – 6)/100 x 1500 = 1410
D = (100 – 10)/100 x 900 = 810
E = (100 – 12)/100 x 1300 = 1144
F = (100 – 4)/100 x 1500 = 1440
Required sum = 1330 + 1150 + 1410 + 810 + 1144 + 1440 = 7284
- Answer (b)
Explanation:
Number of students who continued study in B = [(100 – 8)/100] x 1250 = 1150
Passed = (74/100) x 1150 = 851
Number of students who continued study in D = [(100 – 10)/100] x 900 = 810
Passed = (60/100) x 810 = 486
Required % = (851/486) x 100 = 175.102 % = 175 %
- Answer (b)
Explanation:
Total number of students enrolled in A and B together = 1400 + 1250 = 2650
Total number of students enrolled in C and D together = 1500 + 900 = 2400
Required percentage = [(2650 – 2400)/2400] x 100 = 10.416% = 10 %
- Answer (c)
Explanation:
Number of students who continued study in C = (100 – 6)/100 x 1500 = 1410
Failed = (100-90)/100 x 1410 = 141
Number of students who continued study in F = (100 – 4)/100 x 1500 = 1440
Failed = (100 – 90)/100 x 1440 = 144
Required ratio = 141 : 144 = 47 : 48
- Answer: (d)
Explanation:
Number of students who continued their study from college A
= (100 – 5)/100 x 1400 = 1330
Passed = 80/100 x 1330 = 1064
Number of students who continued their study from college E
= (100 – 12)/100 x 1300 = 1144
Failed = (100 – 75)/100 x 1144 = 286
Required % = (1064/286) x 100 = 372.02 %
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Logical Reasoning | 10.00 AM |
| Quantitative Aptitude “20-20” | 11.00 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| Static GK Quiz | 1.00 PM |
| English Language “20-20” | 2.00 PM |
| Banking Awareness Quiz | 3.00 PM |
| Reasoning Puzzles & Seating | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| Data Interpretation / Application Sums (Topic Wise) | 6.00 PM |
| Reasoning Ability “20-20” | 7.00 PM |
| English Language (New Pattern Questions) | 8.00 PM |
| General / Financial Awareness Quiz | 9.00 PM |
Click Here for More Quantitative Aptitude Questions





