Dear Readers, SBI is conducting Online Examination for the recruitment of probationary officer. To enrich your preparation here we have providing new series of Data Interpretation – Quantitative Aptitude Questions. Candidates those who are appearing in SBI PO Mains Exams can practice these Quantitative Aptitude average questions daily and make your preparation effective.
Click “Start Quiz” to attend these Questions and view Solutions
Click here to view Quantitative Aptitude Questions in Hindi
Directions (1-5): Study the following graph carefully and answer the questions.
The graph below shows a no. of days taken by 5 people A, B, C, D and E to complete a work and no. of days for which they worked.
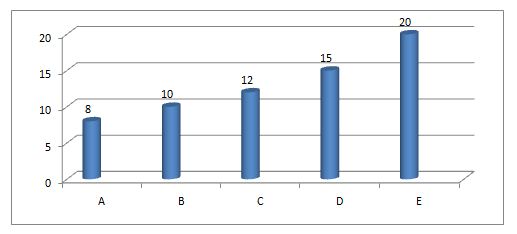
| Persons | No. of days for which person worked |
| A | 2 |
| B | – |
| C | 1 |
| D | – |
| E | 4 |
1) To complete the given work A worked for 4 days, C worked for 1 day and remaining work was completed by P and Q. The ratio of days in which P and Q worked was 2:3. Also P alone can complete the work in 24 days and Q in 9 days. How many no. of days in which all A, C, P and Q completed the work?
a) 10
b) 20
c) 30
d) 15
e) 16
2) After all worked for given no. of days and completed 14/15th of the total work. B worked for 1 day less than D. How many days did B work?
a) 1
b) 2
c) 3
d) 4
e) 1.5
3) Efficiency of S is twice that of A and that of T is thrice that of C. D worked for 3 days, after which he was replaced by S and T. Now they completed the remaining work. Find the total no. of days taken to complete the work.
a) 27/5
b) 20/7
c) 30/7
d) 15/4
e) 23/5
4) B worked for 5 days at half of his original efficiency and then for 5 days at his full efficiency. The remaining work was completed by E. Find the total no. of days taken to complete the work.
a) 14
b) 15
c) 17
d) 20
e) 25
5) Person P takes double the time of what B and D together take to do the work. Efficiency of P is twice of that of Q.Q worked for 4 days, P worked for 6 days. For how many days should C work to complete the remaining work?
a) 2
b) 3
c) 4
d) 6
e) 7
Directions (6-10): Study the following graph and answer the given questions.
The line graph shows the speed of the stream
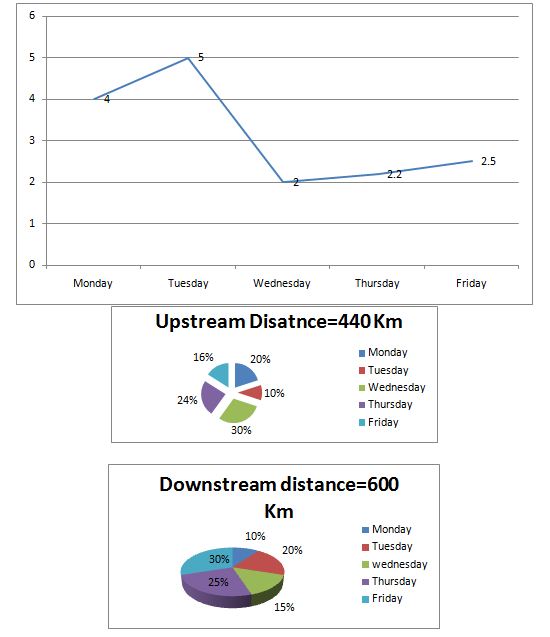
6) The speed of the boat on Monday in still water is 125% of the speed of the boat on Wednesday in still water. If the speed of the boat on Wednesday is 16 km/hr, then what will be the ratio of the time taken by the boat on Monday to travel upstream to the time taken by the boat on Wednesday to travel downstream?
a) 29:67
b) 55:83
c) 38:53
d) 27:82
e) None of these
7) If the ratio of the speed of boat on Tuesday in still water to the speed of boat Thursday in still water is 4:5, then what will be the approximate average time taken by boat on Thursday to travel upstream and downstream together if the speed of boat on Tuesday in still water is 20 km/hr?
a) 10hours
b) 6hours
c) 2hours
d) 8hours
e) 5 hours
8) Time taken by the boat to cover the upstream distance on Monday is same as time taken by the boat to cover the downstream distance on Tuesday. If total speed of the boat in still water on Monday and Tuesday is 25km/hr, then find the ratio of the speed of still water on Monday and Tuesday.
a) 1:4
b) 2:5
c) 3:2
d) 3:5
e) 5:3
9) On Wednesday, the boat takes a total time 10 hr 30 minutes to cover both upstream and downstream distance. If the ratio of speed of boat in still water is going upstream and downstream is 4:3 then find the speed of boat in still water while going downstream.
a) 24km/hr
b) 18km/hr
c) 17km/hr
d) 15km/hr
e) 7km/hr
10) The time taken by the boat on Friday to travel downstream is 1 hour more than the time taken by the boat to travel upstream on Thursday. Find the approximate total time taken by the boat in still water on Thursday to travel the distance equivalent to the distance covered by the boat on Thursday in downstream if the speed of the boat on Friday in still water is 3.5 km/hr.
a) 24hrs 32 mins
b) 23 hrs 20 mins
c) 36 hrs 24 mins
d) 34 hrs 40 mins
e) 25 hrs 40 mins
Answers:
1). Answer: a)
A’s total work =8 days
A worked for 4 days=4/8
C’s total work =12days
C worked for 1 day=1/12
A and C completed= 4/8 + 1/12=7/12 work
So P and Q completed 1-7/12=5/12 work
Days=2x and 3x
So 2x/24+3x/9=5/12.
By solving, x=1
So total days=4+1+2+3=10 days.
2). Answer: b)
A+B+C+D+E=14/15th of work (remaining work 1/15 given)
So 2/8+(D-1)/10+1/12+D/15+4/20=14/15(efficiency/time taken)
B=D-1(as per given data)
(15+6D-6+5+4D+12)=56
10D= 30
D=3(By solving)
So B worked for 2 days
3). Answer: e)
A can complete the work in 8 days, so S in 8/2=4 days.
C can complete the work in 12days, so S in 12/3=4 days.
D worked for 3 days, so did 3/15=1/5 of work.
So remaining work=4/5
Now S and T worked for same no. of days=X
So (1/4+1/4)*x=4/5
By solving, we get x=8/5 days
So total 3+8/5=23/5 days
4). Answer: b)
At half of his efficiency B will take 20 days to complete the work
B worked for 5 days=5/20(half efficiency)
B worked for 5 days=5/10(full efficiency)
Remaining work by E=x/12
So 5/20+5/10+x/20=1
5+10+x=20
X=20-15=5 days
Hence total days=5+5+5=15 days
5). Answer: c)
B and D together take 6 days. So P takes 12 days and Q takes 24 days.
P+Q+C=4/24+6/12+C/12=1
C=4
Direction (6-10)
6). Answer: e)
Given that speed of the boat in still water on Wednesday= 16kmph
Also speed of the boat in still water on Monday= 16*125/100=20 kmph
We know that speed= Distance/time
Also upstream speed= x-y and downstream speed= x + y
Then upstream time of the boat on Monday= (20*440) / (100*(20-4)) =5.5
Downstream time of the boat on Wednesday= (15*600) / (100*(16+2)) =5
Required ratio= 5.5:5=11:10
7). Answer: e)
Let the speed of boat on Tuesday in still water be 4x and speed of boat on Thursday in still water be 5x.
Then given that 4x= 20
x= 5 km/hr
Then the speed of boat Thursday in still water=5*5=25km/hr
Now, time taken by the boat to travel upstream on Thursday= (24*440)/ (100*22.8) = 4.5 hours (approximately)
And time taken by the boat to travel downstream on Thursday=(25*600)/(100*27.2) =5.5 hours (approximately)
Required average= (4.5+5.5)/2= 5 hours
8). Answer: c)
Let x be the speed of the boat in still water on Monday and y be the speed of the boat in still water on Tuesday.
We know that Time=Distance/Speed
Also given that, x + y=25
Then y= 25-x
Now, 88/(x-4) =120/(y+5)
88/(x-4) =120/ (25-x+5)
11/(x-4)=15/(30-x)
11(30-x) = 15(x-4)
330-11x = 15x-60
390 = 26x
x= 15 km/hr
Then y= 10 km/hr
Required ratio=15:10=3:2
9). Answer: b)
Let speed of boat in still water is going in upstream= 4x
And speed of boat in still water is going in downstream=3x
We know that, Time= Distance/speed
Then [132/(4x-2)]+90/(3x+2)]=10(1/2)
After solving we get x= 6 km/hr.
Then 3x= 18 km/hr
10). Answer: e)
Given that, the speed of the boat in still water= 3.5 km/hr
Now, time taken by the boat on Friday to travel Downstream= (30*600)/(100*(3.5+2.5))
= 30 hours
Then time taken by the boat on Thursday to travel upstream= 30-1=29 hours
Upstream speed of the boat on Thursday= (24*440)/(100*29)= 3.64 km/hr
Then speed of the boat in still water on Thursday= 3.64+2.2=5.84 km/hr
And downstream speed of the boat on Thursday= 5.84+2.2= 8.04 km/hr
Thus time taken by the boat on Thursday in still water= (25*600)/(100*5.84) = 25 hours 40 minutes (approximately)
Daily Practice Test Schedule | Good Luck
| Topic | Daily Publishing Time |
| Daily News Papers & Editorials | 8.00 AM |
| Current Affairs Quiz | 9.00 AM |
| Quantitative Aptitude “20-20” | 11.00 AM |
| Vocabulary (Based on The Hindu) | 12.00 PM |
| General Awareness “20-20” | 1.00 PM |
| English Language “20-20” | 2.00 PM |
| Reasoning Puzzles & Seating | 4.00 PM |
| Daily Current Affairs Updates | 5.00 PM |
| Data Interpretation / Application Sums (Topic Wise) | 6.00 PM |
| Reasoning Ability “20-20” | 7.00 PM |
| English Language (New Pattern Questions) | 8.00 PM |
Click Here for More Quantitative Aptitude Questions





