Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for LIC AAO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 5683]Click Here to Take LIC AAO Prelims Mock Test
Click Here for Mains 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): The following questions are accompanied by three statements I, II and III. You have to determine which statement is/are sufficient to answer the questions.
1) A and B together can complete the work in how many days?
I) A alone can complete the work in 12 days.
II) B alone can complete the work in 18 days.
III) A and B together can complete (5/6)th of the work in 6 days.
a) Both I and II alone are sufficient
b) If Either III alone or both I and II are sufficient
c) Either I or III are sufficient
d) Both I and III are sufficient
e) All three are sufficient
2) Find the perimeter of square, whose side is 4 meter less than the length of the rectangle?
I) The ratio between the length to that of breadth of the rectangle is 3: 2.
II) The perimeter of the rectangle is 80 meter.
III) The area of the rectangle is 384 Sq meter.
a) Both I and II are sufficient
b) Both I and III are sufficient
c) Any two of the given statement are sufficient
d) All three statements are sufficient
e) Either I and II or I and III are sufficient
3) Find the present age of Sanu?
I) 5 years ago, the ratio of age of Kathir and Sanu is 3: 2.
II) After 7 years, the ratio of age of Kathir and Sanu will be 21: 16.
III) The difference between the age of Kathir and Sanu is 10 years.
a) Both I and II are sufficient
b) Both I and III are sufficient
c) All three statements are sufficient
d) Any two of the given statement are sufficient
e) Either I and II or I and III are sufficient
4) Find the speed of train B (in km/hr)?
I) Train A crosses 150 m long train B running in opposite directions in 18 sec.
II) The speed of train A is 50 km/hr.
III) The length of train A is twice that of train B
a) Both I and II alone are sufficient
b) If Either III alone or both I and II are sufficient
c) Either I or III are sufficient
d) Any two of the given statement are sufficient
e) All three are sufficient
5) What is speed of the boat in still water?
I) The boat takes 6 hours to travel 48 km downstream
II) The boat takes 2 hours more to travel same distance upstream.
III) The ratio of speed of boat in still water to that of stream is 7: 1.
a) Either I and II or I and III are sufficient
b) Both I and II are sufficient
c) Both II and III are sufficient
d) All three statements are sufficient
e) Both I and III are sufficient
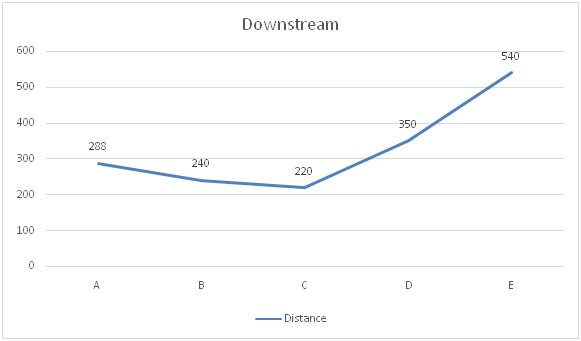
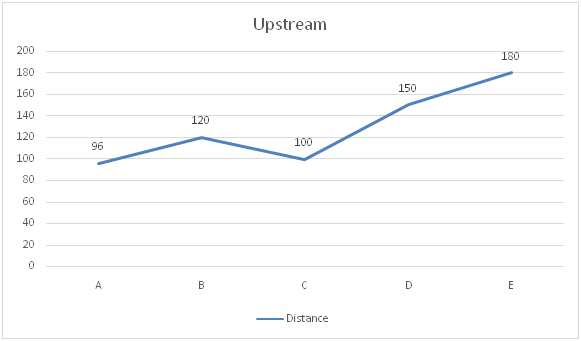
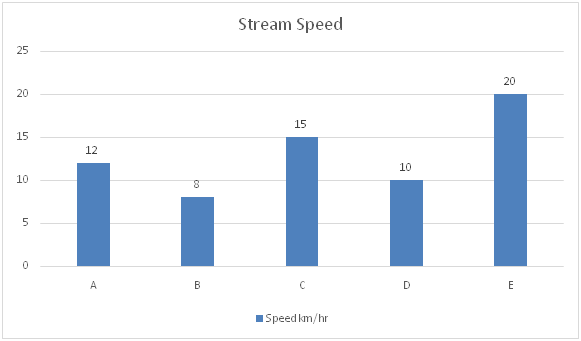
Directions (6 – 10): The two-line graph shows the distance travelled by the five different boats with the stream and against the stream in same time and the bar chart shows speed of stream.
6) Find out the speed of Boat B & D together in still water is approximately how much percentage more/less than that of speed of stream of the same boats together?
a) 70 %
b) 170%
c) 60%
d) 68%
e) 150%
7) It is known that ratio of the speed of the Boat B to Boat F in the still water is 4:5. If it’s given that Boat F travels 126 km distance with the stream, and 81 km against the stream in 7 hr 30 min, what is the speed of stream for Boat F?
a) 14
b) 13
c) 15
d) 12
e) 18
8) It’s known that distance between the two-point M & N is 210 km. Boat E travels from point M to N and Comes back. What is the time taken by Boat E in travelling total distance?
a) 12
b) 14
c) 18
d) 17
e) 16
9) Captain of the Boat thought of increasing the speed of Boat C and so in still water speed of boat is increased by 10% and stream also started flowing fast, increasing its speed by 20% due to wind. Find the time taken by the Boat C to cover 91km distance against the stream.
a) 7
b) 8.5
c) 3.5
d) 6.2
e) None of these
10) Find the ratio of the speed of Boats A and B together in still water to the speed of Boats D and E together in still water.
a) 48:55
b) 48:65
c) 43:33
d) 46:34
e) 44:34
Answers :
Direction (1-5) :
1) Answer: b)
From I and II,
A’s one day work = 1/12
B’s one day work = 1/18
(A + B)’s one day work = (1/12) + (1/18) = 30/(12*18) = 5/36
(A + B)’s one day work = 36/5 = 7 (1/5) days
Both I and II are sufficient to answer the question.
From III,
A and B together can complete (5/6)th of the work = 6 days
(5/6)*Work = 6
(A + B) can complete the work in, 6*(6/5) = 36/5 = 7 (1/5) days
Statement III alone are sufficient to answer the question.
So, Either III alone or both I and II are sufficient
2) Answer: c)
From I and II,
The ratio between the length to that of breadth of the rectangle = 3: 2 (3x, 2x)
The perimeter of the rectangle = 80 meter
2*(3x + 2x) = 80
5x = 40
X = 8
Length = 3x = 24 m
Side of square (a) = 20 m
Perimeter of square = 4a = 80 m
Both I and II are sufficient to answer the question.
From I and III,
The ratio between the length to that of breadth of the rectangle = 3: 2 (3x, 2x)
The area of the rectangle = 384 Sq meter
3x*2x = 384
6x2 = 384
X2 = 384/6 = 64
X = 8
Length = 3x = 24 m
Side of square (a) = 20 m
Perimeter of square = 4a = 80 m
Both I and III are sufficient to answer the question.
From II and III,
The perimeter of the rectangle = 80 meter
2*(l + b) = 80
= > l+ b = 40
= > b = 40 – l
The area of the rectangle = 384 Sq meter
= > lb = 384
= > l*(40 – l) = 384
40l – l2 = 384
L2 – 40l + 384 = 0
(l – 24) (l – 16) = 0
L = 24, 16
If l = 24, then b = 40 – 24 = 16
If l = 16, then b = 40 – 16 = 24
The length of rectangle is always greater than breadth. So,
L = 24, b = 16
Side of square (a) = 20 m
Perimeter of square = 4a = 80 m
Both II and III are sufficient to answer the question.
Hence, any of the three statements are necessary to answer the given question.
3) Answer: d)
From I and II,
(3x + 12) / (2x + 12) = 21/16
48x + 192 = 42x + 252
6x = 60
= > x = 10
Present age of Sanu = 2x + 5 = 25 years
Both I and II are sufficient to answer the question.
From I and III,
5 years ago, Kathir: Sanu = 3: 2
3x – 2x = 10
= > x = 10
Present age of Sanu = 2x + 5 = 25 years
Both I and III are sufficient to answer the question.
From II and III,
After 7 years, Kathir: Sanu = 21: 16
21x – 16x = 10
5x = 10
= > x = 2
Present age of Sanu = 16x – 7 = 32 – 7 = 25 years
Both II and III are sufficient to answer the question.
Hence, any of the three statements are necessary to answer the given question.
4) Answer: e)
From I, II and III,
Length of train A = 2*150 = 300 m
According to the question,
(300 + 150)/[(50 + x)*(5/18)] = 18
(450*18)/[(50 + x)*5] = 18
90 = 50 + x
X = 40 Km/hr
Hence, all three statements are required to answer the question.
5) Answer: a)
From I and II,
Speed of downstream = 48/6 = 8 km/hr
Speed of upstream = 48/8 = 6 km/hr
Speed of boat in still water = (1/2)*14 = 7 km/hr
Both I and II are sufficient to answer the question.
From I and III,
Speed of downstream = 48/6 = 8 km/hr
8x = 8
X = 1
Speed of boat in still water = 7x = 7 km/hr
Both I and III are sufficient to answer the question.
Hence, either I and II or I and III are sufficient to answer the given questions.
Directions (6 – 10):
Boat A:
Let us take speed of boat A in still water be x kmph
Given,
288/(x+12) = 96/(x-12)
3/(x+12) = 1/(x-12)
3x-36 = x+12
2x = 48 => x= 24 kmph
Speed of boat A in still water is 24 kmph
Boat B:
Let us take speed of boat B in still water be x kmph
Given,
240/(x+8) = 120/(x-8)
2/(x+8) = 1/(x-8)
X+8 = 2x-16=> x= 24 kmph
Speed of boat B in still water is 24 kmph
Boat C:
Let us take speed of boat C in still water be x kmph
Given,
220/(x+15) = 100/(x-15)
11/(x+15) = 5/(x-15)
11x-165 = 5x+75
6x = 240 => x= 40 kmph
Speed of boat C in still water is 40 kmph
Boat D:
Let us take speed of boat D in still water be x kmph
Given,
350/(x+10) = 150/(x-10)
7/(x+10) = 3/(x-10)
7x-70 = 3x+30
4x = 100 => x= 25 kmph
Speed of boat C in still water is 25 kmph
Boat E:
Let us take speed of boat E in still water be x kmph
Given,
540/(x+20) = 180/(x-20)
3/(x+20) = 1/(x-20)
3x-60 = x+20
2x = 80 => x= 40 kmph
6) Answer: b)
Speed of Boat B and D, in still water together = (24 + 25) = 49 km/h
Speed of stream of Boat B and D together = 18 km/h
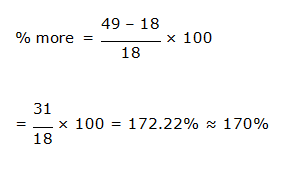
7) Answer: d)

2 (3780 – 126x + 2430 + 81x) = 15 (900 – x2)
2 (6210 – 45x) = 13500 – 15x2
12420 – 90x = 13500 – 15x2
15x2 – 90x – 1080 = 0
x2 – 6x – 72 = 0
x2 – 12x + 6x – 72 = 0
x (x – 12) + 6 (x – 12) = 0
(x + 6) (x – 12) = 0
x = –6, 12
Speed of stream = 12 km/h
8) Answer: b)
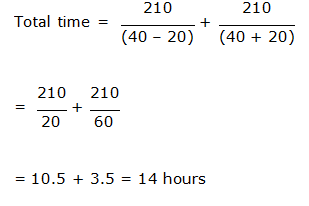
9) Answer: c)
Speed of Boat C in still water = 40 × 110% = 44 km/h
Speed of stream = 15 × 120% = 18 km/h
Time taken by Boat C to cover the distance of 91 km upstream = 91/ (44 – 18)
= 91/ 26 = 3.5 hours
10) Answer: b)
Ratio = (24 + 24) : (25 + 40)
= 48 : 65





