Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS Clerk Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
[WpProQuiz 7503]
Data sufficiency
Directions (1 – 5): In each of the following questions, a question is followed by three statements I, II and III. Read all the statements to find the answer to given question and then answer accordingly that which statement/s can give the answer alone/together.
1) Find the probability of drawing three balls of different colours from the bag.
I. The bag contains only three different coloured balls viz. red, white and blue.
II. Probability of drawing one red ball from the bag is ¼.
III. Probability of drawing one blue ball from the bag is 1/3.
a) All I, II and III
b) Any two of the three
c) Only I and III
d) Any one of the three
e) Even I, II and III together are not sufficient.
2) Find the difference between the compound interest and simple interest on that sum after two years at the rate of r% per annum.
I. The sum amounts to Rs.44100 on compound interest at 5% per annum after two years.
II. Simple interest on Rs.25000 at r% per annum after four years will be Rs.8000.
III. The sum amounts to Rs.59200at 8% per annum after six years.
a) All I, II and III
b) Any two of the three
c) Only II and III
d) Only II and either I or III
e) Even I, II and III together are not sufficient.
3) If 42x÷ 412 x 64 ÷ 4y x 16 = 1024, find 2xy.
I. x > 0 and y > 0
II. x – y = 5
III. x + y = 9
a) All I, II and III
b) Any two of the three
c) Either II or III
d) Only II and either I or III
e) Even I, II and III together are not sufficient.
4) Is 1/(x – 2y) a natural number?
I. x > 0, y > 0
II. x> y
III. 2x – y = 6
a) All I, II and III
b) Any two of the three
c) Only II and III
d) Only II and either I or III
e) Even I, II and III together are not sufficient.
5) Urmila, Tina and Jaya entered into a partnership for three years. Find the share of Urmila in the profit.
I. Urmila, Tina and Jaya invested in the ratio 8:4:5. After one year Tina doubled her investment.
II. At the end of three years, they earned a total profit of Rs.80000.
III. After two years, Jaya doubled her investment.
a) All I, II and III
b) Any two of the three
c) Either II or III
d) Only II and either I or III
e) Even I, II and III together are not sufficient.
Data Interpretation
Directions (Q. 6 – 10) Study the following information carefully and answer the given questions:
The following table shows the total number of mails received in inbox by different users and the percentage of mails read by the users and the total number of spam mails received in a month.
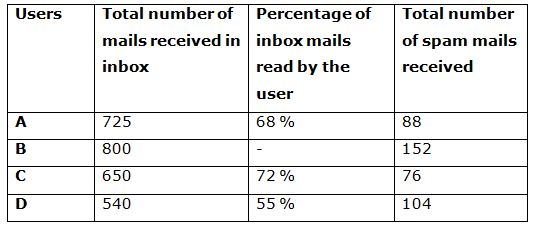
Note:
The spam mails didn’t read by the user.
The total number of mails received = Total mails received in Inbox + Total number of spam mails received.
“-“ indicates that you have to find the answer according to the question they asked.
6) Find the difference between the total number of mails didn’t read by the user A to that of user C?
a) 56
b) 43
c) 62
d) 69
e) None of these
7) Number of mails read is what percentage of the total mails received in inbox by the user B, if total number of spam mails received by the user B is 38 % of total mails didn’t read by the user?
a) 35 %
b) 65 %
c) 80 %
d) 50 %
e) None of these
8) Find the total number of mails read by all the given user, if the percentage of mails read by the user B is 66 %?
a) 2154
b) 1786
c) 2378
d) 1921
e) None of these
9) Find the ratio between the total number of mails didn’t read by the user C to that of total number of spam mails received by the user D?
a) 129: 52
b) 153: 31
c) 166: 23
d) 140: 11
e) None of these
10) The total number of mails received in Inbox by the user D is approximately what percentage of total number of spam mails received by user A and C together?
a) 400 %
b) 370 %
c) 330 %
d) 260 %
e) 240 %
Answers:
Directions (1-5):
1) Answer: e)
Let, red = x
White = y
Blue = z
From I:
The bag contains only three different coloured balls viz. red, white and blue.
From II:
Probability of drawing one red ball from the bag is ¼.
From III:
Probability of drawing one blue ball from the bag is 1/3.
From I, II and III:
x/(x + y + z) = ¼
=> 4x = x + y + z
=> 3x – y – z = 0
And
z/(x + y + z) = 1/3
=> 3z = x + y + z
=> x + y – 2z = 0
Since, there are three variables, we need three equations to solve the question.
Hence, even I, II and III together are not sufficient.
2) Answer: d)
From I and II:
We know that
Amount on CI = P x (1 + r/100)t
=> 44100 = P x (1 + 5/100)2
=> 44100 = P x 105/100 x 105/100
=> P = 44100 x 100/105 x 100/105
=> P = Rs.40000
And
We know that
SI = (P x r x t)/100
8000 = (25000 x r x 4)/100
=> 8000 = 1000 x r
=> r = 8%
We know that, for two years
CI – SI = P x (r/100)2
= 40000 x (8/100)2
= 40000 x (2/25)2
= 40000 x 4/625
= Rs.256
From II and III:
We know that
SI = (P x r x t)/100
8000 = (25000 x r x 4)/100
=> 8000 = 1000 x r
=> r = 8%
And
Amount on SI = (P x r x t)/100 + P
=> 59200 = (P x 8 x 6)100 + P
=> 59200 = 48P/100 + P
=> 59200 = (48P + 100P)/100
=> 59200 = 148P/100
=> P = 592000 x 100/148
=> P = Rs.40000
We know that, for two years
CI – SI = P x (r/100)2
= 40000 x (8/100)2
= 40000 x (2/25)2
= 40000 x 4/625
= Rs.256
Hence, Only II and either I or III are sufficient.
3) Answer: c)
42x÷ 412 x 64 ÷ 4y x 16 = 1024
=>42x÷ 412 x 43÷ 4y x 42 = 45
=> 4(2x – 12 + 3 – y + 2) = 45
=> 2x – 12 + 3 – y + 2 = 5
=> 2x – y = 5 + 7
=> 2x – y = 12 —— (i)
From I:
x> 0 and y > 0
From II:
x – y = 5 ——- (ii)
Subtracting (ii) from (i)
2x – y – x + y = 12 – 5
=> x = 7
From (ii)
7 – y = 5
=> y = 2
Now, 2xy = 2 x 7 x 5 = 70
From III:
x + y = 9 ——- (iii)
Adding (i) and (iii)
2x – y + x + y = 12 + 9
=> 3x = 21
=> x = 7
From (iii)
7 + y = 9
=> y = 2
Now, 2xy = 2 x 7 x 5 = 70
Hence, either II or III is sufficient.
4) Answer: e)
From I:
x> 0, y > 0
From II:
x > y
From III:
2x – y = 6
From I, II and III:
x> 0, y > 0
x > y
2x – y = 6
By hit and trial
x = 4, y = 2
1/(4 – 2 x 2) = 1/0 = (cannot defined)
But, since we have one equation, value of x and y cannot be determined and hence, required answer cannot be determined.
Hence, Even I, II and III together are not sufficient.
5) Answer: a)
From I:
Urmila, Tina and Jaya invested in the ratio 8:4:5. After one year Tina doubled her investment.
From II:
At the end of three years, they earned a total profit of Rs.80000.
From III:
After two years, Jaya doubled her investment.
From I, II and III:
Let, amounts invested by Urmila, Tina and Jaya be Rs.8k, Rs.4k and Rs.5k respectively.
Ratio of share in the profit:
Urmila : Tina : Jaya = (8k x 3) : (4k + 8k x 2) : (5k x 2 : 10k)
= 24k : 20k : 20k
= 6 : 5 : 5
Share of Urmila in the profit = 6/(6 + 5 + 5) x 80000
= 6/16 x 80000
= Rs.30000
Hence, all I, II and III together are sufficient.
Directions (6-10):
6) Answer: c)
The total number of mails didn’t read by the user A
= > 725*(32/100) + 88
= > 232 + 88 = 320
The total number of mails didn’t read by the user C
= > 650*(28/100) + 76
= > 182 + 76 = 258
Required difference = 320 – 258 = 62
7) Answer: d)
The total number of spam mails received by the user B = 38 % of total mails didn’t read by the user
152 = (38/100)* total mails didn’t read by the user
Total mails didn’t read by the user B = 15200/38 = 400
Total mails read by the user B = 800 – 400 = 400
The percentage of mails read by the user B
= > (400/800)*100 = 50 %
8) Answer: b)
The percentage of mails read by the user B = 66 %
The total number of mails read by all the given user
= > 725*(68/100) + 800*(66/100) + 650*(72/100) + 540*(55/100)
= > 493 + 528 + 468 + 297 = 1786
9) Answer: a)
The total number of mails didn’t read by the user C
= > 650*(28/100) + 76= 258
The total number of spam mails received by the user D = 104
Required ratio = 258: 104 = 129: 52
10) Answer: c)
The total number of mails received in Inbox of user D = 540
The total number of spam mails received by user A and C together
= > 88 + 76 = 164
Required % = (540/164)*100 = 330 %





