Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7288]
Data interpretation
Direction (1 – 5): Study the following data carefully and answer the questions:
Line graph given below shows the speed (km/h) of five different boats in still water:
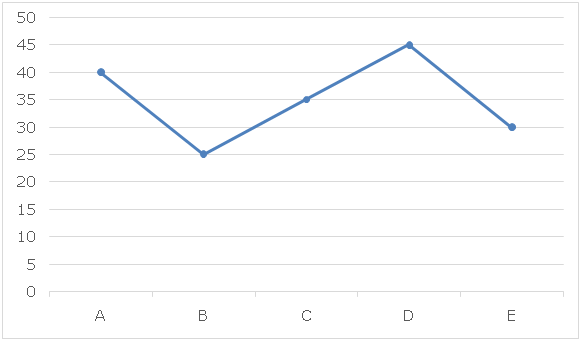
Table given below shows the speed (km/h) of stream on five different days of a week:
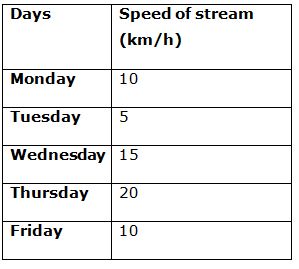
Note: Speed of any boat will remain same on all the five different days.
1) On Monday, boat C goes ‘D’ km upstream and comes back to the same point in 4.2 hours, then what is the time taken by boat B to go ‘D + 12.5’ km in upstream on Wednesday?
a) 10 hours
b) 8 hours
c) 12 hours
d) 6 hours
e) None of these
2) If time taken by boat A to cover ‘D + 15’ km in upstream on Tuesday is same as the time taken by boat C to cover ‘2D’ km in downstream on Thursday, then what is the total time taken by boat D on Tuesday to go ‘D’ km upstream and comes back to the original point?
a) 215 hours
b) 475 hours
c) 265 hours
d) 385 hours
e) None of these
3) Distance travelled by boat A on Friday in downstream in ‘2t’ hours is same as the distance travelled by boat B on Thursday in upstream in ‘t + 11.4’ hours, then what is the total distance travelled by boat C on Monday in upstream in ‘t + 1.2’ hours?
a) 40 km
b) 30 km
c) 50 km
d) 45 km
e) None of these
4) If time taken by boat E on Monday to cover ‘D’ km in upstream is 1 hour more than the time taken by same boat to cover ‘D’ km in downstream on Wednesday, then on Tuesday by what percent boat B should reduces its speed of stream so that it take 36 minutes more to cover ‘D’ km in upstream than time taken by it to cover ‘D’ km in upstream with its original speed of stream?
a) 20%
b) 25%
c) 10%
d) 30%
e) None of these
5) If ratio of time taken by boat C (when speed of the boat in still water reduces to 80%) to cover ‘D’ km in downstream on Tuesday to time taken by boat D (when speed of boat in still water is increased by 20%) to cover ‘D + 12’ km in upstream on Wednesday is 10: 11, then what is the value of ‘D’?
a) 50
b) 60
c) 40
d) 30
e) None of these
Data Interpretation
Direction (6 – 10): Study the following data carefully and answer the questions:
Fare of cab is calculated on the basis on fuel charge, distance covered (km) and time taken (hours) in the journey. Formula to calculate fare of the cab is given below:
Fare of the cab = Fuel charges + 10 * Distance covered + 20 * Time taken – Rebate
Fuel charges = 160% of (Distance covered * Time taken)
Pie charts given below shows the distribution (degree) of total distance covered (km) and per cent distribution of speed (km/h) of the cab for five different persons P, Q, R, S and T respectively.
Sum of the first pie chart and second pie chart is 90 km and 200 km/h respectively.
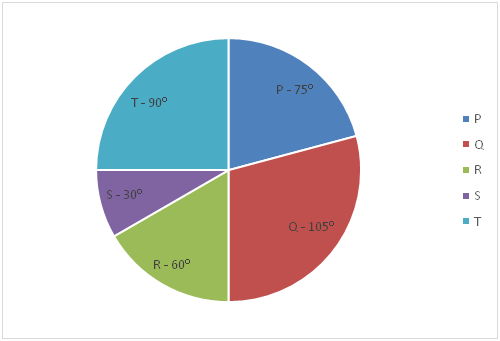

6) If Rebate on the fare of the cab for person P is calculated based on the following given formula, then what will be the total fare of the cab for person P?
Rebate = 2 * (Fuel charges * Time taken)
a) Rs.256.25
b) Rs.262.75
c) Rs.246.5
d) Rs.272.5
e) None of these
7) If formula to calculate Rebate on the fare of cab for person Q is given below and total fare of cab for him is Rs.350, then what is the total amount of toll tax is paid by person Q?
Rebate = (75% of toll tax + Rs.16)
a) Rs.90
b) Rs.80
c) Rs.120
d) Rs.100
e) None of these
8) If Rebate on the fare of cab for person R is ‘x – 5.2’ and total amount of fare of cab for him is ‘x2 + 16’, then what is the difference between fuel charges and rebate on the fare of cab for person R?
a) Rs.10
b) Rs.8
c) Rs.12
d) Rs.4
e) None of these
9) If amount of Rebate for person S for his fare of cab is ‘x2 + 3x – 6’ and total amount of fare paid by him is Rs.102.4, then which of the following is correct fuel charges of cab for person S?
a) (2x – 0.4)
b) 2x
c) (2x + 0.4)
d) (x + 0.4)
e) None of these
10) If Rebate on the cab fare for person T is calculated as given below, then what will be the total amount of fare for cab is paid by person T?
Rebate = 60% of Distance covered + 125% of fuel charges
a) Rs.292.2
b) Rs.286.8
c) Rs.272.4
d) Rs.280.6
e) None of these
Answers :
Directions (1-5) :
1) Answer: b)
According to the question:
[D/(35 – 10)] + [D/(35 + 10)] = 4.2(D/25) + (D/45) = 4.2
9D + 5D = 4.2 * 225
14D = 945
D = 67.5
Total time taken by boat B on Wednesday to cover ‘D + 12.5’ km in upstream
= [(67.5 + 12.5)/(25 – 15)] = 80/10 = 8 hours
2) Answer: b)
According to the question:
[(D + 15)/(40 – 5)] = [2D/(35 + 20)](D + 15)/35 = 2D/55
11(D + 15) = 7 * 2D
11D + 165 = 14D
3D = 165
D = 55
Total time taken by boat D on Tuesday to go ‘D’ km upstream and comes back to the original point = [55/(45 – 5)] + [55/(45 + 5)] = (55/40) + (55/50)
= 1.375 + 1.1 = 2.475 hours
3) Answer: d)
According to the question:
2t * (40 + 10) = (t + 11.4) * (25 – 20)
100t = 5t + 57
95t = 57
t = 0.6
Total distance travelled by boat C on Monday in upstream in ‘t + 1.2’ hours
= (0.6 + 1.2) * (35 – 10) = 45 km
4) Answer: a)
According to the question:
(30 – 10) * (t + 1) = (30 + 15) * t
20t + 20 = 45t
25t = 20
t = 0.8
D = (30 + 15) * t = 36 km
Actual time taken by boat B to cover 36 km in upstream on Tuesday
= 36/(25 – 5) = 1.8 hours
Let decreased speed of boat B in still water = ‘x’ km/h
According to the question:
36/(x – 5) = 1.8 + (36/60)
36/(x – 5) = 2.4
36 = 2.4x – 12
2.4x = 48
x = 20
Required percent = [(25 – 20)/25] * 100 = 20%
5) Answer: c)
Changed downstream speed of boat C on Tuesday = (80% of 35) + 5
= 28 + 5 = 33 km/h
Changed upstream speed of boat D on Wednesday = (120% of 45) –15
= 54 – 15 = 39 km/h
According to the question:
[D/33]: [(D + 12)/39] = 10: 1139D/33(D + 12) = 10/11
39D = 30D + 360
9D = 360
D = 40
Directions (6 – 10):
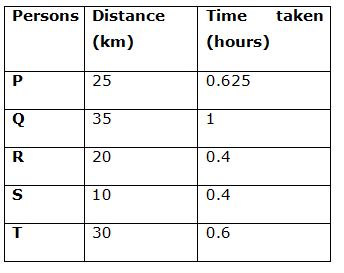
Distance covered by P = 120 * (75/360) = 25 km
Speed of person P = 20% of 200 = 40 km/h
Time taken by person P = 25/40 = 0.625 hours
Distance covered by Q = 120 * (105/360) = 35 km
Speed of person Q = 17.5% of 200 = 35 km/h
Time taken by person Q = 35/35 = 1 hour
Distance covered by R = 120 * (60/360) = 20 km
Speed of person R = 25% of 200 = 50 km/h
Time taken by person R = 20/50 = 0.4 hours
Distance covered by S = 120 * (30/360) = 10 km
Speed of person S = 12.5% of 200 = 25 km/h
Time taken by person S = 10/25 = 0.4 hours
Distance covered by T = 120 * (90/360) = 30 km
Speed of person T = 25% of 200 = 50 km/h
Time taken by person T = 30/50 = 0.6 hours
6) Answer: a)
Fuel charges = 160% of 25 * 0.625 = Rs.25
Rebate = 2 * (25 * 0.625) = Rs.31.25
Total fare = 25 + 10 * 25 + 20 * 0.625 – 31.25
= 25 + 250 + 12.5 – 31.25
= Rs.256.25
7) Answer: b)
Fuel charge = 160% of (35 * 1) = Rs.56
Let amount of toll tax = ‘x’
Rebate = (75% of x + 16) = (0.75x + 16)
Total fare = 56 + 10 * 35 + 20 * 1 – (0.75x + 16) = 350
56 + 350 + 20 – 350 – 16 = 0.75x
0.75x = 60
x = 80
Total amount of toll tax paid = Rs.80
8) Answer: d)
Fuel charges = 160% of (20 * 0.4) = Rs.12.8
Rebate = (x – 5.6)
Total fare = 12.8 + 10 * 20 + 20 * 0.4 – (x – 5.6) = (x2 + 16)
220.8 – x + 5.2 = x2 + 16
x2 + x – 210 = 0
x = 14 and -15
Rebate on cab fare = x – 5.2 = Rs.8.8
Required difference = 12.8 – 8.8 = Rs.4
9) Answer: c)
Fuel charges = 160% of (10 * 0.4) = Rs.6.4
Rebate = x2 + 3x – 18
Total fare = 6.4 + 10 * 10 + 20 * 0.4 – (x2 + 3x – 6) = 102.4
120.4 – x2 – 3x = 102.4
x2 + 3x – 18 = 0
x = 3 and -6
Correct fuel charge = (2x + 0.4)
10) Answer: b)
Fuel charges = 160% of (30 * 0.6) = Rs.28.8
Rebate = 60% of Distance covered + 125% of fuel charges
= 60% of 30 + 125% of 28.8
= 18 + 36
= Rs.54
Total fare = 28.8 + 10 * 30 + 20 * 0.6 – 54
= 28.8 + 300 + 12 – 54
= Rs.286.8





