Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
[WpProQuiz 7302]
Data Interpretation
Directions (1 – 5): Read the following information carefully and answer the questions given below
The below graph shows number of days taken by the employees P, Q, R, S, T and U to complete the work independently.
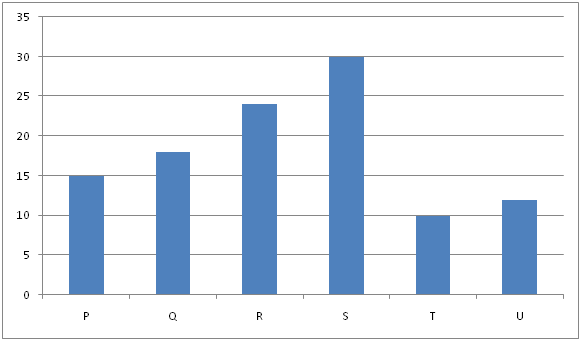
1) P worked for n days and then he left the organization. After that, Q and S works for the organization and finish the remaining work in (n + 2.5) days. The ratio of work done by P to Q and S together is 1: 2. Find how many days P worked.
a) 3 days
b) 4 days
c) 5 days
d) 6 days
e) 8 days
2) P and S starts working together, but P worked with 50% of his efficiency. R starts working with 66(2/3) % more of his efficiency on another work which is 62(1/2) % of the work which P and S were doing. Find the ratio of days taken by R to days taken by P and S together to complete the work?
a) 4: 5
b) 5: 6
c) 2: 5
d) 3: 5
e) 1: 3
3) S started the work and left the work after working for n days and then R joined the work and worked for m days. After R left, T completed the remaining work in 3 days. Find the number of days for which R and S worked individually, given that m is 200% of value of n?
a) 3 days and 7 days
b) 4 days and 5 days
c) 5 days and 11 days
d) 6 days and 12 days
e) 8 days and 16 days
4) Three persons R, S and T starts working on alternative day, starting from R then S and at last T. If R works with 66% more efficiently and S works with 75% of his efficiency and T works with half of his efficiency, then find in how many days total work completed?
a) 20 days
b) 21 days
c) 20 days
d) 22 days
e) 24 days
5) Three persons Q, S and U start working together. If Q works with 75% of his efficiency and S worked 25% more efficiently. All get 27180 Rupees as total wages. Find the individual wage of all the employees respectively.
a) 6795, 6795 and 13590
b) 13590, 6795 and 6795
c) 6795, 13590 and 6795
d) Cannot be determined
e) None of these
Caselet
Directions (6 – 10): Study the following information carefully and answer the given questions?
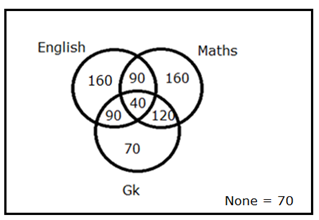
There are 800 students in a school. Out of the total number of students like one or more of three different subjects, viz English, Maths and GK while some people doesn’t like any of three subjects. Total number of students like all the three subjects is 5 % of total number of students in the school. Total number of students like Gk is 320. Total number of students doesn’t like those 3 subjects is equal to the total number of students like only GK. Total number of students like only English and GK is three-fourth of total number of students like only Maths and GK. Total number of students like only English is 70 more than the total number of students like only English and Maths. Total number of students like only GK is 30 more than the one-eighth of total number of students like GK. Total number of students like only Maths is 20 % of total number of students in the school.
6) How many students like at most two subjects in the school?
a) 760
b) 720
c) 680
d) 650
e) None of these
7) Total number of students like only English is what percentage more than the total number of students like all the 3 subjects?
a) 400 %
b) 320 %
c) 345 %
d) 300 %
e) None of these
8) Find the ratio between the total number of students like only one subject to that of total number of students like at least two subjects.
a) 43: 41
b) 39: 34
c) 45: 37
d) 54: 49
e) None of these
9) Find the total number of students like English and Maths but not GK.
a) 410
b) 390
c) 425
d) 440
e) None of these
10) If 35 % and 15 % of total number of students like only English and Maths respectively are changed their favourite subject to only GK, then find the total number of students like only GK.
a) 125
b) 140
c) 150
d) 160
e) None of these
Answers :
Direction (1-5) :
1) Answer: c)
LCM of 15, 18, 24, 30, 10 and 12 = 360
Hence P= 360/15 = 24, Q= 360/18= 20, S= 12,
Work done by P= 24n
Work done by Q and S in (n + 2.5) days = (Q + S) = 20 + 12 = 32
24n/(32 * (n + 2.5)) = 1/ 2
48n = 32n + 32 * 2.5
16n = 32 * 5/2
= > n = 5 days
2) Answer: d)
LCM of 15, 18, 24, 30, 10 and 12 = 360
Hence P= 360/15 = 24, R= 15, S= 12,
P worked with 50% of his efficiency = 12, S = 12
R starts working with 66(2/3) % more of his efficiency = > R = 25
62(1/2) % of the work = 62.5/100 = 5/8
R’s total work = 360 * 5/8 = 225
Hence, R/(P + S) = ( (225/25)/(360/(12 + 12))) = 9/15 = 3/5
3) Answer: d)
LCM of 15, 18, 24, 30, 10 and 12 = 360
Hence P= 360/15 = 24, Q= 360/18= 20, R= 15, S= 12, T= 36, U= 30
Work done by S= 12n, R=15m, T= 36*3= 108
12n+15m+108= 360
Since M=2n=> 12n+ 15*2n+ 108= 360
n= 6 days, m=12 days
4) Answer: c)
LCM of 15, 18, 24, 30, 10 and 12 = 360
Hence P= 360/15 = 24, Q= 360/18= 20, R= 15, S= 12, T= 36, U= 30
R works with 66% more efficiently =>25
S works with 75% of his efficiency=> 9
And T works with half of his efficiency=> 18
Work done by R and S and T for 3 days= 25+ 9+ 18= 52 => 3 days= 52
Multiply 6 both sides=> 52*6 = 3*6 => 312= 18 days
19th day R works, 20th day S works. Balance work 14. Hence 20 (14/18)
= > 20(7/9) days
5) Answer: a)
LCM of 15, 18, 24, 30, 10 and 12 = 360
Hence P= 360/15 = 24, Q= 360/18= 20, R= 15, S= 12, T= 36, U= 30
75% of Q’s efficiency= 15
S worked 25% more efficiently. Hence S= 15
U= 30
Q: S: U=15: 15: 30= 1: 1: 2
Total wage= 27180.
Hence Q’s share 6795, S’s share 6795 and U’s share 13590
Directions (6 – 10):
Total number of students doesn’t like those 3 subjects = Total number of students like only GK = G
A + B + C + D + E + F + G + G = 800 —> (1)
Total number of students likes all the three subjects (E)
= > 5 % of total number of students in the school
= > (5/100) * 800 = 40
Total number of students like Gk = 320
D + E + F + G = 320 —> (2)
Total number of students like only English and GK (D)
= > (3/4) * Total number of students like only Maths and GK (F)
D: F = 3 : 4 (3x, 4x)
Total number of students like only English is 70 more than the total number of students like only English and Maths
A – B = 70 –> (3)
Total number of students like only GK (G)
= > (1/8) * total number of students like GK + 30
= > (1/8) * 320 + 30 = 70
By solving the equation (2), we get,
3x + 40 + 4x + 70 = 320
= > 7x = 210
= > x = 30
Total number of students like only English and GK (D) = 90
Total number of students like only Maths and GK (F) = 120
Total number of students like only Maths (C) = (20/100) * 800 = 160
By solving the equation (1), we get,
A + B + C + D + E + F + G + G = 800 —> (1)
A + B + 160 + 90 + 40 + 120 + 70 + 70 = 800
A + B = 250 —> (4)
By solving the equation (3) and (4), we get,
A = 160, B = 90
Total number of students like only English (A) = 160
Total number of students like only English and Maths (B) = 90
6) Answer: a)
Total number of students likes at most two subjects
= > Total students in the school – total students like all the 3 subjects
= > 800 – 40 = 760
7) Answer: d)
Total number of students like only English = 160
Total number of students like all the 3 subjects = 40
Required % = [(160 – 40)/40] * 100 = 300 %
8) Answer: b)
The total number of students likes only one subject
= >160 + 160 + 70 = 390
The total number of students likes at least two subjects
= >90 + 40 + 90 + 120 = 340
Required ratio = 390: 340 = 39: 34
9) Answer: a)
The total number of students likes English and Maths but not GK
= > 160 + 90 + 160 = 410
10) Answer: c)
The total number of students likes only GK
= > 70 + 160 * (35/100) + 160 * (15/100)
= > 70 + 56 + 24 = 150





