Dear Aspirants, Our IBPS Guide team is providing new pattern Quantitative Aptitude Questions for IBPS PO Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS PO Mains Mock Test 2019
Data interpretation
Direction (1 – 5): Study the following data carefully and answer the questions:
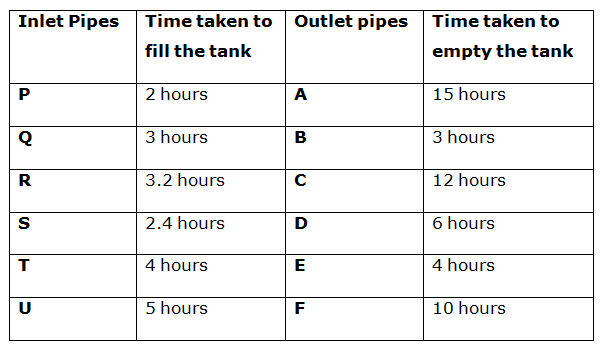
There are 6 inlet pipes P, Q, R, S, T and U and 6 outlet pipes A, B, C, D, E and F. Bar graph given below shows the time taken (hours) by 6 inlet pipes to fill a tank while the pie chart shows the per cent distribution of time taken (hours) by 6 outlet pipes to empty that tank.
Sum of the pie chart is 50 hours.
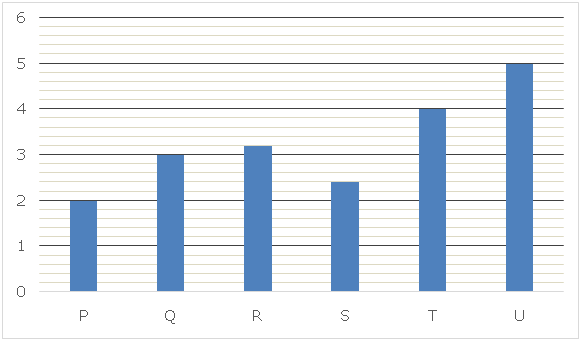
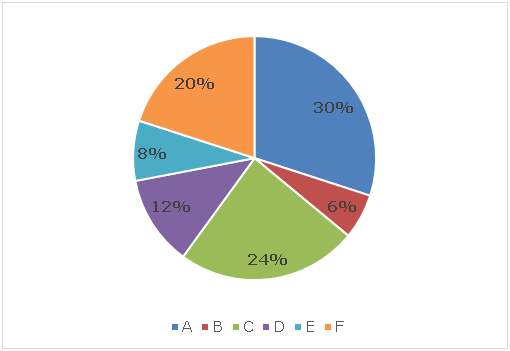
1) Time taken by pipes P and Q together to fill the tank when P is working with 80% of its original efficiency and pipe Q is working with 30% of its original efficiency is ‘T1’ and time taken by pipes P, Q and D together to fill that tank when all the pipes are working with its original efficiency is ‘T2’, then what is the difference between ‘T1’ and ‘T2’?
a) 45 minutes
b) 30 minutes
c) 50 minutes
d) 60 minutes
e) None of these
2) What is the total time taken by pipes U, A and F to fill the tank if all the three pipes are working alternatively for 1 hour each starting with pipe U followed by A and then by F? Assume pipe U is working with its efficiency 33(1/3)% more than its original efficiency, pipe F is working with half of its original efficiency and pipe A is working with its original efficiency?
a) 30 hours
b) 15 hours
c) 20 hours
d) 10 hours
e) None of these
3) Pipe T and C together start on the tank and after working for ‘N’ hours pipe T is replaced with pipe S and after working for 1 more hour pipe C is replaced with pipe D. Now, after working for 1 more hour pipe D stopped working and it takes 12 more minutes to fill the tank, then what is the value of ‘N’?
a) 2
b) 1.5
c) 3
d) 2.5
e) None of these
4) Two pipes R and E together can fill the tank in ‘N’ hours. If three pipes U, A and F together start filling that tank, then after how much time the pipe A should stop working so that total time taken to fill the tank in this arrangement is ‘N’ hours?
a) 6 hours
b) 7 hours
c) 8 hours
d) 9 hours
e) None of these
5) Three pipes R, S and D together start filling the tank and after working for 40 minutes pipe S is replaced by pipe C, then what is the total time taken by pipes R, C and D together to fill the remaining part of the tank?
a) 6 hours
b) 8 hours
c) 10 hours
d) 12 hours
e) None of these
Data Interpretation
Direction (6 – 10): Study the following data carefully and answer the questions:
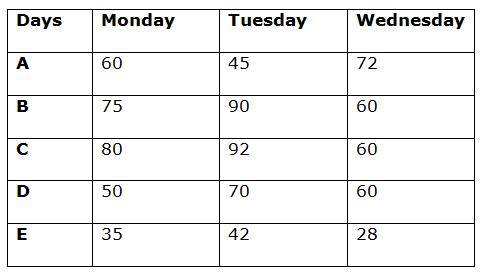
Pie chart given below shows the distribution (in degree) of speed (km/h) of five different persons A, B, C, D and E respectively on Monday and Total sum of pie chart is 300 km/h.
Line graph given below shows the per cent change in speed (km/h) of those five persons on Tuesday and Wednesday respectively with respect to Monday.
Note: Values in the line chart below 0% show the per cent decrease in the speed and values above 0% shows the per cent increment and all the per cent values are multiple of 5.
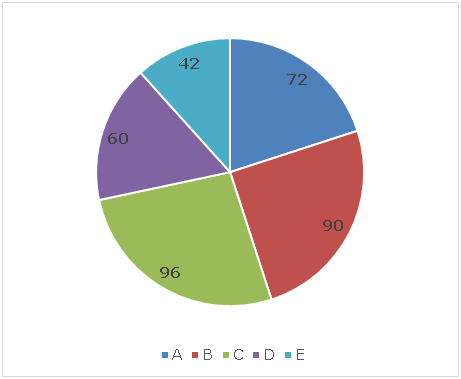
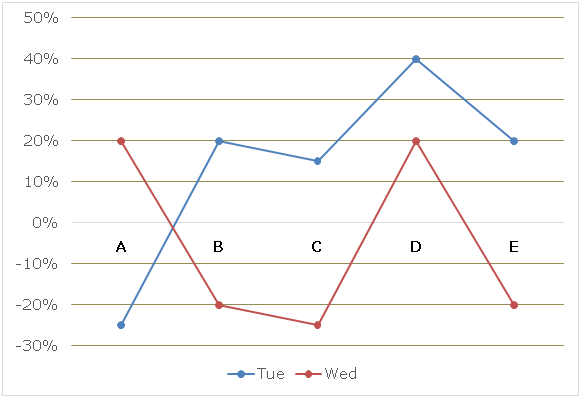
6) On Monday, persons A and D are initially ‘D’ km apart and they started travelling towards each other at the same time and meet after travelling for 45 minutes. What is the difference between the time taken by persons B and C to cover ‘D’ km on that day if person C is travelling with 25% less than his original speed?
a) 18.5 minutes
b) 16.5 minutes
c) 22.5 minutes
d) 10.5 minutes
e) None of these
7) If on Tuesday, persons A and E took part in a race in which A beats E by 2.4 km, then in the same race person B beats person D by ‘x’ km and person D beats person E by ‘y’ km, then what is the ratio of value of ‘x’ to that of ‘y’?
a) 7: 8
b) 4: 5
c) 5: 6
d) 5: 9
e) None of these
8) If person E goes from city P to city Q on Monday with speed ‘x’% less than his original speed and comes back from city Q to city P on Tuesday with speed ‘x + 5’% more than his original speed on that day and total time taken to cover his complete journey is 9 minutes more than time taken to complete journey with his original speed on both the days, then what is the total distance travelled by him on Wednesday in ‘x + 10’ minutes if distance between cities P and Q is 63 km?
a) 21 km
b) 14 km
c) 15 km
d) 12 km
e) None of these
9) On Wednesday, in total journey of ‘D’ km when A completed this journey, E was 154 km behind him. In the same distance when another person F completes this journey, person B was 84 km behind him, then what is the total time taken by persons E and F to meet with each other when they are initially88.5 km apart and travel towards each other?
a) 30 minutes
b) 36 minutes
c) 42 minutes
d) 45 minutes
e) None of these
10) Initially person A and D are ‘X’ km apart on Tuesday and they started travelling towards each other and they meet after travelling for 5.28 hours, then what is the ratio of time taken by person B and E together to meet with each other when travelling in same direction to that of in opposite direction and both B and E are initially ‘x’ km apart on Tuesday?
a) 13: 6
b) 7: 2
c) 11: 4
d) 19: 11
e) None of these
Answers :
Directions (1 – 5):
Time taken by pipe A to empty the tank = 30% of 50 = 15 hours
Time taken by pipe B to empty the tank = 6% of 50 = 3 hours
Time taken by pipe C to empty the tank = 24% of 50 = 12 hours
Time taken by pipe D to empty the tank = 12% of 50 = 6 hours
Time taken by pipe E to empty the tank =8% of 50 = 4 hours
Time taken by pipe F to empty the tank = 20% of 50 = 10 hours
1) Answer: b)
Time taken by pipe P alone when working with 80% of its original efficiency
= 2 * (100/80) = 2.5 hours
Time taken by pipe Q alone when working with 30% of its original efficiency
= 3 * (100/30) = 10 hours
T1 = 1/[(1/2.5) + (1/10)]
T1 = 2 hours
Time taken by pipes P, Q and D together to fill that tank when all the pipes are working with its original efficiency = T2 = 1/[(1/2) + (1/3) – (1/6)]
T2 = 1.5 hours
Required difference = 2 – 1.5 = 0.5 hours = 30 minutes
2) Answer: c)
Time taken by pipe U alone to fill the tank when working with 33(1/3)% more than its original efficiency = 5 * (3/4) = 3.75 hours
Time taken by pipe F alone to empty the tank when working with 50% of its original efficiency = 10 * 2 = 20 hours.
Since, all the pipes are opened for 1 hour each, then part of tank filled in first 3 hours = (1/3.75) – (1/20) – (1/15) = (16 – 3 – 4)/60 = 9/60 = 3/20
Time taken to fill whole tank = (20/3) * 3 = 20 hours
3) Answer: a)
Time taken by pipes S and T alone to fill the tank is 2.4 hours and 4 hours respectively and time taken by pipes C and D alone to empty the tank is 12 hours and 6 hours respectively.
Let total capacity of the tank = 24 (LCM of 2.4, 4, 12 and 6)
Part of tank filled by pipes S and T in one hour is 10 and 6 respectively.
Part of tank emptied by pipes C and D in one hour is 2 and 4 respectively.
Part of tank filled in first N hours = N * (6 – 2) = 4N
Part of tank filled in next 2 hours 12 minutes
= (10 – 2) + (10 – 4) + 10 * (12/60)
= 8 + 6 + 2 = 16
According to the question:
4N + 16 = 24
4N = 8
N = 2
4) Answer: d)
Time taken by pipes R and E together to fill the tank = N = 1/[(1/3.2) – (1/4)]
N = 16 hours
Let time after which pipe A should stop working = ‘T’ hours
According to the question:
T * [(1/5) – (1/15) – (1/10)] + (16 – T) * [(1/5) – (1/10)] = 1
(T/30) + 3(16 – T)/30 = 1
T + 48 – 3T = 30
2T = 48 – 30
T = 9 hours
5) Answer: c)
Part of tank fill by pipes R, S and D together is 40 minutes
= (40/60) * [(1/3.2) + (1/2.4) – (1/6)] = 3/8
Remaining part of the tank = 1 – (3/8) = 5/8
Part of tank filled by pipes R, C and D together in 1 hour
= (1/3.2) – (1/12) – (1/6) = 1/16
Required time taken to fill the remaining part of the tank = (5/8) ÷ (1/16)
= 10 hours
Directions (6 – 10):
Speed of person A on Monday = 300 * (72/360) = 60 km/h
Speed of person B on Monday = 300 * (90/360) = 75 km/h
Speed of person C on Monday = 300 * (96/360) = 80 km/h
Speed of person D on Monday = 300 * (60/360) = 50 km/h
Speed of person E on Monday = 300 * (42/360) = 35 km/h
Speed of person A on Tuesday = 75% of 60 = 45 km/h
Speed of person B on Tuesday = 120% of 75 = 90 km/h
Speed of person C on Tuesday = 115% of 80 = 92 km/h
Speed of person D on Tuesday = 140% of 50 = 70 km/h
Speed of person E on Tuesday = 120% of 35 = 42 km/h
Speed of person A on Wednesday = 120% of 60 = 72 km/h
Speed of person B on Wednesday = 80% of 75 = 60 km/h
Speed of person C on Wednesday = 75% of 80 = 60 km/h
Speed of person D on Wednesday = 120% of 50 = 60 km/h
Speed of person E on Wednesday = 80% of 35 = 28 km/h
6) Answer: b)
Effective speed of persons A and D together on Monday = 60 + 50 = 110 km
According to the question:
D = 110 * (45/60)
D = 110 * (3/4)
D = 330/4
D = 82.5 km
Time taken by person B to cover ‘D’ km on Monday = 82.5/75 = 1.1 hour
Time taken by person C to cover ‘D’ km on Monday = 82.5/ (75% of 80) = 1.375 hours
Required difference = 1.375 – 1.1 = 0.275 hours = 16.5 minutes
7) Answer: d)
Let time taken by A to finish the race =‘t’ hours
According to the question:
45t – 42t = 2.4
3t = 2.4
t = 0.8 hours
Length of the race = 45t = 45 * 0.8 = 36 km
Time taken by B to finish that race = 36/90 = 0.4 hours
In ‘0.4’ hours, distance travelled by D = 70 * 0.4 = 28 km
x = 36 – 28 = 8 km
Time taken by D to finish that race = 36/70 hours
In ‘36/70’ hours, distance travelled by E = 42 * (36/70) = 21.6 km
y = 36 – 21.6 = 14.4 km
Required ratio = x: y = 8: 14.4 = 5: 9
8) Answer: b)
Time taken to complete journey when travelling with original speed = (63/35) + (63/42) = 3.3 hours
Time taken for complete journey when travelling with changes speed = 3.3 + (9/60) = 3.45 hours
Changed speed of E on Monday = (100 – x)% of 35 = (35 – 0.35x)
Changed speed on E on Tuesday = (100 + x + 5)% of 42 = (44.1+ 0.42x)
According to the question:
[63/(35 – 0.35x)] + [63/(44.1 + 0.42x)] = 3.45 [9/(5 – 0.05x)] + [9/(6.3 + 0.06x)] = 3.45(6.3 + 0.06x)/ 5 – 0.05x)+ (5 – 0.05x) / (6.3 + 0.06x) = 3.45/9 = 23/60
60(11.3 + 0.01x) = 23(31.5 – 0.015x – 0.003x2)
678 + 0.6x = 724.5 – 0.345x – 0.069x2
0.069x2 + 0.945x – 46.5 = 0
x = 20
Distance covered by E on Wednesday in ‘x + 10’ minutes = 28 * (30/60) = 14 km
9) Answer: d)
Let total distance = ‘D’ km and person A completes this journey in ‘t’ hours.
According to the question:
72t – 28t = 154
44t = 154
t = 3.5
D = 72t = 252 km
Let the speed of person F = ‘F’ km/h and he completes this 252 km in ‘x’ hours.
Fx = 252 …….. (1)
Fx – 60x = 84
252 – 84 = 60x
x = 2.8
From equation (1):
F * 2.8 = 252
F = 90 km/h
Effective speeds of E and F when they are travelling towards each other = 90 + 28 = 118 km/h
Time after which persons E and F meet = 88.5/118 = 0.75 hours = 45 minutes
10) Answer: c)
Effective speed of person A and D on Tuesday when travelling towards each other = 45 + 70 = 115 km/h
According to the question:
x/115 = 5.28
x = 607.2 km
Effective speed of persons B and E when travelling in same direction = 90 – 42 = 48 km/h
Effective speed of persons B and E when travelling in opposite direction = 90 + 42 = 132 km/h
Time taken by persons B and E to meet with each other when travelling in same direction = 607.2/48 = 12.65 hours
Time taken by persons B and E to meet with each other when travelling in opposite direction = 607.2/132 = 4.6 hours
Required ratio = 12.65: 4.6 = 11: 4





