Dear Readers, Bank Exam Race for the Year 2019 is already started, To enrich your preparation here we have providing new series of Practice Questions on Quantitative Aptitude – Section. Candidates those who are preparing for NIACL AO Mains 2019 Exams can practice these questions daily and make your preparation effective.
[WpProQuiz 5213]
Click here to take NIACL AO Mock Test
Directions (Q. 1 – 5): In the following questions, two equations I and II are given. You have to solve both the equations and give answer as,
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or the relation cannot be established
1)
I) x2 + 19x – 92 = 0
II) 2y2 – 15y – 38 = 0
2)
I) 3x2 + 23x + 44 = 0
II) 4y2 – 6y – 28 = 0
3)
I) 6x – 7y + 2 = 3x – 2y
II) 2x – 3y = 0
4)
I) x = ∛19683 + 52 ÷ 4
II) y = √2401 – 32
5)
I) 2x2 – 25x + 77 = 0
II) 3y2 – 23y + 42 = 0
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following table represents number of different coloured balls contained by eight bags
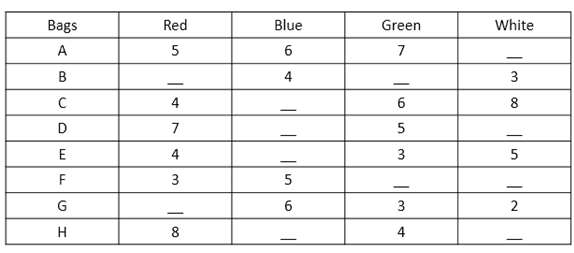
6) Probability of drawing one blue ball from bag A is 3/10. Probability of drawing one green ball from bag B is 1/3 and probability of drawing one blue ball from bag B is 2/9. Find the product of the probability of drawing 2 green balls from bag A and probability of drawing 2 red balls from bag B.
a) 4/855
b) 7/969
c) 5/876
d) 6/931
e) None of these
7) Probability of drawing one blue ball from bag B is 1/7. Probability of drawing one blue ball from bag D 1/9 and probability of drawing one green ball from bag D is 5/18. Find the ratio of the probability of drawing 2 green balls from bag C and probability of drawing 2 white balls from bag D.
a) 53:49
b) 48:25
c) 51:28
d) 37:21
e) None of these
8) Probability of drawing one white ball from bag E is 1/3. Probability drawing one green ball from bag F is 2/9 and probability of drawing one red ball from bag F is 1/6. Probability of drawing one green ball from bag E is what percent of probability of drawing one blue ball from bag F?
a) 72%
b) 68%
c) 64%
d) 56%
e) None of these
9) Probability of drawing one red ball from bag H is 2/5 and probability of drawing one green ball from bag H is 1/5. Find the probability of drawing four balls of different colour from bag H.
a) 5/696
b) 3/712
c) 4/969
d) Cannot be determined
e) None of these
10) Probability of drawing one green ball from bag G is 1/5. Probability of drawing one white ball from bag H is ¼ and probability of drawing one green ball from bag H is 1/5.Find the sum of the probability of drawing two blue balls from bag G and probability of drawing 2 green balls from bag H.
a) 109/515
b) 113/525
c) 111/413
d) 116/665
e) None of these
Answers :
Direction (1-5) :
1) Answer: e)
I) x2 + 19x – 92 = 0
(x + 23) (x – 4) = 0
X = -23, 4
II) 2y2 – 15y – 38 = 0
2y2 + 4y – 19y – 38 = 0
2y (y + 2) -19 (y + 2) = 0
(2y – 19) (y + 2) = 0
Y = 19/2, -2 = 9.5, -2
Can’t be determined
2) Answer: c)
I) 3x2 + 23x + 44 = 0
3x2 + 12x + 11x + 44 = 0
3x (x + 4) + 11 (x + 4) = 0
(3x + 11) (x + 4) = 0
X = -11/3, -4 = -3.66, -4
II) 4y2 – 6y – 28 = 0
4y2 + 8y – 14y – 28 = 0
4y (y + 2) -14 (y + 2) = 0
(4y – 14) (y + 2) = 0
Y = 14/4, -2 = 3.5, -2
X < y
3) Answer: a)
I) 6x – 7y + 2 = 3x – 2y
3x – 5y = -2 –> (1)
II) 2x – 3y = 0 —> (2)
By solving the equation (1) and (2), we get,
X = 6, y = 4
X > y
4) Answer: e)
I) x = ∛19683 + 52 ÷ 4
X = 27 + (52/4)
X = 27 + 13 = 40
II) y = √2401 – 32
Y = 49 – 9 = 40
X = y
5) Answer: a)
I) 2x2 – 25x + 77 = 0
2x2 – 11x – 14x + 77 = 0
X (2x – 11) – 7 (2x – 11) = 0
(x – 7) (2x – 11) = 0
X = 7, 11/2 = 7, 5.5
II) 3y2 – 23y + 42 = 0
3y2 – 9y – 14y + 42 = 0
3y (y – 3) -14(y – 3) = 0
(3y – 14) (y – 3) = 0
Y = 14/3, 3 = 4.66, 3
X > y
Direction (6-10) :
6) Answer: b)
Let, the number of white balls in bag A = n
Total number of balls in bag A = 5 + 6 + 7 + n = 18 + n
6/(18 + n) = 3/10
=> 60 = 54 + 3n
=> 3n = 60 – 54
=> 3n = 6
=> n = 2
Total number of balls in bag A = 18 + 2 = 20
Probability of drawing 2 green balls from bag A = 7c2/20c2
= (7 x 6)/(20 x 19)
= 21/190
Let, the number of red balls in bag B = x
And number of green balls in bag B = y
Total number of balls in bag B = 4 + 3 + x + y = (7 + x + y)
y/(7 + x + y) = 1/3
=> 3y = 7 + x + y
=>x – 2y = -7 —— (i)
4/(7 + x + y) = 2/9
=> 36 = 14 + 2x + 2y
=> 2x + 2y = 22
=> x + y = 11 —— (ii)
Equation (ii) – equation (i)
x + y – x + 2y = 11 + 7
=> 3y = 18
=> y = 6
Putting the value of y in equation (ii)
x + 6 = 11
=> x = 11 – 6
=> x = 5
Total number of balls in bag B = 7 + 5 + 6 = 18
Probability of drawing 2 red balls from bag B = 5c2/18c2
= (5 x 4)/(18 x 17)
= 10/153
Required product = 21/190 x 10/153 = 7/969
7) Answer: c)
Let the number of blue balls in bag C = n
Total number of balls in bag C = (4 + 6 + 8 + n) = 18 + n
n/(18 + n) = 1/7
=> 7n = n + 18
=> 7n – n = 18
=> 6n = 18
=> n = 3
Total number of balls in bag C = 18 + 3 = 21
Probability of drawing 2 green balls from bag C = 6c2/21c2
= (6 x 5)/(21 x 20)
= 1/14
Let, the number of blue balls in bag D = x
And number of white balls in bag D = y
Total number of balls in bag D = 7 + 5 + x + y = 12 + x + y
x/(12 + x + y) = 1/9
=> 9x = 12 + x + y
=> 8x – y = 12 —— (i)
5/(12 + x + y) = 5/18
=> 90 = 60 + 5x + 5y
=> 5x + 5y = 30
=> x + y = 6 —– (ii)
Adding equations (i) and (ii)
8x – y + x + y = 12 + 6
=> 9x = 18
=> x = 2
Putting the value of x in equation (ii)
2 + y = 6
=> y = 6 – 2
=> y = 4
Total number of balls in bag D = 12 + 2 + 4 = 18
Probability of drawing 2 white balls from bag D = 4c2/18c2
= (4 x 3)/(18 x 17)
= 2/51
Required ratio = 1/14: 2/51 = 51:28
8) Answer: a)
Let the number of blue balls in bag E = n
Total number of balls in bag E = 4 + 3 + 5 + n = 12 + n
5/(12 + n) = 1/3
=> 15 = 12 + n
=> n = 3
Total number of balls in bag E = 12 + 3 = 15
Probability of drawing one green ball from bag E = 3/15 = 1/5
Let the number of green balls in bag F = x
And number of white balls in bag F = y
Total number of balls in bag F = 3 + 5 + x + y = 8 + x + y
x/(8 + x + y) = 2/9
=> 9x = 16 + 2x + 2y
=> 7x – 2y = 16 —– (i)
3/(8 + x + y) = 1/6
=> 18 = 8 + x + y
=> x + y = 10 —— (ii)
Equation (i) – 7 x equation (ii)
7x – 2y – 7x – 7y = 16 – 70
=> -9y = -54
=> y = 6
Putting the value of y in equation (ii)
x + 6 = 10
=> x = 4
Total number of balls in bag F = 8 + 4 + 6 = 18
Probability of drawing one blue ball from bag F = 5/18
Required percentage = (1/5)/(5/18) x 100
= 1/5 x 18/5 x 100
= 18/25 x 100
= 72%
9) Answer: d)
Let, the number of blue balls in bag H = x
And number of white balls in bag H = y
Total number of balls in bag H = 8 + 4 + x + y = 12 + x + y
8/(12 + x + y) = 2/5
=> 40 = 24 + 2x + 2y
=> 2x + 2y = 40 – 24
=> 2x + 2y = 16
=> x + y = 8
4/(12 + x + y) = 1/5
=> 20 = 12 + x + y
=> x + y = 8
Hence, required value cannot be find out.
10) Answer: d)
Let, the number of red balls in bag G = n
Total number of balls in bag G = 6 + 3 + 2 + n = 11 + n
3/(11 + n) = 1/5
=> 15 = 11 + n
=> n = 4
Total number of balls in bag G = 11 + 4 = 15
Probability of drawing two blue balls from bag G = 6c2/15c2
= (6 x 5)/(15 x 14)
= 1/7
Let, the number of blue balls in bag H = x
And number of white balls in bag H = y
Total number of balls in bag H = 8 + 4 + x + y = 12 + x + y
y/(12 + x + y) = ¼
=> 4y = 12 + x + y
=>x – 3y = -12 —— (i)
4/(12 + x + y) = 1/5
=> 20 = 12 + x + y
=> x + y = 8 —– (ii)
Equation (i) – equation (ii)
x – 3y – x – y = – 12 – 8
=> -4y = – 20
=> y = 5
Putting the value of y in equation (i)
x – 15 = -12
=> x = 15 – 12
=> x = 3
Total number of balls in the bag = 12 + 3 + 5 = 20
Probability of drawing 2 green balls from bag H = 4c2/20c2
= (4 x 3)/(20 x 19)
= 3/95
Required sum = 1/7 + 3/95
= (95 + 21)/665
= 116/665





