Dear Readers, Exam Race for the Year 2019 has already started, To enrich your preparation here we are providing new series of Practice Questions on Quantitative Aptitude – Section for CWC/FCI Exam. Aspirants, practice these questions on a regular basis to improve your score in aptitude section. Start your effective preparation from the right beginning to get success in upcoming CWC/FCI Exam.
[WpProQuiz 5687]Click Here to Take FCI Prelims Mock Test
Click Here to Take CWC Prelims Mock Test
Directions (Q. 1 – 5): Each question contains a statement followed by Quantity I and II. Read the contents clearly and answer your questions accordingly and Give answer as,
a) Quantity I > Quantity II
b) Quantity I ≥ Quantity II
c) Quantity II > Quantity I
d) Quantity II ≥ Quantity I
e) Quantity I = Quantity II or Relation cannot be established
1) Quantity I: 5 years ago, the ratio of age of A and B is 2: 3. After 2 years, the sum of their ages is 44. Then find the present age of A
Quantity II: 5 years ago, the ratio of age of P and Q is 3: 4. P’s age after 6 years is equal to the present age of Q. Then find the present age of P
2) Quantity I: The difference between the simple interest and compound interest on a certain sum of money for 2 years at 12 % per annum is Rs. 432. Find the sum
Quantity II: A certain sum of money invested for a period of 4 years at 15 % per annum, simple interest earned is Rs. 15000. Find the principle
3) Quantity I: The shopkeeper sold an article at 25 % discount on marked price and he gains 10 %. If the marked price of the article is Rs. 660, then find the cost price?
Quantity II: The shopkeeper marks the book for Rs. 400 and his profit percentage is 20%. Find the cost price of the book, if he allows a discount 10 %?
4) Quantity I: The ratio of speed of two trains is 3: 5. If the faster train runs 350 km in 7 hours, then the speed of the slower train is?
Quantity II: 150 m long train crosses a telegram post in 12 sec. Find the speed of the train
5) Quantity I: If the length of a rectangle is increased by 15% while the breadth of the rectangle is decreased by 20% then find percentage change in area of the rectangle?
Quantity II: If the breadth of a triangle is increased by 20 % while the height of a triangle is decreased by 10 %, then find the percentage change in area of the triangle?
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions:
The following pie chart shows the total number of passengers in 5 different trains (A, B, C, D and E).
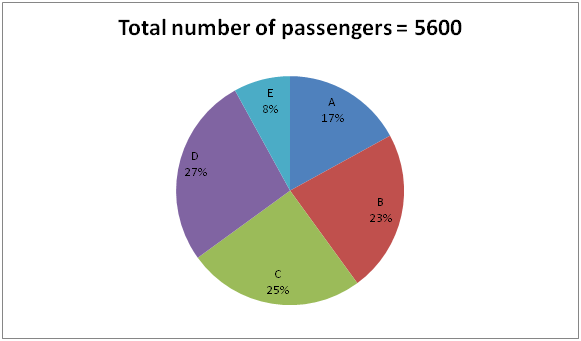
6) Find the difference between the total number of passengers in train A and C together to that of the train B and D together?
a) 372
b) 448
c) 512
d) 396
e) None of these
7) Find the average number of passengers in train C, D and E together?
a) 1120
b) 980
c) 756
d) 1042
e) None of these
8) Total number of passengers in train E is what percentage of the total number of passengers in train C?
a) 46 %
b) 54 %
c) 32 %
d) 28 %
e) None of these
9) If the cost of AC ticket in train E is Rs. 500 and the ratio of passengers in AC, Sleeper class and Unreserved category in train E is 3: 3 :2, then find the total cost paid by the AC class passengers in train E?
a) Rs. 91000
b) Rs. 80500
c) Rs. 75500
d) Rs. 84000
e) None of these
10) If the ratio of men, women and children in train C is 3: 2: 2, then find the total number of men in train C?
a) 450
b) 600
c) 520
d) 560
e) None of these
Answers :
Direction (1-5) :
1) Answer: c)
Quantity I:
5 years ago, the ratio of age of A and B = 2: 3 (2x, 3x)
According to the question,
2x + 3x + 14 = 44
5x = 30
= > x = 6
The present age of A = 2x + 5 = 17 years
Quantity II:
5 years ago, the ratio of age of P and Q = 3: 4 (3x, 4x)
According to the question,
3x + 5 + 6 = 4x + 5
= > x = 6
The present age of P = 3x + 5 = 18 + 5 = 23 years
Quantity I < Quantity II
2) Answer: a)
Quantity I:
The difference between the simple interest and compound interest for 2 years,
Diff = Sum*(r/100)2
432 = Sum*(12/100)2
(432*100*100)/144 = Sum
Sum = Rs. 30000
Quantity II:
- I = Pnr/100
15000 = (P*4*15)/100
(15000*100)/60 = P
Principle = Rs. 25000
Quantity I > Quantity II
3) Answer: a)
Quantity I:
660*(75/100) = CP*(110/100)
CP = 660*(75/100)*(100/110) = Rs. 450
Quantity II:
400*(90/100) = CP*(120/100)
CP = 400*(90/100)*(100/120) = Rs. 300
Quantity I > Quantity II
4) Answer: c)
Quantity I:
The ratio of speed of two trains = 3: 5 (3x, 5x)
The speed of faster train = 350/7 = 50 km/hr
5x = 50
= > x = 10
The speed of slower train = 3x = 30 km/hr
Quantity II:
The speed of the train = 150/12 = (150/12)*(18/5) = 45 km/hr
Quantity II > Quantity I
5) Answer: e)
Quantity I:
Let the length and breadth be 10 m and 10m respectively.
Normal Area = lb = 10*10 = 100 Sq m
New Area = (10*115/100)*(10*80/100) = 11.5*8 = 92 Sq m
Percentage change = [(100 – 92)/100]*100 = (8/100)*100 = 8 % decreased
Quantity II:
Let the breadth and height of a triangle be 10 m and 10 m respectively.
Normal area = (1/2)*b*h = (1/2)*10*10 = 50 Sq m
New area = (1/2)*(10*120/100)*(10*90/100) = (1/2)*12*9 = 54 Sq m
Percentage change = [(54 – 50)/50]*100 = 8 % increased
Quantity I = Quantity II
Direction (6-10) :
6) Answer: b)
Required difference = [5600*(23 + 27)/100] – [5600*(17 + 25)/100]
= > (5600/100)*[50 – 42] = 56*8
= > 448
7) Answer: a)
The average number of passengers in train C, D and E together
= > 5600*[(25 + 27 + 8)/300]
= > 1120
8) Answer: c)
Required % = (8/25)*100 = 32 %
9) Answer: d)
Total number of passengers in train E = 5600*(8/100) = 448
The ratio of passengers in AC, Sleeper class and Unreserved in train E
= > 3: 3: 2
8’s = 448
1’s = 56
The cost of AC ticket in train E = Rs. 500
The total cost paid by the AC class passengers in train E
= > (56*3)*500 = Rs. 84000
10) Answer: b)
Total number of passengers in train C
= > 5600*(25/100) = 1400
The ratio of men, women and children in train C = 3: 2: 2
7’s = 1400
1’s = 200
Total number of men in train C = 600





