Dear Readers, Exam Race for the Year 2019 has already started, To enrich your preparation here we are providing new series of Practice Questions on Quantitative Aptitude – Section for CWC/FCI Exam. Aspirants, practice these questions on a regular basis to improve your score in aptitude section. Start your effective preparation from the right beginning to get success in upcoming CWC/FCI Exam.
[WpProQuiz 5759]Click Here to Take FCI Prelims Mock Test
Click Here to Take CWC Prelims Mock Test
Directions (1 – 5): Read the following information carefully and answer the given questions.
In a class total 210 students (140 boys and 70 girls) like at least one of the three different subjects viz. History, Geography and Botany.
Boys: 30 boys like only History. The ratio of the boys like History and Geography but not Botany, Geography and Botany but not History and History and Botany but not Geography is 4: 1: 2. 65 boys like only one subject and 5 boys like all the three subjects.
Girls: 15 girls like only History. 30 girls like Botany and 5 girls like all the three subjects which is 1/4th of the girls like only Geography.
1) Find the number of boys like History and Botany but not Geography?
a) 10
b) 15
c) 20
d) 5
e) 25
2) If girls like History & Geography but not Botany, All the three subjects and History & Botany but not Geography is same and the girls like Geography & Botany but not History and only Botany is in the ratio 1: 1. Then find the number of girls like Geography?
a) 30
b) 25
c) 35
d) 40
e) 15
3) Number of boys like only History is what percent more than the number of girls like only History?
a) 150%
b) 100%
c) 200%
d) 50%
e) None of these
4) What is the ratio of the boys like Geography to that of the girls like Botany, if boys like only Geography is 5/28th of the total boys?
a) 8: 3
b) 4: 5
c) 2: 3
d) 6: 7
e) None of these
5) Find the girls like at least two subjects, if girls like only Botany is twice the girls like all the three subjects?
a) 20
b) 15
c) 10
d) 30
e) 25
Directions (6 – 10): The following questions are accompanied by two statements I and II. You have to determine which statement is/are sufficient to answer the questions.
6) Ragu goes to a certain point upstream and back to the starting point in the river. Speed of downstream is 10 km/hr. Find the average speed of the boat
Statement I: Ragu goes 60 km upstream in 12 hours.
Statement II: Speed of boat in still water is 8 km/hr.
a) Only I is sufficient to answer the question
b) Only II is sufficient to answer the question
c) Both I and II together is sufficient to answer the question
d) Both the statements are not sufficient to answer the question
e) Either I or II is sufficient to answer the question
7) If both the pipes A and B are opened, then find the time taken to fill the tank?
Statement I: Pipe A fills the tank alone in 6 hours.
Statement II: Pipe B alone empties the full tank in 15 hours.
a) Only I is sufficient to answer the question
b) Only II is sufficient to answer the question
c) Both I and II together is sufficient to answer the question
d) Both the statements are not sufficient to answer the question
e) Either I or II is sufficient to answer the question
8) Find the speed of train B in km/hr, if the length of train B is twice that of train A?
Statement I: Train A crosses a pole in 10 sec at the speed of 12 m/s.
Statement II: The length of platform is 250 m. Train B crosses the platform in 49 sec.
a) Only I is sufficient to answer the question
b) Only II is sufficient to answer the question
c) Both I and II together is sufficient to answer the question
d) Both the statements are not sufficient to answer the question
e) Either I or II is sufficient to answer the question
9) Find the ratio of boys to that of girls in the school?
Statement I: There are 750 students in the school.
Statement II: The number of boys in the school is 125 % that of girls.
a) Only I is sufficient to answer the question
b) Only II is sufficient to answer the question
c) Both I and II together is sufficient to answer the question
d) Both the statements are not sufficient to answer the question
e) Either I or II is sufficient to answer the question
10) Find the profit earned by the shopkeeper, if the marked price of the article is Rs. 500?
Statement I: The shopkeeper allowed a discount of 15 % and the cost price of the article is Rs. 340.
Statement II: The selling price of the article is Rs. 425.
a) Only I is sufficient to answer the question
b) Only II is sufficient to answer the question
c) Both I and II together is sufficient to answer the question
d) Both the statements are not sufficient to answer the question
e) Either I or II is sufficient to answer the question
Answers :
Directions (1 – 5):
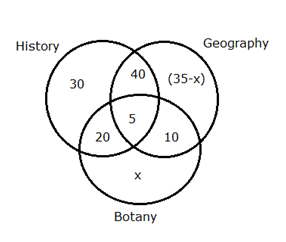
Boys:
Boys like only History = 30
Boys like all the three subjects = 5
Boys like only one subject = 65
Boys like only Two subject = Total – Only one subject – all the three subjects
= 140 – 65 – 5
= 70
The ratio of the boys like History and Geography but not Botany, Geography and Botany but not History and History and Botany but not Geography
= 4: 1: 2
Boys like History & Geography but not Botany = 70 * 4/7 = 40
Boys like Geography & Botany but not History = 70 * 1/7 = 10
Boys like History & Botany but not Geography = 70 * 2/7 = 20
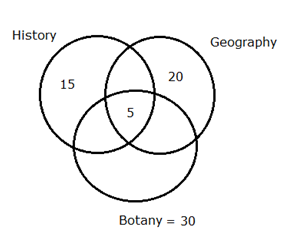
Girls:
15 girls like only History. 30 girls like Botany and 5 girls like all the three subjects which is 1/4th of the girls like only Geography.
Girls like only History = 15
Girls like all the three subjects = 5
Girls like only Geography = 4*5 = 20
Girls like Botany = 30
1) Answer: c)
Boys like History & Botany but not Geography = 20
2) Answer: d)
Girls like History & Geography but not Botany = All the three subjects = History & Botany but not Geography = 5
The girls like Geography & Botany but not History and only Botany
= 70 – (15+5+20+5+5)
= 70 – 50
= 20
Girls like Geography & Botany but not History = 20 *1/2 = 10
Girls like only Botany = 20 *1/2 = 10
Girls like Geography = 20 + 5 + 5 + 10 = 40
3) Answer: b)
Required percentage = [(30-15)/15]*100
= (15/15)*100 = 100%
4) Answer: a)
Boys like only Geography = 140 * 5/28
= 5*5 = 25
Boys like Geography = (25+5+40+10)
= 80
Girls like Botany = 30
Required ratio = 80: 30 = 8: 3
5) Answer: e)
Girls like only Botany = 5 * 2 = 10
Girls like at least two subjects = 70 – (15+10+20)
= 70 – 45
= 25
Direction (6-10) :
6) Answer: e)
Speed of downstream = 10 km/hr
From I,
Speed of upstream = D/T = 60/12 = 5 km/hr
Average speed of the boat = 2xy/(x + y) = (2*10*5)/15 = 20/3 km/hr
Statement I is sufficient to answer the question
From II,
Speed of boat in still water = 8 km/hr
= ½ *(Downstream speed + upstream speed)
16 = Downstream speed + upstream speed
16 = 10 + upstream speed
Upstream speed = 6 km/hr
Average speed of the boat = 2xy/(x + y) = (2*10*6)/16 = 7.5 km/hr
Statement II is sufficient to answer the question
Either I or II is sufficient to answer the question.
7) Answer: c)
From I and II,
The time taken to fill the tank
= > (1/6) – (1/15) = 1/10
10 hours taken to fill the tank.
So, both statement I and II are sufficient to answer the question.
8) Answer: c)
From I,
The speed of train A = 12*10 = 120 m
Length of train A = 120 m, Length of train B = 240
From II,
The length of platform = 250 m
From I and II,
Speed of train B = (240 + 250)/49
= 490/49 = 10 m/s
= 10*(5/18) = 25/9 km/hr
Both statements I and II are sufficient to answer the question.
9) Answer: b)
From I,
Total students in the school = 750
From II,
Boys = (125/100)*Girls
The ratio of boys to girls = 125: 100 = 5: 4
Statement II is sufficient to answer the question
10) Answer: a)
From I,
500*(85/100) = 340*[(100 + P %)/100]
425 = (34/10)*(100 + P %)
125 = 100 + P %
P % = 125 – 100 = 25 %
Statement I is sufficient to answer the question.
From II,
The selling price of the article = Rs. 425
From that, we can to find only discount %.
Statement II is not sufficient to answer the question.





