Dear Readers, Exam Race for the Year 2019 has already started, To enrich your preparation here we are providing new series of Practice Questions on Quantitative Aptitude – Section for CWC/FCI Exam. Aspirants, practice these questions on a regular basis to improve your score in aptitude section. Start your effective preparation from the right beginning to get success in upcoming CWC/FCI Exam.
[WpProQuiz 5867]Click Here to Take FCI Prelims Mock Test
Click Here to Take CWC Prelims Mock Test
Directions (1 – 5): Study the following information carefully and answer the questions given below:
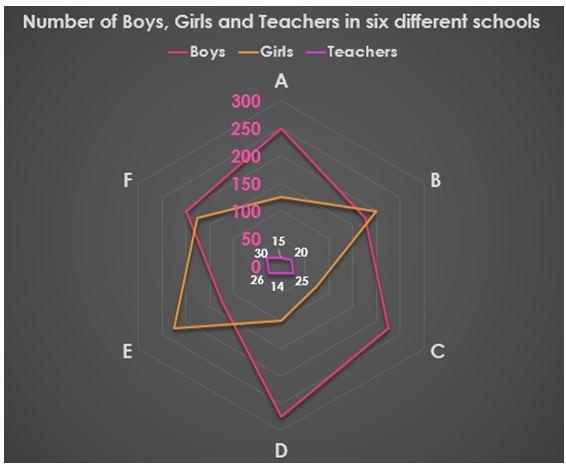
1) Sum of total number of boys, girls and teachers in school A is what percent of the sum of total number of boys, girls and teachers in school D?
a) 101.23%
b) 100.25%
c) 102.32%
d) 103.15%
e) None of these
2) Find the respective ratio between total number of boys, girls and teachers in school B and that in school C.
a) 67:81
b) 81:67
c) 65:79
d) 79:65
e) None of these
3) Find the difference between total number of boys and total number of girls from all the schools together.
a) 300
b) 350
c) 450
d) 500
e) None of these
4) Total number of boys, girls and teachers of school E is what percent more/less than the total number of boys, girls and teachers of school F?
a) 7.1% less
b) 8.2% more
c) 7.1% more
d) 8.2% less
e) None of these
5) Find the sum of total number of teachers from all the schools together and total number of students of schools A and C.
a) 850
b) 660
c) 665
d) 805
e) None of these
Directions (6 – 10): In each of these questions two equations (I) and (II) are given. You have to solve both the equations and give answer
a) If x > y
b) If x ≥ y
c) If x < y
d) If x ≤ y
e) If x = y or no relation can be established between x and y
6)
I. 6x2 – 19x + 15 =0
II. 10y2 – 29y – 21 =0
7)
I. 5x2 -16x +11 =0
II. 5y2 -3y =2
8)
I. x2 + 18x+72 =0
II. Y2 + 6y +8 =0
9)
I. 8x2 -22x +15 =0
II. 3y2-13y +14 =0
10)
I. 9x2 -26x +16 =0
II. 3y2 -16y+ 20 =0
Answers:
Directions (1-5):
1) Answer: b)
Sum of total number of boys, girls and teachers in school A = 250 + 125 + 15
= 390
Sum of total number of boys, girls and teachers in school D = 275 + 100 + 14
= 389
Required percentage = 390/389 x 100 = 100.25%
2) Answer: d)
Total number of boys, girls and teachers in school B = 175 + 200 + 20 = 395
Total number of boys, girls and teachers in school C = 225 + 75 + 25 = 325
Required ratio = 395:325 = 79:65
3) Answer: b)
Total number of boys from all the schools together = 250 + 175 + 225 + 275 + 125 + 200 = 1250
Total number of girls from all the schools together = 125 + 200 + 75 + 100 + 225 + 175 = 900
Required difference = 1250 – 900 = 350
4) Answer: a)
Total number of boys, girls and teachers of school E = 125 + 225 + 26 = 376
Total number of boys, girls and teachers of school F = 200 + 175 + 30 = 405
Required percentage = (405 – 376)/405 x 100 = 7.1% less
5) Answer: d)
Total number of teachers from all the schools together
= 15 + 20 + 25 + 14 + 26 + 30 = 130
Total number of students of school A = 250 + 125 = 375
Total number of students of school C = 225 + 75 = 300
Required sum = 130 + 375 + 300 = 805
Directions (6-10):
6) Answer: e)
I. 6x2 – 19x + 15 =0
6x2 – 9x-10x + 15 =0
3x(2x-3) -5(2x-3) =0
(3x-5) (2x-3) =0
x= 5/3, 3/2
II. 10y2 – 29y – 21 =0
10y2 – 35y +6y -21 =0
5y (2y-7)+3 (2y-7) =0
(5y+3) (2y-7) =0
y= -3/5, 7/2
Can’t be determined
7) Answer: b)
I. 5x2 -16x +11 =0
5x2 -11x-5x +11 =0
x(5x-11)-1(5x-11)=0
(x-1) (5x-11)=0
x=1, 11/5
II. 5y2 – 3y – 2 =0
5y2 – 5y+2y – 2 =0
5y(y-1)+2(y-1)=0
(5y+2)(y-1) =0
y = -2/5, 1
Hence, x ≥ y
8) Answer: c)
I. x2 + 18x+72 =0
x2 + 12x +6x +72 =0
x(x+12)+6 (x+12) =0
(x+6) (x+12) =0
x=-6, -12
II. Y2 + 6y +8 =0
Y2 + 4y+2y +8 =0
Y(y+4)+2 (y+4) =0
(y+2) (y+4) =0
Y =-2, -4
Hence, x<y
9) Answer: c)
I. 8x2 -22x +15 =0
8x2 -12x-10x +15 =0
4x (2x-3)-5(2x-3) =0
(4x-5) (2x-3) =0
x= 5/4, 3/2
II. 3y2-13y +14 =0
3y2-6y -7y +14 =0
3y(y-2)-7(y-2) =0
(3y-7)(y-2)=0
y=7/3, 2
Hence, x<y
10) Answer: d)
I. 9x2 -26x +16 =0
9x2 -18x -8x +16 =0
9x(x-2)-8 (x-2) =0
(9x-8) (x-2) =0
x=8/9, 2
II. 3y2 -16y+ 20 =0
3y2 -10y-6y + 20 =0
y (3y-10)-2(3y-10) =0
(y-2) (3y-10) =0
y =2, 10/3
Hence, x ≤ y





