Dear Aspirants, Our IBPS Guide team is providing a new series of Quantitative Aptitude Questions for SBI Clerk Mains 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.
Check here for IBPS RRB Clerk Prelims Mock Test 2019
Check here for SBI Clerk Mains Mock Test 2019
Click Here to Subscribe Crack High Level Puzzles & Seating Arrangement Questions PDF 2019 Plan
[WpProQuiz 6803]
Directions (1 – 5): Study the following information carefully and answer the questions given below:
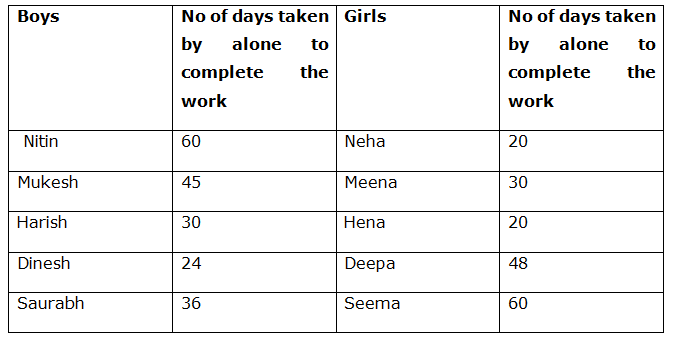
The following bar graph represents time taken by five pairs of a boy and a girl together to complete a piece of work.
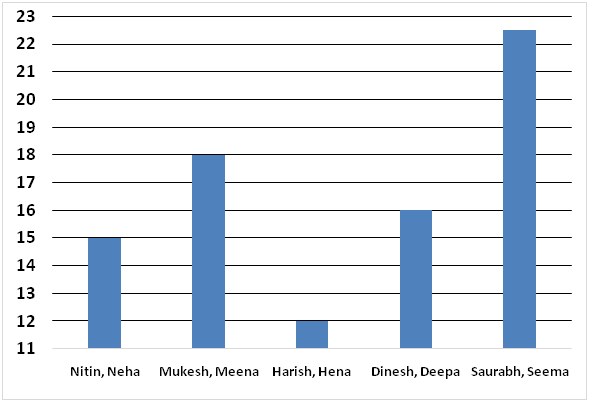
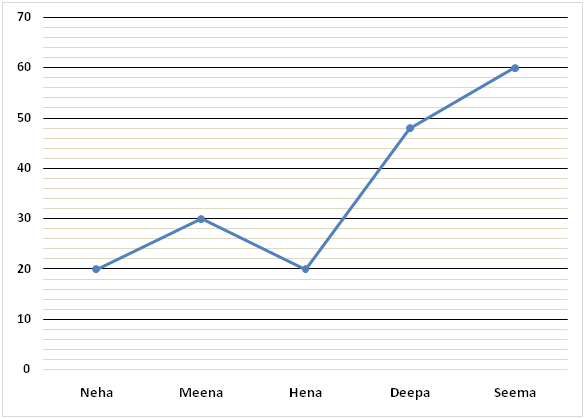
The following line graph represents time taken by five girls to complete the work alone.
1) Find the respective ratio of the sum of the efficiencies of Meena and Harish and sum of the efficiencies of Seema and Dinesh.
a) 10: 9
b) 8: 7
c) 7: 6
d) 5: 4
e) None of these
2) Nitin started the work and left after 12 days. Find the time taken by Deepa and Saurabh to complete the remaining part of the work together.
a) 913/33 days
b) 452/23 days
c) 683/27 days
d) 576/35 days
e) None of these
3) Time taken by Neha and Harish to complete the work together is approximately what percent of the time taken by Hena and Mukesh to complete the work together?
a) 47%
b) 53%
c) 79%
d) 93%
e) 87%
4) Find the time taken by Nitin, Harish, Hena and Meena to complete the work together.
a) 9 days
b) 15/2 days
c) 8 days
d) 17/2 days
e) None of these
5) Saurabh and Dinesh started the work. Seema joined them on thirteenth day. All three continued till the work completed. Find the number of days for which Seema worked.
a) 30/11 days
b) 40/21 days
c) 50/23 days
d) 60/31 days
e) None of these
6) 5 years ago, the age of a man was 7 year more than 4 times the age of his son. After 3 years, the age of the man will be 2 years less than thrice the age of his son. After how many years will the sum of their ages be 90 years?
a) 19 years
b) 10 years
c) 36 years
d) 23 years
e) None of these
7) A, B and C started a business by investing in the ratio of 4: 5: 8. After 4 months, A invested 50 % more than the initial investment and after another 2 months, B withdraws two-fifth of the initial investment. Find the share of C, if the total profit at the end of the year is Rs. 98800?
a) Rs. 45600
b) Rs. 42400
c) Rs. 48200
d) Rs. 50800
e) None of these
8) A sum was put at certain rate of simple interest for 5 years. If the interest would have been 4 % higher than the previous rate then Rs. 6000 would have been earned more. Find the sum?
a) Rs. 32000
b) Rs. 28000
c) Rs. 30000
d) Rs. 36000
e) None of these
9) Pipe P and Q can fill a tank in 18 minutes and 24 minutes respectively. Both the pipes are opened together but P left the work 3 minutes before filling the tank. Find the total time taken by both of them to fill the tank?
a) 12 min
b) 10 min
c) 14 min
d) 8 min
e) None of these
10) A bag contains (x + 2) violet, 4 red and 8 yellow color balls. If two balls are taken random and the probability of getting both red color balls is 2/51, then find the difference between the number of violet color balls and yellow color balls?
a) 3 balls
b) 4 balls
c) 1 ball
d) 2 balls
e) None of these
Answers :
Directions (1 – 5):
1/Neha = 1/20
1/Nitin + 1/Neha = 1/15
=> 1/Nitin + 1/20 = 1/15
=> 1/Nitin = 1/15 – 1/20
=> 1/Nitin = (4 – 3)/60
=>1/Nitin = 1/60
1/Meena = 1/30
1/Mukesh + 1/Meena = 1/18
=> 1/Mukesh + 1/30 = 1/18
=> 1/Mukesh = 1/18 – 1/30
=> 1/Mukesh = (5 – 3)/90
=> 1/Mukesh = 2/90
=>1/Mukesh = 1/45
1/Hena = 1/20
1/Harish + 1/Hena = 1/12
=> 1/Harish + 1/20 = 1/12
=> 1/Harish = 1/12 – 1/20
=> 1/Harish = (5 – 3)/60
=> 1/Harish = 2/60
=>1/Harish = 1/30
1/Deepa = 1/48
1/Dinesh + 1/Deepa = 1/16
=>1/Dinesh + 1/48 = 1/16
=> 1/Dinesh = 1/16 – 1/48
=> 1/Dinesh = (3 – 1)/48
=> 1/Dinesh = 2/48
=>1/Dinesh = 1/24
1/Seema = 1/60
1/Saurabh + 1/Seema = 1/22.5
=> 1/Saurabh + 1/60 = 10/225
=> 1/Saurabh = 2/45 – 1/60
=> 1/Saurabh = (8 – 3)/180
=> 1/Saurabh = 5/180
=>1/Saurabh = 1/36
1) Answer: b)
Sum of the efficiencies of Meena and Harish = 1/30 + 1/30
= 2/30
= 1/15
Sum of the efficiencies of Seema and Dinesh = 1/60 + 1/24
= (2 + 5)/120
= 7/120
Required ratio= 1/15: 7/120
= 8: 7
2) Answer: d)
Let, required time taken = t days
12/60 + t x (1/48 + 1/36) = 1
=> 1/5 + t x (3 + 4)/144 = 1
=> 7t/144 = 1 – 1/5
=> 7t/144 = (5 – 1)/5
=> t = 144/7 x 4/5
=> t = 576/35 days
3) Answer: e)
Let, time taken by Neha and Harish to complete the work together = t days
And time taken by Hena and Mukesh to complete the work together = n days
t x (1/20 + 1/30) = 1
=> t x (3 + 2)/60 = 1
=> t = 60/5
=> t = 12 days
n x (1/20 + 1/45) = 1
=> n x (9 + 4)/180 = 1
=> n = 180/13 days
Required percentage = 12/(180/13) x 100 = 86.67% = 87% approx.\
4) Answer: b)
Let, required time taken = t days
t x (1/60 + 1/30 + 1/20 + 1/30) = 1
=> t x (1 + 2 + 3 + 2)/60 = 1
=> t = 60/8
=> t = 15/2 days
5) Answer: d)
Let, required time = t days
12/36 + 12/24 + t x (1/36 + 1/24 + 1/60) = 1
=> 1/3 + ½ + t x (10 + 15 + 6)/360 = 1
=>31t/360 = 1 – 1/3 – ½
=> 31t/360 = (6 – 2 – 3)/6
=> t = 360/31 x 1/6
=> t = 60/31 days
Direction (6-10) :
6) Answer: a)
Let the present age of man and son be x and y respectively,
(x – 5) = 4 * (y – 5) + 7
x – 5 = 4y – 20 + 7
x – 4y = -8 –> (1)
(x + 3) = 3 * (y + 3) – 2
x + 3 = 3y + 9 – 2
x – 3y = 4 —> (2)
By solving the equation (1) and (2), we get,
x = 40, y = 12
Sum of the present age of man and his son = 40 + 12 = 52 years
After 19 years, the sum of their age = 52 + 38 = 90 years
7) Answer: a)
The share of A, B and C,
= > [4x * 4 + 4x * (150/100) * 8]: [5x * 6 + 5x * (3/5) * 6]: [8x * 12]
= > [16x + 48x]: [30x + 18x]: [96x]
= > 64x: 48x: 96x
= > 4: 3: 6
13’s = 98800
1’s = 7600
The share of C = 6’s = Rs. 45600
8) Answer: c)
Let the sum be x and the rate of interest be r %,
[(x * (r + 4) * 5) / 100] – [(x * r * 5)/100] = 6000(5xr/100) + (20x/100) – (5xr/100) = 6000
(20x/100) = 6000
x = (6000 * 100)/20 = Rs. 30000
9) Answer: a)
Let the total time taken by both of them to fill a tank be x,
(x – 3)/18 + x/24 = 1
(4x – 12 + 3x)/72 = 1
7x – 12 = 72
7x = 84
x = 12 min
10) Answer: d)
4C2 / (x+14)C2 = 2/51
[(4 * 3) / (1 * 2)] / [(x + 14) (x + 13) / (1 * 2)] = 2/51(51 * 6) = x2 + 13x + 14x + 182
306 = x2 + 27x + 182
x2 + 27x – 124 = 0
(x – 4) (x + 31) = 0
x = 4, -31 (negative value will be eliminated)
Required difference = 8 – 6 = 2 balls





