RRB Clerk Mains Quantitative Aptitude Questions 2021 (Day-04)

Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for IBPS RRB Clerk Mains 2021 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.

Click Here to – Get SBI PO Online Practice Mock Test

Start Quiz

Pie chart

Directions (1-5): Study the following information carefully and answer the questions given below.

The given pie chart shows the percentage of total employees (who like both tea and coffee) in six different companies.

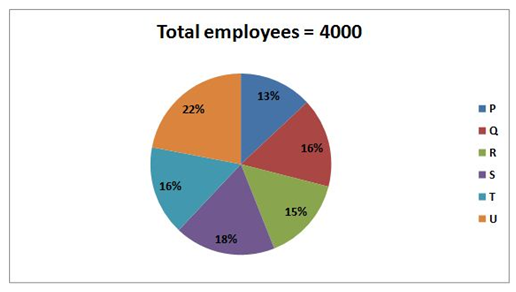
The given table shows the percentage of the employees who like coffee in six different companies.

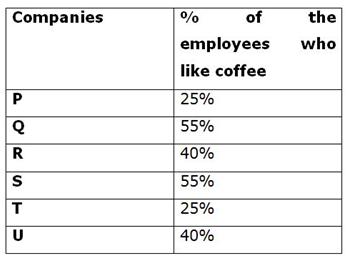
1) If four-fifth and three-fourth of the employees in S and U are male and the ratio of the number of male who like coffee to tea in S and U is 5:4 and 2:3 respectively, then what is the difference between the number of female employees who like tea in S and U together and the number of female employees who like coffee in S and U?

A.28

B.32

C.36

D.40

E.42

2) What is the ratio of the number of employees who like tea in P and R together to S and T together?

A.121:133

B.127:134

C.131:142

D.133:145

E.None of these

3) What is the approximate average number of employees who like coffee in all the companies together?

A.268

B.272

C.278

D.260

E.256

4) Average number of employees who like tea in all the companies together is what percent of the total number of employees in P, S and R together?

A.19.98%

B.21.46%

C.23.34%

D.17.78%

E.25.61%

5) If one-fourth of the employees in P like Apple juice and 15% of the employees in Q are like Apple juice, one-fifth of the employees in R are like apple juice and three-twenty employees in S are like Apple juice, then find the total number of employees in P, Q, R and S who like apple juice?

A.454

B.456

C.444

D.464

E.465

Quadratic equation

Directions (06-10): Following question contains two equations as I and II. You have to solve both equations and determine the relationship between them and give answer as,

6) I) x² – 44x + 468 =0

II) y²– 39y + 378=0

A.x > y

B.x ≥ y

C.x = y or relationship can’t be determined.

D.x < y

E.x ≤ y

7) I) x² + 27x + 162=0

II)2y²+ 42y + 216=0

A.x > y

B.x ≥ y

C.x = y or relationship can’t be determined.

D.x < y

E.x ≤ y

8) I) 3x² – 51x + 216=0

II) y²+ 19y – 66 =0

A.x > y

B.x ≥ y

C.x = y or relationship can’t be determined.

D.x < y

E.x ≤ y

9) I) x² – 10x – 504 =0

II) y²+ 40y + 396 =0

A.x > y

B.x ≥ y

C.x = y or relationship can’t be determined.

D.x < y

E.x ≤ y

10) I) x² + 275 = 396

II) y²– 23y + 132 =0

A.x > y

B.x ≥ y

C.x = y or relationship can’t be determined.

D.x < y

E.x ≤ y

Answers :

Directions (1-5) :

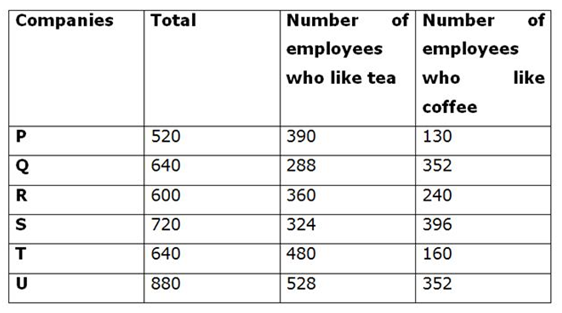
1) Answer: C

Number of male employees in S = 4/5 * 720 = 576

Number of male employees in U = 3/4 * 880 = 660

Number of male employees who like coffee in S = 5/9 * 576 = 320

Number of male employees who like tea in S = 4/9 * 576 = 256

Number of male employees who like coffee in U = 660 * 2/5 = 264

Number of male employees who like tea in U = 660 * 3/5 = 396

Number of female employees like tea in S = 324 – 256 = 68

Number of female employees like coffee in S = 396 – 320 = 76

Number of female employees like coffee in U = 352 – 264 = 88

Number of female employees like tea in U = 528 – 396 = 132

Difference = (132 + 68) – (76 + 88)

= 200 – 164

= 36

2) Answer: E

Required ratio = (390 + 360):(324 + 480)

= 750:804

= 125:134

3) Answer: B

Required average = (352 + 130 + 352 + 240 + 396 + 160)/6

= 1630/6

= 272

4) Answer: B

Required percentage = ((390 + 288 + 360 + 324 + 480 + 528)/6)/(520 + 600 + 720) * 100

=395*100/1840

= 21.46%

5) Answer: A

Number of employees like Apple juice in P =1/4 * 520 = 130

Number of employees like Apple juice in Q = 15/100 * 640 = 96

Number of employees like Apple juice in R = 1/5 * 600 = 120

Number of employees like Apple juice in S = 720 * 3/20 = 108

Required total = 130 + 96 + 120 + 108 = 454

6) Answer: C

x² – 44x + 468 = 0

x² – 26x – 18x + 468 = 0

x(x – 26) – 18(x – 26) = 0

(x – 18)(x – 26) = 0

x = 18, 26

y² – 39y + 378 = 0

y² – 21y – 18y + 378 = 0

y(y – 21) – 18(y – 21) = 0

(y – 18)(x – 21) = 0

y = 18, 21

Relationship between x and y cannot be established.

7) Answer: C

x² + 27x + 162 = 0

x² + 9x + 18x + 162 = 0

x(x + 9) + 18(x + 9) = 0

(x + 18)(x + 9) = 0

x = -18, -9

2y² + 42y + 216 = 0

2y² + 24y + 18y + 216 = 0

2y(y + 12) + 18(y + 12) = 0

(2y + 18)(y + 12) = 0

y = -9, -12

Relationship between x and y cannot be established.

8) Answer: A

3x² – 51x + 216 = 0

3x² – 24x – 27x + 216 = 0

3x(x – 8) – 27(x – 8) = 0

(3x – 27)(x – 8) = 0

x = 9, 8

y² + 19y – 66 = 0

y² + 22y – 3y – 66 = 0

y(y + 22) – 3(y + 22) = 0

(y – 3)(y + 22) = 0

y = 3, -22

x > y

9) Answer: B

x² – 10x – 504 = 0

x² – 28x + 18x – 504 = 0

x(x – 28) + 18(x – 28) = 0

(x + 18)(x – 28) = 0

x = -18, 28

y² + 40y + 396 = 0

y² + 18y + 22y + 396 = 0

y(y + 18) + 22(y + 18) = 0

(y + 22) (y + 18) = 0

y = -22, -18

x ≥ y

10) Answer: E

x² + 275 = 396

x² = 121

x = 11, -11

y² – 23y + 132 = 0

y² – 12y – 11y + 132 = 0

y(y – 12) – 11(y – 12) = 0

(y – 11)(y – 12) = 0

y = 11, 12

x ≤ y