Dear Aspirants,
Mathematics is a complex web. So only most of the applicant’s thought is RRB Mathematics questions are tough to work out. It’s really not, to score the maximum mark in this section you need of regular practice on RRB JE Maths every day.
Start to practice Quiz for RRB Mathematics section and reveal the answers with detailed explanation. We have taken much care on the explanation part that to understand the RRB Mathematics questions easily. Take RRB Mathematics quiz regularly to perform better on RRB JE Maths section without any hurdle.
[WpProQuiz 5086]Click here to View Mathematics Questions in Hindi
1) Find the greatest 5 digit number which is divisible by 35?
a) 99995
b) 99990
c) 99985
d) 99980
2) What is the least number added to 5200 to get a number exactly divisible by 180?
a) 180
b) 160
c) 20
d) 60
3) If two-fifth of two-third of one-third of a number is 16, find the number?
a) 60
b) 180
c) 280
d) 90
4) A certain number consist of two digit number whose sum is 9. If the order of digit is reversed, the new number is 9 less than the original number. What is the original number?
a) 45
b) 36
c) 54
d) 63
5) How many numbers up to 300 is divisible by 5 and 7 together?
a) 9
b) 10
c) 7
d) 8
6) The difference between the squares of two consecutive numbers is 39. What are the numbers?
a) 19,20
b) 20, 21
c) 18,19
d) 17,18
7) When a number is added to another number the total become 250% of the second number. What is the ratio between the first and the second number?
a) 3 : 2
b) 2 : 3
c) 4 : 3
d) 3 : 4
8) The sum of three consecutive odd numbers is equal to one-fourth of 156.what is the middle number?
a) 8
b) 10
c) 12
d) 13
9) A positive number which is when decreased by 4 is equal to 21 times the reciprocal of the same number. Find the number?
a) 3
b) 4
c) 7
d) 5
10) A number when divided by 1404, leave a remainder 93. What remainder would be obtained by dividing the same by 39?
a) 39
b) 29
c) 21
d) 15
Answers :
1) Answer: a)
Greatest 5 digit no = 99999
By dividing 999999 by 35 remainder = 4
So greatest 5 digit number divisible by 35 = 99999 – 4 = 99995
2) Answer: c)
After dividing 5200 by 180 Remainder =160
Required Number to be added = 180 – 160 = 20
3) Answer: b)
2/5×2/3×1/3 × Number = 16
X = 16×5×3×3/2×2 = 180
4) Answer: c)
Let the number be 10x + y
x + y =9
(10x + y) – (10y + x) = 9
x – y = 1
By solving these two we get x= 5 and y=4
5) Answer: d)
LCM of 5 and 7 = 35
300 = 8 × 35 +20
So number which are divided by 5 and 7 together is 8
6) Answer: a)
The 1st number = x
Consecutive next number = x + 1
x2 – (x + 1)2 = 39
x2 – x2 + 1 – 2x = 39
1 – 2x = 39
x = 19
The numbers are 19, 20
Alternate method
(Number +1)/2 = 40/2 = 20
(Number – 1)/2 = 38/2 = 19
7) Answer: a)
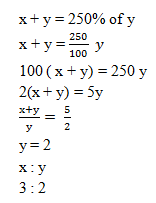
8) Answer: d)
x + x + 2 + x + 4 = ¼ × 156
3x + 6 = 39
3x = 33
x = 11
x + 2 = 13
The middle value of the number = 13
9) Answer: c)
x – 4 = 21(1/x)
x2 – 4x = 21
x2 – 4x – 21 = 0
Solving this equation
x2 + 3x – 7x – 21 = 0
x (x + 3) – 7 ( x + 3) = 0
(x – 7) (x + 3) = 0
So we get
x = 7 , – 4
Hence the positive number = 7
10) Answer: d)
Number = 140 × quotient + 93
= 39 × 6 × quotient + 39 × 2 + 15
Here 15 is remainder.






