SBI Clerk Prelims 2021 Quantitative Aptitude Questions (Day-28)

Dear Aspirants, Our IBPS Guide team is providing new series of Quantitative Aptitude Questions for SBI Clerk Prelims 2020 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these new series questions daily to familiarize with the exact exam pattern and make your preparation effective.

Start Quiz

Quadratic equation

Directions (01-05): Following question contains two equations as I and II. You have to solve both equations and determine the relationship between them and give answer as,

a)If x > y

b)If x ≥ y

c)If x = y or relationship cannot be determined.

d)If x < y

e)If x ≤ y

1) I) 2x² + 24x + 54 =0

II) 3y²– 21y+ 36 = 0

2) I) 3x² + 12x – 63 =0

II) y²– 16y + 63 = 0

3) I) (x + 2)² = 9

II) y^{2 =} 25

4) I) 1/x² × √x = 1/(2)³

II) y² – 7y + 12 = 0

5) I) x = √841

II) y²= 961

missing number series

Directions (6-10): Find out the missing number in the following number series.

6) 1, 9, 21, ?, 63, 93    

A.39

B.42

C.37

D.41

E.None of these

7) 342, ?, 210, 156, 110

A.306

B.272

C.240

D.281

E.None of these

8) 1, 5/2, 5, ?, 13, 37/2, 25

A.21/2

B.19/2

C.17/2

D.23/2

E.None of these

9) 3, 3, 4.5, 11.25, 45, 270, ?

A.2250

B.2285

C.2295

D.2025

E.None of these

10) 1.42, 1.94, 2.54, ?, 3.98, 4.82

A.2.23

B.3.22

C.2.77

D.3.24

E.None of these

Answers :

1) Answer: D

2x² + 18x + 6x + 54 =0

2x(x + 9) + 6 (x + 9) = 0

(2x + 6) (x + 9) = 0

Roots, x = – 9, -3

3y² – 21y + 36 = 0

3y² – 12y – 9y + 36 = 0

3y (y – 4) – 9(y- 4) = 0

(3y – 9) (y – 4) = 0

Roots, y =  4, 3

Hence, x < y

2) Answer: D

3x² + 12x – 63 = 0

3x² + 21x – 9x – 63 = 0

3x(x + 7) – 9(x + 7) = 0

(x + 7) (3x – 9) = 0

Roots, x = -7, 3

y² – 16y + 63 = 0

y² – 9y – 7y + 63 = 0

y(y – 9) – 7(y – 9) = 0

(y – 9) (y – 7) = 0

y = 9, 7

Hence, x < y

3) Answer: C

x² + 4x + 4 = 9

x² + 4x – 5 = 0

x² + 5x – x – 5 = 0

x(x + 5) – 1(x + 5) =0

(x + 5) (x – 1) = 0

Roots, x= -5, 1

y^{2 =} 25

Roots, y = 5, – 5

Hence, relationship cannot be determined.

4) Answer: B

1/x² × √x = 1/(2)³

x^-2 × x^1/2 = 1/(√4)³

x^-3/2 = 1/(4^1/2)³

x^-3/2 = 1/(4)^3/2

x^-3/2 = (4)^-3/2

x = 4

 y² – 7y + 12 = 0

y² – 4y – 3y + 12 = 0

y(y – 4) – 3 (y – 4) =0

(y – 4)(y – 3) = 0

Roots, y = 4, 3

Hence, x ≥ y

5) Answer: C

x = √841

x = 29

y² = 961

y = +31, – 31

Hence, relationship can’t be determined

6) Answer: A

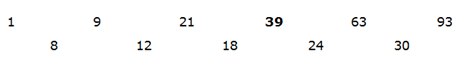
3 + 5 = 8 (sum of prime numbers)

5 + 7 = 12

7 + 11 = 18

11 + 13 = 24

13 + 17 = 30

Therefore, 21 + 18 = 39

7) Answer: B

19² – 19 = 342

17² – 17 = 272

15² – 15 = 210

13² – 13 = 156

11² – 11 = 110

8) Answer: C

1 + 3/2 = 5/2

5/2 + 5/2 = 5

5 + 7/2 = 17/2

17/2 + 9/2 = 13

13 + 11/2 = 37/2

37/2 + 13/2 = 25

9) Answer: C

(3 × 1) = 3

(3 × 1.5) = 4.5

(4.5 × 2.5) = 11.25

(11.25 × 4) = 45

(45 × 6) = 270

(270 × 8.5) = 2295

10) Answer: B

Check Here to View SBI Clerk Prelims 2021 Quantitative Aptitude Questions
Day – 27	Day – 26	Day – 25