SBI PO 2019 Notification will be expected soon. It is one of the most expected recruitment among the banking aspirants. Every year the exam pattern for SBI PO has been changing. Depends upon the changing of exam pattern the questions are quite harder compare to the previous year. So the questions are in high level than the candidate’s assumption.
As per the latest trend, our IBPS Guide is providing the updated New Exam Pattern Quantitative Aptitude questions for SBI PO 2019 Day 9. Our Skilled experts were mounting the questions based on the aspirant’s needs. So candidates shall start your preparation and practice on daily basis with our SBI PO pattern quantitative aptitude questions 2019 day 9. Start your effective preparation from the right beginning to get success in upcoming SBI PO 2019.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5092]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
1) A, B and C started a business by investing Rs. 45000, Rs. 32000 and Rs. ______ respectively. After 5 months, A withdraws Rs. 15000 and B invested Rs. ______ more. And after another 3 months, C invested 25 % of initial investment more. The ratio of share of A, B and C, at the end of the year is 435: 440: 364.
Which of the following options satisfy the given condition?
a) 22000, 6000
b) 24000, 10000
c) 28000, 8000
d) 26000, 4000
e) 30000, 5000
2) A shopkeeper allowed ____ % discount on an item on the marked price and he suffered a loss of _____ %. If he allows only 10% discount, then the profit percentage would be 8 %.
Which of the following options satisfy the given condition?
a) 30, 10
b) 25, 15
c) 35, 22
d) 25, 10
e) Both c) and d)
3) The difference between Simple interest and Compound interest on a certain sum at the rate of _____% per annum for two years is Rs. _____. The simple interest on the same sum at the rate of 15% per annum for 5 years is Rs. 33750?
Which of the following options satisfy the given condition?
I) 12, 648
II) 10, 450
III) 15, 956
a) Only I
b) Only II
c) Only III
d) Both I and II
e) Both II and III
4) ____ litres of mixture of milk and water contains milk and water in the ratio of 3 : 2. The ____ litres of water should be added to the mixture to get 45 % milk on it.
Which of the following options satisfy the given condition?
I) 75, 25
II) 90, 30
III) 100, 24
a) Only I
b) Only II
c) Only III
d) Both II and III
e) Both I and II
5) The average weight of _____ persons is increased by 3 when one of the person whose weight is 58 kg replaced by 2 women. The average weight of 2 women is _____ kg.
Which of the following options satisfy the given condition?
a) 16, 52
b) 14, 48
c) 12, 47
d) 18, 58
e) None of these
Directions (Q. 6 – 10): Study the following information carefully and answer the given questions.
The following bar graph-1 shows the total clothes (Indian and Western) in 6 different shops and the bar graph-2 shows the total Western clothes in the shops.
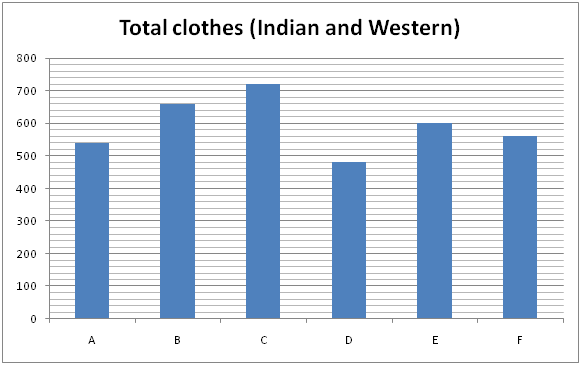
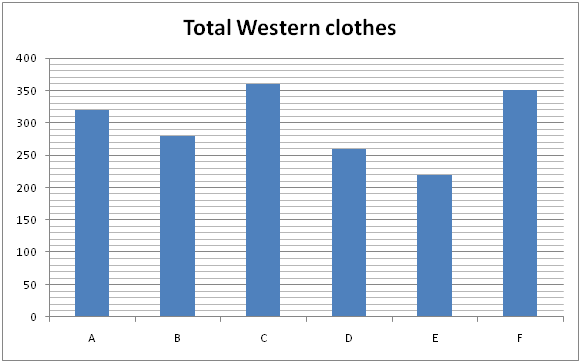
6) Find the ratio between the total clothes (Indian and Western) in shop A and C together to that of total western clothes in shop B and D together?
a) 7: 3
b) 12: 5
c) 19: 11
d) 23: 15
e) None of these
7) Find the average western clothes in shop A, C and E together?
a) 240
b) 280
c) 320
d) 300
e) None of these
8) Total Indian clothes in shop A and B together is approximately what percentage of total western clothes in shop B and F together?
a) 108 %
b) 95 %
c) 82 %
d) 74 %
e) 126 %
9) Find the difference between the average number of clothes in shop A and F together to that of the average number of Indian clothes in shop C and E together?
a) 180
b) 220
c) 150
d) 90
e) None of these
10) Total Western clothes in shop B and C together is approximately what percentage less than the total clothes (Indian and Western) in shop A and D together?
a) 23 %
b) 44 %
c) 37 %
d) 52 %
e) 66 %
Answers :
1) Answer: c)
Option (a)
The share of A, B and C
= > [45000*5 + 30000*7]: [32000*5 + 38000*7]: [22000*8 + 22000*(125/100)*4]
= > [225000 + 210000]: [160000 + 266000]: [176000 + 110000]
= > 435000: 426000: 286000
= > 435: 426: 286 ≠ 435: 440: 364
This option doesn’t satisfy the given condition
Option (b)
The share of A, B and C
= > [45000*5 + 30000*7]: [32000*5 + 42000*7]: [24000*8 + 24000*(125/100)*4]
= > [225000 + 210000]: [160000 + 294000]: [192000 + 120000]
= > 435000: 454000: 312000
= > 435: 454: 312 ≠ 435: 440: 364
This option doesn’t satisfy the given condition
Option (c)
The share of A, B and C
= > [45000*5 + 30000*7]: [32000*5 + 40000*7]: [28000*8 + 28000*(125/100)*4]
= > [225000 + 210000]: [160000 + 280000]: [224000 + 140000]
= > 435000: 440000: 364000
= > 435: 440: 364
This option satisfy the given condition
Option (d)
The share of A, B and C
= > [45000*5 + 30000*7]: [32000*5 + 36000*7]: [26000*8 + 26000*(125/100)*4]
= > [225000 + 210000]: [160000 + 252000]: [208000 + 130000]
= > 435000: 412000: 338000
= > 435: 412: 338 ≠ 435: 440: 364
This option doesn’t satisfy the given condition
Option (e)
The share of A, B and C
= > [45000*5 + 30000*7]: [32000*5 + 37000*7]: [30000*8 + 30000*(125/100)*4]
= > [225000 + 210000]: [160000 + 259000]: [240000 + 150000]
= > 435000: 419000: 390000
= > 435: 419: 390 ≠ 435: 440: 364
This option doesn’t satisfy the given condition
2) Answer: d)
Option (a)
Let the marked price be x,
Selling price = x*(70/100) = 7x/10
Cost price = (7x/10) * (100/90) = 7x/9
When 10% discount is allowed,
Selling price = x*(90/100) = 9x/10
Profit = (9x/10) – (7x/9)
= > (81x – 70x)/90
= > 11x/90
Profit percentage = [(11x/90) / (7x/9)]*100
= (11x/90) * (9/7x) * 100
= 15.7 %
This option doesn’t satisfy the given condition
Option (b)
Let the marked price be x,
Selling price = x*(75/100) = 3x/4
Cost price = (3x/4) * (100/85) = 15x/17
When 10% discount is allowed,
Selling price = x*(90/100) = 9x/10
Profit = (9x/10) – (15x/17)
= > (153x – 150x)/170
= > 3x/170
Profit percentage
= > [(3x/170) / (15x/17)]*100 = (3x/170) * (17/15x) * 100 = 2 %
This option doesn’t satisfy the given condition
Option (c)
Let the marked price be x,
Selling price = x*(65/100) = 13x/20
Cost price = (13x/20) * (100/78) = 5x/6
When 10% discount is allowed,
Selling price = x*(90/100) = 9x/10
Profit = (9x/10 – 5x/6)
= (27x – 25x)/30 = 2x/30
= x/15
Profit % = (x/15)/(5x/6) * 100
= 8%
This option satisfy the given condition
Option (d)
Let the marked price be x,
Selling price = x*(75/100) = 3x/4
Cost price = (3x/4) * (100/90) = 5x/6
When 10% discount is allowed,
Selling price = x*(90/100) = 9x/10
Profit = (9x/10) – (5x/6)
= > (54x – 50x)/60
= > 4x/60 = x/15
Profit percentage = [(x/15) / (5x/6)]*100 = (x/15) * (6/5x) * 100 = 8 %
This option satisfy the given condition
3) Answer: d)
SI = (P*n*r)/100
33750 = (P*5*15)/100
P = (33750*100)/75 = Rs. 45000
Option (a)
The difference between CI and SI for two years is,
Diff = P*(r/100)2
= > 45000*(12/100)2
= > 45000*(144/10000) = Rs. 648
This option satisfies the given condition.
Option (b)
The difference between CI and SI for two years is,
Diff = P*(r/100)2
= > 45000*(10/100)2
= > 45000*(1/100) = Rs. 450
This option satisfies the given condition.
Option (c)
The difference between CI and SI for two years is,
Diff = P*(r/100)2
= > 45000*(15/100)2
= > 45000*(/10000) = Rs. 1012.5
This option doesn’t satisfy the given condition.
4) Answer: e)
Option (a)
Total mixture of milk and water = 75 litres
5’s = 75
1’s = 15
Total milk = 45 litres, water = 30 litres
According to the question,
45/(30 + x) = (45/55)
45/(30 + x) = 9/11
55 = 30 + x
X = 25
25 litres of water should be added to the mixture.
This option satisfies the given condition.
Option (b)
Total mixture of milk and water = 90 litres
5’s = 90
1’s = 18
Total milk = 54 litres, water = 36 litres
According to the question,
54/(36 + x) = (45/55)
54/(36 + x) = 9/11
66 = 36 + x
X = 30
30 litres of water should be added to the mixture.
This option satisfies the given condition.
Option (c)
Total mixture of milk and water = 100 litres
5’s = 100
1’s = 20
Total milk = 60 litres, water = 40 litres
According to the question,
60/(40 + x) = (45/55)
60/(40 + x) = 9/11
220 = 120 + 3x
100 = 3x
X = 100/3 = 33.33 litres
33.33 litres of water should be added to the mixture.
This option doesn’t satisfy the given condition.
5) Answer: c)
Option (a)
Increased weight = 16*3 = 48 kg
So 2 women’s weight = 58 kg + 48 kg = 106 kg
Average weight of 2 women = 106/2 = 53 kg
This option doesn’t satisfy the given condition.
Option (b)
Increased weight = 14*3 = 42 kg
So 2 women’s weight = 58 kg + 42 kg = 100 kg
Average weight of 2 women = 100/2 = 50 kg
This option doesn’t satisfy the given condition.
Option (c)
Increased weight = 12*3 = 36 kg
So 2 women’s weight = 58 kg + 36 kg = 94 kg
Average weight of 2 women = 94/2 = 47 kg
This option satisfies the given condition.
Option (d)
Increased weight = 18*3 = 54 kg
So 2 women’s weight = 58 kg + 54 kg = 94 kg
Average weight of 2 women = 112/2 = 56 kg
This option doesn’t satisfy the given condition.
Direction (6-10) :
6) Answer: a)
The total clothes (Indian and Western) in shop A and C together
= > 540 + 720 = 1260
The total western clothes in shop B and D together
= > 280 + 260 = 540
Required ratio = 1260: 540 = 7: 3
7) Answer: d)
The total western clothes in shop A, C and E together
= > 320 + 360 + 220 = 900
Required average = 900/3 = 300
8) Answer: b)
Total Indian clothes in shop A and B together
= > (540 – 320) + (660 – 280)
= > 220 + 380 = 600
Total western clothes in shop B and F together
= > 280 + 350 = 630
Required % = (600/630)*100 = 95 %
7) Answer: a)
The average number of clothes (Indian and Western) in shop A and F together
= > (540 + 560)/2 = 550
The total number of Indian clothes in shops C and E together
= > (720 – 360) + (600 – 220)
= > 360 + 380 = 740
The average number of Indian clothes in shops C and E together
= > 740/2 = 370
Required difference = 550 – 370 = 180
10) Answer: c)
Total Western clothes in shop B and C together
= > 280 + 360 = 640
Total clothes (Indian and Western) in shop A and D together
= > 540 + 480 = 1020
Required % = [(1020 – 640)/1020]*100 = (380/1020)*100 = 37 %





