SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5287]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Read the following information carefully and answer the given questions.
There are two friends A and B, playing different games consisting of dices and cards. There are five types of game (i.e.) game 1, game 2, game 3, game 4 and game 5. In game 1, both of them are allowed to throw a dice alternatively. If more than 5 appear on throwing, the person is said to be the winner. In game 2, they throw a pair of dice alternatively. A wins if he gets a sum of 9 before B gets a sum of 10 and B wins if he gets a sum of 10 before A gets a sum of 9. In game 3, both of them are allowed to throw a card from a well shuffled deck of 52 cards without replacement. Any person said to win this game, if he throws a number card. In game 4, both of them are allowed to throw a pair of dice alternatively. A wins if he gets a multiple of 6 before B gets a multiple of 8 and B wins if he gets a multiple of 8 before A gets a multiple of 6. In game 5, both of them are allowed to throw a card from a well shuffled deck of 52 cards without replacement. Any person said to win this game, if he throws a letter card.
1) If B begins game 4, find the probability of B’s winning in his third attempt.
a) 225/5832
b) 321/5832
c) 289/5832
d) 361/5832
e) None of these
2) If A starts the game 2, find the probability of A’s winning in his second attempt.
a) 7/81
b) 8/81
c) 11/81
d) 13/81
e) 19/81
3) If A begins the game 1, find the probability of A’s winning in his third attempt.
a) 125/216
b) 25/36
c) 5/216
d) 25/216
e) None of these
4) If A begins the game 3, find the probability of A’s winning in his third attempt.
a) 196/2197
b) 154/2197
c) 121/2197
d) 144/2197
e) None of these
5) If A begins the game 5, find the probability of A’s winning in his third attempt.
a) 216/2197
b) 288/2197
c) 252/2197
d) 361/2197
e) None of these
Directions (6 – 10): Study the following graph carefully and answer the given questions.
Number of staff in an office in different department is shown in the line graph.
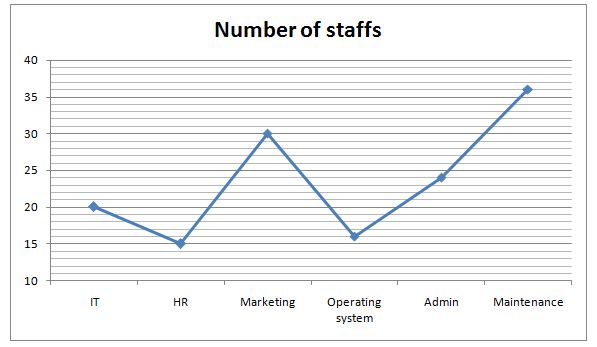
6) A team of 5 members of IT, HR and Admin department member is to be formed for a project, find the number of ways in which the team can be formed, if the team does not have 2 members of same department except Admin department?
a) 652050
b) 687900
c) 989820
d) 607200
e) None of these
7) In how many ways, a team of 4 members can be formed so that two particular IT staffs are always there in the team?
a) 6870
b) 6980
c) 7290
d) 9870
e) None of these
8) A team of 5 members is to be formed with IT and Marketing staff. Find the number of ways to do so such that the team has at least 1 member of each department?
a) 1879500
b) 1988820
c) 1960750
d) 2168910
e) None of these
9) A team of 5 members is to be formed for a project such that the team has at least one member of each department excluding Operating system. In how many ways it can be done?
a) 7776000
b) 7767000
c) 8977000
d) 8979400
e) 6988900
10) If 6 Admin department staff’s and 6 Operating system department staff’s are to be seated in a row of seats (numbered 1 – 12), then how many ways they can be seated if Admin department staff’s occupy even numbered seats only?
a) 1440
b) 5040
c) 1296
d) 720
e) None of these
Answers:
Directions (1-5):
1) Answer: c)
Total sample space = 62 = 36

Total possibilities of getting multiple of 6 = (1,6), (2,3), (3,2), (6,1) = 4
Total possibilities of getting multiple of 8 = (2,4), (4,2)
A’s winning probability = 4/36 = 1/9
A’s losing probability = (36-4)/36 = 32/36 = 8/9
B’s winning probability = 2/36 = 1/18
B’s losing probability = (36-2)/36
= 34/36 = 17/18
Probability of B winning in his 3rd attempt
= 17/18*17/18*1/18
= 289/5832
2) Answer: b)
Total sample space = 62 = 36

Total possibilities of getting a sum of 9 = (3,6), (4,5), (5,4), (6,3) = 4
Total possibilities of getting a sum of 10 = (4,6), (5,5), (6,4) = 3
A’s winning probability = 4/36 = 1/9
A’s losing probability = 1 – 1/9 = 8/9
B’s winning probability = 3/36 = 1/12
B’s losing probability = 1 – 1/12 = 11/12
Probability of A winning in his 2nd attempt
= 8/9*1/9 = 8/81
3) Answer: d)
Total sample space = 61 = 6 = (1, 2, 3, 4, 5, 6)
In game 1, both of them are allowed to throw a dice alternatively. If more than 5 appear on throwing, the person is said to be the winner.
Winning probability = 1/6
Losing probability = 5/6
Probability of A winning in his 3rd attempt
= 5/6*5/6*1/6
= 25/216
4) Answer: d)
Total cards = 52
Total number cards = 9*4 = 36
Total face card = 3*4 = 12
Total letter card = 4*4 = 16
A’s winning probability = 36/52
= 9/13
A’s losing probability = (52-36)/52
= 16/52 = 4/13
Probability of A’s winning in his third attempt
= 4/13*4/13*9/13
=144/2197
5) Answer: e)
Total cards = 52
Total number cards = 9*4 = 36
Total face card = 3*4 = 12
Total letter card = 4*4 = 16
A’s winning probability = 16/52
= 4/13
A’s losing probability = 1 – 4/13
= 9/13
Probability of A winning in his 3rd attempt
= 9/13 * 9/13 * 4/13
= 324/2197
Directions (6-10):
6) Answer: d)
Number of ways = 20C1*15C1*24C3
= 20*15*(24*23*22/1*2*3)
= 607200
7) Answer: d)
Number of ways = (20+15+30+16+24+36)C(4 – 2)
= 141C2
= (141*140)/(1*2)
= 9870
8) Answer: c)
Required probability
= (20C1*30C4 + 20C2*30C3 + 20C3*30C2 + 20C4*30C1)
= [(20*(30*29*28*27/1*2*3*4)) + ((20*19/1*2)*(30*29*28/1*2*3)) + ((20*19*18/1*2*3)*(30*29/1*2)) + ((20*19*18*17/1*2*3*4)*30)
= (25*29*28*27) + (190*5*29*28) + (20*19*3*15*29) + (5*19*3*17*30)
= 548100 + 771400 + 495900 + 145350
= 1960750
9) Answer: a)
Required number of ways = 20C1*15C1*30C1*24C1*36C1
= 20*15*30*24*36
= 77760000
10) Answer: e)
Required number of ways = 6! * 6!
= 6*5*4*3*2*1 * 6*5*4*3*2*1
= 720*720
= 518400





