SBI PO 2019 Notification is about to come and it is the most awaited exam among the aspirants. We all know that new pattern questions are introducing every year in the SBI PO exam. Further, the questions are getting tougher and beyond the level of the candidate’s expectations.
Our IBPS Guide is providing High-Level New Pattern Quantitative Aptitude Questions for SBI PO 2019 so the aspirants can practice it on a daily basis. These questions are framed by our skilled experts after understanding your needs thoroughly. Aspirants can practice these high-level questions daily to familiarize with the exact exam pattern. We wish that your rigorous preparation leads you to a successful target of becoming SBI PO.
“Be not afraid of growing slowly; be afraid only of standing still”
[WpProQuiz 5392]
Click Here for SBI PO Pre 2019 High-Quality Mocks Exactly on SBI Standard
Click Here to View Quantitative Aptitude Questions in Hindi
Directions (1 – 5): Study the following information carefully and answer the questions given below:
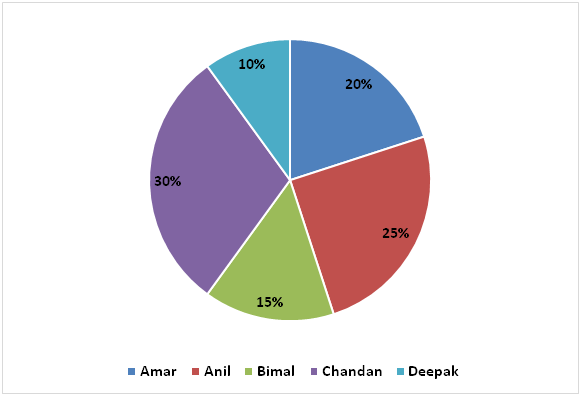
The first pie chart represents percentage wise distribution of amounts invested by five persons on simple interest.
Total amount invested by five persons on SI = Rs. 400000
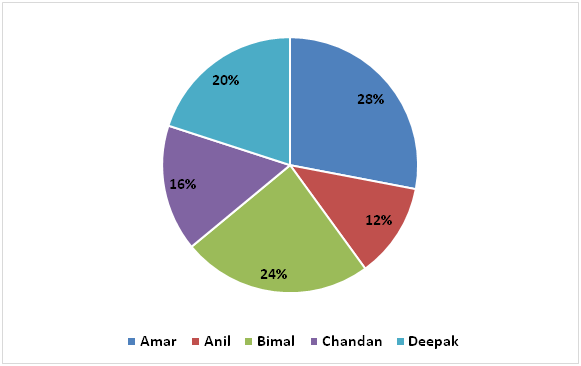
The second pie chart represents percentage wise distribution of amounts invested by five persons on compound interest.
Total amount invested by five persons on CI = Rs. 600000
1) The amount invested by Anil on simple interest at 8% per annum for four years. Then the amount invested by him on compound interest at 5% per annum for two years. The amount invested by Chandan on simple interest at 10% per annum for eight years. Find the respective ratio of the total interest earned by Anil from the amounts invested on simple interest and compound interest together and interest earned by Chandan from the amount invested on simple interest?
a) 1581 : 1987
b) 2101 : 3903
c) 1969 : 4800
d) 1768 : 3500
e) None of these
2) Amar invested his amount on compound interest at 6% per annum for three years and Deepak invested his amount on compound interest at 10% per annum for four years. Total amount received by Amar while investing on compound interest is approximately what percent of the total amount received by Deepak while investing on compound interest?
a) 130 %
b) 150 %
c) 115 %
d) 95 %
e) 80 %
3) The half of the amount invested by Bimal on simple interest is invested in scheme A which offers interest at 8% per annum for three years and that of the remaining half on scheme B at 6% per annum for six years. The amount invested by him on compound interest at 4% per annum for two years. Find the total interest earned by Bimal?
a) Rs.28560.4
b) Rs.29750.4
c) Rs.22050.8
d) Rs.24860.6
e) None of these
4) Find the relation between the following two quantities:
Quantity I: The amount invested by Chandan on compound interest is invested in scheme Y for 2 years and he received total amount of Rs.120422.4 at the end of two years. Find the rate of interest offered by scheme Y.
Quantity II: The one fourth of the amount invested by Amar on simple interest is invested in scheme X for five years and earned an interest of Rs.15000 at the end of five years. Find the rate of interest offered by scheme X.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II or no relation can be established.
5) Find the total interest earned by Keshav from the amount invested on compound interest.
Statement I: Amount invested by Keshav on compound interest is 20% more than the amount invested by Deepak on simple interest.
Statement II: Keshav invested his amount on compound interest for two years at 5% per annum.
a) Statement I alone is sufficient to answer the question, but the statement II alone is not sufficient.
b) Statement II alone is sufficient to answer the question, but the statement I alone is not sufficient.
c) Either statement I alone or statement II alone is sufficient to answer the question.
d) Both statements I and II together are needed to answer the question.
e) Both statements I and II together are not sufficient to answer the question.
Directions (6 – 10): Study the following information carefully and answer the questions given below:
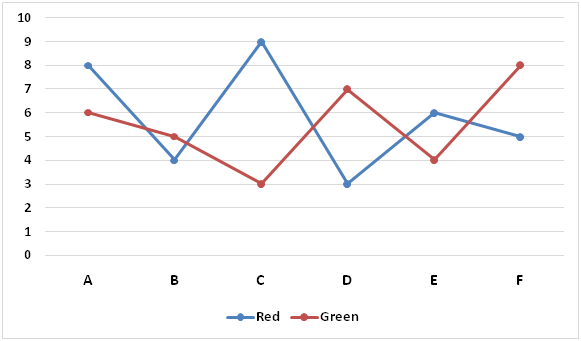
There are six bags, each contains balls of four different colours viz. Red, Green, Yellow and Blue.
The following line graph represents number of Red and Green balls in six bags.
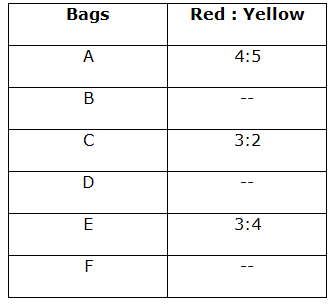
The following table represents respective ratio of number of Red balls and number of Yellow balls in six bags.
6) Probability of drawing one Blue ball from bag A is 1/7 and probability of drawing one Blue ball from bag C is 1/10. Probability of drawing two Red balls and two Blue balls from bag A is approximately what percent of the probability of drawing two Green balls and two Yellow balls from bag C?
a) 93%
b) 79%
c) 103%
d) 88%
e) 65%
7) Probability of drawing one Yellow ball from bag B is 1/6 and probability of drawing one Red ball from bag B is 2/9. Probability of drawing one Blue ball from bag E is 2/11. Find the respective ratio of total number of balls in bag B and total number of balls in bag E.
a) 7 : 9
b) 8 : 13
c) 9 : 11
d) 5 : 9
e) None of these
8) Probability of drawing one Blue ball from bag D is 3/10 and probability of drawing one Yellow ball from bag D is 1/5. Find the sum of the probability of drawing four balls from bag D such that all the balls are of different colour and probability of drawing four balls from bag D such that all the balls are of same colour.
a) 31/451
b) 39/335
c) 37/323
d) 35/321
e) None of these
9) Find the relation between following two quantities:
Quantity I: Probability of drawing one Yellow ball from bag C is ¼. Find the probability of drawing 2 Red, 1 Green and 1 Blue ball from bag C.
Quantity II: Probability of drawing one Green ball from bag E is 2/11. Find the probability of drawing 1 Red, 1 Green and 2 Blue balls from bag E.
a) Quantity I > Quantity II
b) Quantity I < Quantity II
c) Quantity I ≥ Quantity II
d) Quantity I ≤ Quantity II
e) Quantity I = Quantity II or no relation can be established.
10) Find the probability of drawing 2 Green balls and 2 Blue balls from bag F?
Statement I: Probability of drawing one Red ball from bag F is ¼ and probability of drawing one Yellow ball from bag F is 3/20.
Statement II: Probability of drawing one Green ball from bag F is 2/5 and probability of drawing one Blue ball from bag F is 1/5.
a) Statement I alone is sufficient to answer the question, but the statement II alone is not sufficient.
b) Statement II alone is sufficient to answer the question, but the statement I alone is not sufficient.
c) Either statement I alone or statement II alone is sufficient to answer the question.
d) Both statements I and II together are needed to answer the question.
e) Both statements I and II together are not sufficient to answer the question.
Answers :
Direction (1-5) :
1) Answer: c)
We know that
SI = (P x r x t)/100
CI = P x (1 + r/100)t – P
Amount invested by Anil on SI = 25/100 x 400000 = Rs.100000
Amount invested by Anil on CI = 12/100 x 600000 = Rs.72000
Amount invested by Chandan on SI = 30/100 x 400000 = Rs.120000
SI for Anil = (100000 x 8 x 4)/100 = Rs.32000
CI for Anil = 72000 x (1 + 5/100)2 – 72000
= 72000 x 105/100 x 105/100 – 72000
= 79380 – 72000
= Rs.7380
SI for Chandan = (120000 x 10 x 8)/100 = Rs.96000
Required ratio = (32000 + 7380) : 96000
= 39380 : 96000
= 1969 : 4800
2) Answer: c)
We know that,
Amount on CI = P x (1 + r/100)t
Amount invested by Amar on CI = 28/100 x 600000 = Rs.168000
Amount invested by Deepak on CI = 20/100 x 600000 = Rs.120000
Amount of Amar = 168000 x (1 + 6/100)3
= 168000 x 106/100 x 106/100 x 106/100
= Rs.200090.688
Amount of Deepak = 120000 x (1 + 10/100)4
= 120000 x 110/100 x 110/100 x 110/100 x 110/100
= Rs.175692
Required percentage = (200090.688/175692) x 100
= > 113.887% = 115%
3) Answer: b)
We know that
SI = (P x r x t)/100
CI = P x (1 + r/100)t – P
Amount invested by Bimal on SI = 15/100 x 400000 = Rs.60000
Amount invested by Bimal on CI = 24/100 x 600000 = Rs.144000
SI from scheme A = (30000 x 8 x 3)/100 = Rs.7200
SI from scheme B = (30000 x 6 x 6)/100 = Rs.10800
CI = 144000 x (1 + 4/100)2 – 144000
= 144000 x 104/100 x 104/100 – 144000
= 155750.4 – 144000
= Rs.11750.4
Total interest = 7200 + 10800 + 11750.4 = Rs.29750.4
4) Answer: b)
Quantity I:
We know that
Amount on CI = P x (1 + r/100)t
Amount invested by Chandan on CI = 16/100 x 600000 = Rs.96000
=> 120422.4 = 96000 x (1 + r/100)2
=> 120422.4/96000 = (1 + r/100)2
=>784/625 = (1 + r/100)2
=> (28/25)2 = (1 + r/100)2
=> 28/25 = 1 + r/100
=> r/100 = (28/25) – 1
=> r/100 = (28 – 25)/25
=> r = 100 x 3/25
=> r = 12%
Quantity II:
We know that
SI = (P x r x t)/100
Amount invested by Amar on simple interest = 20/100 x 400000 = Rs.80000
=> 15000 = (20000 x r x 5)/100
=> 1500000 = 100000 x r
=> r = 1500000/100000
=> r = 15%
Hence, Quantity I < Quantity II
5) Answer: d)
We know that
CI = P*[(1 + r/100)t – 1]
From I:
Amount invested by Deepak on simple interest
= 10/100 x 400000 = Rs. 40000
Amount invested by Keshav on compound interest
= 40000 x 120/100 = Rs. 48000
From II:
t = 2 years
r = 5%
From I and II:
CI = 48000 x (1 + 5/100)2 – 48000
= 48000 x 105/100 x 105/100 – 48000
= 52920 – 48000
= Rs. 4920
Hence, both the statements I and II together are needed to answer the question.
Direction (6-10) :
6) Answer: d)
In bag A:
Red = 8
Green = 6
Yellow = 5/4 x 8 = 10
Let, Blue = n
Total = 8 + 6 + 10 + n = 24 + n
n/(24 + n) = 1/7
=> 7n = 24 + n
=> 7n – n = 24
=> 6n = 24
=> n = 4
Hence, Blue = 4
Total = 24 + 4 = 28
Probability of drawing two Red balls and two Blue balls from bag A
= (8c2 x 4c2)/28c4
= (28 x 6)/20475
= 56/6825
In bag C:
Red = 9
Green = 3
Yellow = 2/3 x 9 = 6
Let, Blue = k
Total = 9 + 3 + 6 + k = 18 + k
k/(18 + k) = 1/10
=> 10k = 18 + k
=> 10k – k = 18
=> 9k = 18
=> k = 18/9
=> k = 2
Hence, Blue = 2
Total = 18 + 2 = 20
Probability of drawing two Green balls and two Yellow balls from bag C
= (3c2 x 6c2)/20c4
= (3 x 15)/4845
= 3/323
Required percentage = [(56/6825)/(3/323)] x 100
= 88.34%
= 88% approx.
7) Answer: c)
In bag B:
Red = 4
Green = 5
Let, Yellow = n
And Blue = k
Total = 4 + 5 + n + k = 9 + n + k
n/(9 + n + k) = 1/6
=> 6n = 9 + n + k
=> 6n – n – k = 9
=> 5n – k = 9 ———– (i)
And
4/(9 + n + k) = 2/9
=> 36 = 18 + 2n + 2k
=> 2n + 2k = 36 – 18
=> 2n + 2k = 18
=> n + k = 9 ————- (ii)
Adding (i) and (ii)
5n – k + n + k = 9 + 9
=> 6n = 18
=> n = 3
From (ii)
3 + k = 9
=> k = 9 – 3
=> k = 6
Hence, Yellow = 3
Blue = 6
Total = 9 + 3 + 6 = 18
In bag E:
Red = 6
Green = 4
Yellow = 4/3 x 6 = 8
Let, Blue = m
Total = 6 + 4 + 8 + m = 18 + m
m/(18 + m) = 2/11
=> 11m = 36 + 2m
=> 11m – 2m = 36
=> 9m = 36
=> m = 4
Hence, Blue = 4
Total = 18 + 4 = 22
Required ratio = 18 : 22 = 9 : 11
8) Answer: c)
Red = 3
Green = 7
Let, Yellow = n
And Blue = k
Total = 3 + 7 + n + k = 10 + n + k
k/(10 + n + k) = 3/10
=> 10k = 30 + 3n + 3k
=> 10k – 3k – 3n = 30
=> 7k – 3n = 30 ——— (i)
n/(10 + n + k) = 1/5
=> 5n = 10 + n + k
=> 5n – n – k = 10
=> 4n – k = 10 ————- (ii)
Equation (i) + 7 x equation (ii)
7k – 3n + 28n – 7k = 30 + 70
=> 25n = 100
=> n = 4
From (ii)
4 x 4 – k = 10
=> k = 16 – 10
=> k = 6
Hence, Yellow = 4
Blue = 6
Total= 10 + 4 + 6 = 20
Probability of drawing four balls from bag D such that all the balls are of different colour
= (3c1 x 7c1 x 4c1 x 6c1)/20c4
= (3 x 7 x 4 x 6)/4845
= 504/4845
Probability of drawing four balls from bag D such that all the balls are of same colour
= (7c4 +4c4 +6c4)/20c4
= (35 + 1 + 15)/4845
= 51/4845
Required sum = 504/4845 + 51/4845
= (504 + 51)/4845
= 555/4845
= 37/323
9) Answer: a)
Quantity I:
Red = 9
Green = 3
Yellow = 2/3 x 9 = 6
Let, Blue = n
Total = 9 + 3 + 6 + n = 18 + n
6/(18 + n) = ¼
=> 24 = 18 + n
=> n = 24 – 18
=> n = 6
Hence, Blue = 6
Total = 18 + 6 = 24
Required probability = (9c2 x 3c1 x 6c1)/24c4
= (36 x 3 x 6)/10626
= 108/1771
Quantity II:
Red = 6
Green = 4
Yellow = 4/3 x 6 = 8
Let, Blue = k
Total = 6 + 4 + 8 + k = 18 + k
4/(18 + k) = 2/11
=> 2/(18 + k) = 1/11
=> 22 = 18 + k
=> k = 22 – 18
=> k = 4
Hence, Blue = 4
Total = 18 + 4 = 22
Required probability = (6c1 x 4c1 x 4c2)/22c4
= (6 x 4 x 6)/7315
= 144/7315
Hence, Quantity I > Quantity II
10) Answer: c)
Red = 5
Green = 8
Let, yellow = n
And Blue = k
Total = 5 + 8 + n + k = 13 + n + k
From I:
5/(13 + n + k) = ¼
=> 20 = 13 + n + k
=> n + k = 20 – 13
=> n + k = 7 ———— (i)
n/(13 + n + k) = 3/20
=> 20n = 39 + 3n + 3k
=> 20n – 3n – 3k = 39
=> 17n – 3k = 39 ————- (ii)
Equation (i) x 3 + Equation (ii)
3n + 3k + 17n – 3k = 21 + 39
=> 20n = 60
=> n = 3
From (i)
3 + k = 7
=> k = 7 – 3
=> k = 4
Hence, Yellow = 3
Blue = 4
Total = 13 + 3 + 4 = 20
Required probability = (8c2 x 4c2)/20c4
= (28 x 6)/4845
= 56/1615
From II:
8/(13 + n + k) = 2/5
=> 4/(13 + n + k) = 1/5
=> 20 = 13 + n + k
=> n + k = 20 – 13
=> n + k = 7 ———– (iii)
k/(13 + n + k) = 1/5
=> 5k = 13 + n + k
=> 5k – k – n = 13
=> 4k – n = 13 ——— (iv)
Equation (iii) + Equation (iv)
n + k + 4k – n = 7 + 13
=> 5k = 20
=> k = 4
From (iii)
n + 4 = 7
=> n = 7 – 4
=> n = 3
Hence, Yellow = 3
Blue = 4
Total = 13 + 3 + 4 = 20
Required probability = (8c2 x 4c2)/20c4
= (28 x 6)/4845
= 56/1615
Hence, either statement I alone or statement II alone is sufficient to answer the question.





